Welcome to Ask Us Whatever. I’m your host, Joe Sorge.
So, let’s take the next step and describe how motion can change our perception of a sequence of events. Again, we’ll use sound to illustrate the concepts before moving on to light and special relativity.
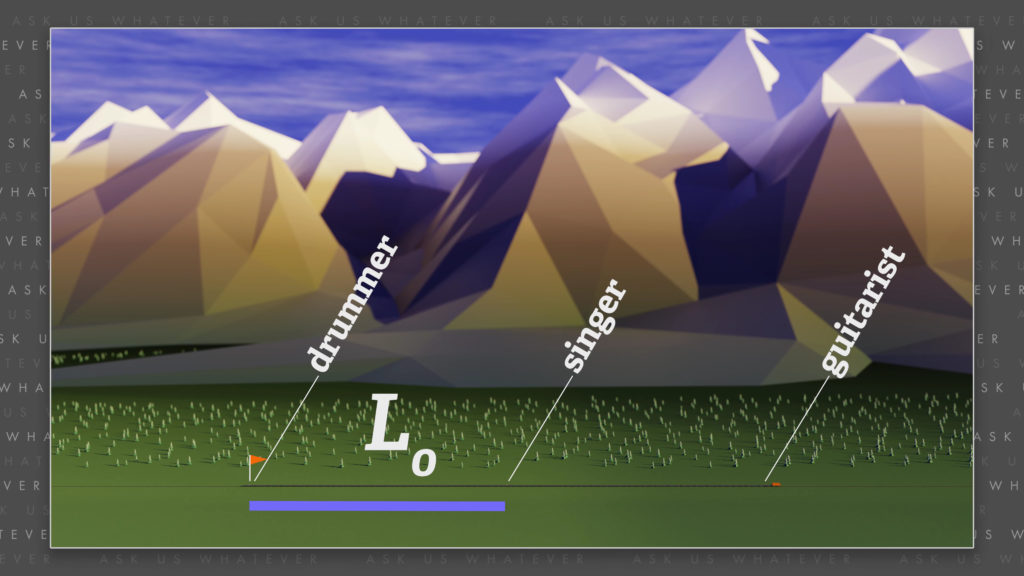
Let’s assume a band wants to perform on a train driving through the countryside; but all they can find is an empty platform train almost a half mile long.

They decide it would be cool to set up along the length of the train, so they position the drummer at the very back of the train, the guitarist at the very front of the train, and the singer in the middle.
The train happens to be 2250 feet long, which if you do some quick math, quite fortunately, is the speed of sound times 2 seconds. In other words, it would take 2 seconds for sound to travel from the back of the train to the front of the train, or the other way around. And it would take 1 second for sound to travel from the singer in the middle of the train to the musicians on the end.
Now before the train leaves the freight yard, they practice a song. The singer shouts into her microphone, “one, two; one two three four” but she doesn’t hear any music from the musicians for about 2 seconds after the downbeat.

So, she calls them on their cell phones, and they explain that they played their parts as soon as they heard her call out the downbeat.

The drummer thinks well, maybe the delays due to the long distances between them, and asks that they all synchronize their smartphone stopwatches and start playing as soon as the stopwatches reach the 1-minute mark. So, they all click their start buttons when the singer gives a hand signal.

(Keep in mind that they have the benefit of a means of communication that travels faster than sound to perform this synchronization. Later, when we talk about the speed of light, we won’t have the luxury, and that will make a big impact on synchronization.)
Now, with their stopwatches synchronized, they all begin to play at the one-minute mark, and this time the music reaches the singer one second late, instead of two seconds late.

Ugh. They next decide that the drummer and the guitarist, instead starting at the same time as the singer, they should begin playing when their stopwatches hit the 59 second mark. This will allow their music a full second to travel the 1125 feet to the singer.

This time everything works well. The solution to offset their start times, or in essence offset their clocks, made up for the time it took for sound to travel from the front and back of the train to the middle.

But then, as they’re still playing a song, the train leaves the freight yard and gradually picks up speed. And the singer begins to notice that something’s not right with the music.

The guitarist, who’s at the front of the train, seems to be playing his notes a little ahead of the beat; and the drummer, who is at the back of the train, seems to be playing a bit behind the beat. Since our drummer watched Episode 1, he calls the train’s engineer to find out how fast they are traveling: 76.7 miles per hour exactly one tenth of the speed of sound!

Again, how fortunate for our upcoming calculations.
Having taken a physics course in school, the drummer knows that sound travels at its own speed through stationary air, at 767 miles per hour, regardless of the speed at which the sound source is moving.
Now, if the train cars were enclosed, then the air inside the train would be moving with the train, and sound would travel at 767 miles per hour in either direction. But since our musicians are on an open-air flat-car train, the speed of the train will cause them to encounter the sound at different relative speeds.
The drummer reasons that the singer is moving toward the guitar sounds and away from the drum sounds; and this is causing the singer to encounter the guitar sounds before the drum sounds. But he’s not sure how to calculate the adjustments needed to cause the drum and guitar sounds to reach the singer simultaneously. So, he asked us to solve the problem for him. You know, “Ask Us Whatever.”

So, we know that the drummer should start playing slightly before the guitarist, and both musicians should start playing before the singer expects to hear the music. But, how far ahead of the guitarist should the drummer begin? Let’s start by trying to calculate the distance the train moves while sound is traveling from the drummer to the singer. And we’ll call that distance \(d\).

First let’s convert 76.7 miles per hour into 112.5 feet per second.
\(76.7\text{ mph} = 112.5 \text{ ft/s}\)
Little \(d\) will be equal to the speed of the train, which we will call little \(v\), for velocity, multiplied by the travel time for the drum sounds, which we will call little \(t\), for time.
\(d = v \times t = 112.5\text{ ft/sec} \times t \text{ seconds}\)
We know the train’s speed, but we do not know the time or the distance yet. We have what’s called one equation with two unknowns. If we can find \(d\), then we can solve for \(t\), which will be the time delay for sound to travel from the drummer to the singer. We can get there by finding another equation with distance and time in it.
Let’s call the static distance between the drummer and the singer, \(L_0\); which, in our thought experiment is half the length of the train, or 1125 feet; which just so happens to be the distance that sound travels in stationary air in one second.
While the drummer’s sound is traveling the distance Lo, the singer moves away from the oncoming sound waves, because of the movement of the train. The sound will eventually catch the singer; but it will travel the extra distance the train moves, d, before it reaches the singer.
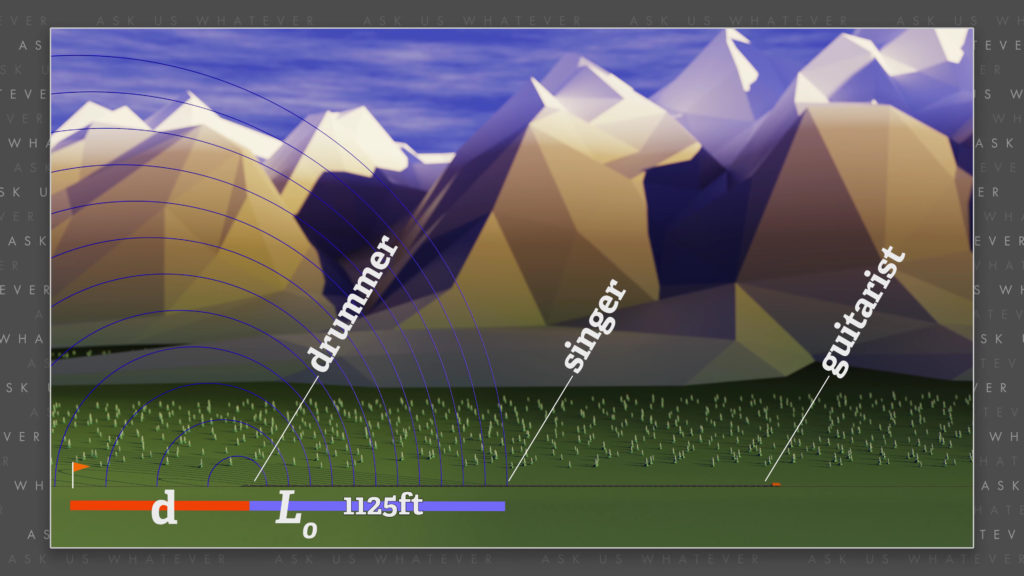
Since we know the speed of sound, which we’ll call “\(c\)”, so that our equations will be the same when we apply this all to light, we can say that:
\(L_{0}+d=t\times c \)
That is, the total distance that the sound travels between the drummer and the singer equals the static distance between the drummer and the singer, Lo, plus the distance the train and singer move, d, while the sound is chasing the singer. And this total distance will equal the ground speed of sound in stationary air, \(c\), multiplied by the time it takes sound to catch the singer. Now, we can combine the two equations. So, we can replace “\(d\)” in this second equation with \(t\times v\), from the first equation.
\(L_0 + t \times v = t \times c\)
This combined equation has only one unknown, “\(t\)”, which is what we are trying to compute. We know \(L_0\), we know \(v\), we know \(c\). So, we can rearrange the equation to solve for the time it takes the drum sounds to travel from the drummer to the singer.
First, we can subtract \(t \times v \) from both sides of the equation. So,
\(L_0 = t \times c – t \times v\)
Then we can rewrite the right side of the equation to show that t is being multiplied by both c and negative v.
\(L_0 = t (c-v)\).
Then we can divide both sides of the equation by the quantity \((c-v)\).
\(\frac{L_0}{(c-v)} = t \)
And we learn that the time it takes for sound to travel from the drummer to the singer equals the distance between the drummer and singer, \(L_0\), divided by the speed of sound minus the speed of the train.
Another way to envision this is if the singer could see the drum sounds approaching her, like in a car chase.

The drum sounds would be closing in on her at a speed equal to the speed of sound minus the speed at which she’s retreating from the sound waves.
Similar reasoning can be used to compute the time required for guitar sounds to travel from the guitarist to the singer. But now, the speed of the train causes the singer to move toward the guitar sounds, instead of away.

After performing similar math, we’ll find that the time it takes for guitar sounds to travel from the guitarist to the singer is:
\(\frac{L_0}{(c+v)} = t \)
which is the distance between them, \(L_0\), divided by the ground speed of sound plus the speed of the train, which is the speed at which the singer approaches the guitar sounds. It’s like a head on collision instead of a car chase. The guitar sounds reach the singer sooner, because the singer is moving toward the oncoming guitar sounds.

You know, just as an aside, there will be no primary Doppler effect between the three musicians here. In Episode 1, our observer experienced a change in pitch and a change in tempo because the observer was moving away from the band. Here, the musicians are not moving away or toward each other. So, even though the drummer’s sound waves will compress as he moves in the direction of the movement of the waves, the singer will be moving away from those compressed waves, which will perfectly reverse the compression.

And the guitarist’s sound waves will expand as the guitarist moves away from them, because the guitarist will be moving away from the direction of the waves that are heading toward the singer; but the waves will recompress perfectly as the singer collides with them head on.

Of course, listeners on the ground will hear the Doppler effect from all three musicians, thus making this musical thought experiment totally ridiculous. The difference is that the musicians will be in motion relative to the listeners on the ground.

And so, the listeners on the ground will hear the pitch and tempo from each performer change from high and fast, to slow and low as each performer passes them. Unfortunately, our musicians didn’t think of this, and so we’re going to renegotiate their contract when this thought experiment ends.

Nevertheless, since simultaneity is critical to understanding special relativity, let’s carry on and compute the adjustments the drummer and guitarist will need to make to their stopwatches in order for their sounds to reach the singer simultaneously. Okay, so the guitarist’s clock needs to be delayed relative to the drummer’s clock; that is, display an earlier time than the drummer’s clock. And both of their clocks need to be pushed ahead of the time displayed on the singer’s clock, so that their sounds will begin to travel toward the singer before the singer is ready to hear them.
If we insert some real numbers into these equations, we’ll find that the time, t, for sound to travel from the drummer to the singer
\(=\frac{L_0}{(c-v)} \\= \frac{1125 feet} { (1125 ft/s – 112.5 ft/s)} \\= 1.11111… seconds \)
is equal to 1125 feet, the static distance between them, divided by 1125 feet per second minus 112.5 feet per second, the latter being the speed of the train in feet per second. So, the resulting time is 1.1111… seconds.
Recall that it was only 1 second when the train was not moving. The movement of the train, which is traveling at about 10% the speed of sound, is causing it to take about 11% longer for the sound to travel from the drummer to the singer. The time required for sound to travel from the guitarist to the singer is
\(t =\frac{L_0}{(c-v)} \\= \frac{1125 feet} { (1125 +112.5)} \\= 0.909090… seconds \)
1125 feet, divided by 1125 feet per second plus 112.5 feet per second. The resulting time is .90909… seconds. Again, this was 1 second when the train was not moving. The movement of the train is causing it to take about 10% less time for the sound to travel from the guitarist to the singer. Let’s add these two numbers together.
\(\text{Total time that sound travels} \\= 1.11111 + 0.90909 \\= 2.02020 \text{ seconds (rounded)}\)
1.1111 seconds plus 0.90909 seconds equals about 2.0202 seconds. Now, that’s interesting. It takes more than 2 seconds combined for both sounds to reach the singer. When the train wasn’t moving, it took just 2 seconds. But when the train is moving at about 10% the speed of sound, the total time for the sound to reach the singer is about 1% greater than the 2 seconds. I don’t know how your brain works, but mine would not have suspected this without doing the math.
So, let’s think about it like this. In the first second, the drum sounds travel the static distance, \(L_0\), between the drummer and the singer.

But in that second, the train and the singer move away from those sounds. In our example, the train’s moving at 10% the speed of sound, so the singer will have moved 10% of the distance that sound travels in that one second.

At this point, it will require another tenth of a second for the sound to reach the singer, or 1.1 seconds in total. But in that tenth of a second, the train and singer move another one-hundredth of the distance that sound would travel in one second.

And so, it will require another hundredth of a second to reach the singer. The total time is now 1.11 seconds. And, yet, the sound has still not reached the singer, because the singer and the train moved one thousandth the distance that sound travels in one second, and so on.

According to the Greek philosopher, Zeno, the sound should never reach the singer because the singer moves one tenth of the prior movement in each iteration. The time required should be 1.111111… seconds, with the ones going on forever—unless, of course, there is a unit of length that can never be divided, but we’ll save that for a different video series.
Similar things happen with the guitar sound.

After 0.9 seconds, the guitarist’s sound has traveled 90% of the original distance between him and the singer. And the singer has moved 9% closer to the guitarist’s original position in those 0.9 seconds. But, there is still a 1% gap.

And so, it takes almost another one-one-hundredth of a second to close the gap. So, instead of it taking 90% of the original time for the guitarist’s sound to reach the singer, it takes about 90.909%, or 0.90909 seconds.

The drum sounds took 11% longer to reach the singer, while only 10% of time was saved when the guitar sounds traveled to the singer. Essentially the drum sounds traveled relatively slow, for a longer time, and the guitar sounds traveled relatively fast for a shorter time. So, the weighted total time is longer.
We can also compute the amount of time that the drummer needs to set his clock ahead of the guitarist’s clock.
It will be the drummer’s 1.1111 seconds minus the guitarist’s 0.90909 seconds.

That is, the offset time is the longer time required for the drum sounds to reach the singer, minus the shorter time for the guitar sounds to reach the singer. And that turns out to be 0.20202 seconds.
\(1.1111 sec- 0.90909sec \\= 0.20202sec \)
This is how much the guitarist will need to set his watch back compared to the drummer’s watch. And if the drummer’s clock is set 1.1111 seconds ahead of the singer’s clock, both sounds will reach the singer at the same time. Voila.
Okay, they’re a couple of take-home messages here. First, simultaneity is different for different observers. In order for the drum and guitar sounds to reach the singer simultaneously, the drummer and guitarist had to offset their clocks by different amounts. What the singer hears as simultaneous music, is not simultaneous at other locations on the train, or on the ground. So, clocks need to be adjusted differently to accomplish simultaneity.
The second take home message is that when the train’s velocity equals 10% the speed of sound, the total sound-travel time is 1% longer on the moving train than on the stationary train. If the train were moving at 50% the speed of sound, the additional sound travel time would have been 33% longer. If we add the two equations that we used to compute the forward and back sound-travel times:
Total time \(t= \frac{L_0}{(c-v)}+\frac{L_0}{(c+v)} \)
and do some rearranging, we learn that the total sound travel-time for a moving train is equal to:
Total time \(t = \frac{2L_0}{c\text{ } \left(1-\frac{v^2}{c^2}\right)} \)
The length of the train, 2 times \(L_0\), divided by the speed of sound; all multiplied by the quantity, 1 divided by the quantity 1 minus the speed of the train squared over the speed of sound squared.
If the train is not moving, \(v = 0\), and this equation simplifies to:
Total time \(t = \frac{2 L_0}{c}\)
which is the two seconds that we mentioned earlier. But when the train is moving, the extra term,
\(1 –\frac{v^2}{c^2} \)
adds another 2 one-hundredths of a second to the time at 10% the speed of sound and 66 one hundredths of a second at 50% the speed of sound.
We’ll learn in the next episode that this crazy ratio is very important in special relativity. It’s called the Lorentz factor. Actually, what we’re showing is the Lorentz factor squared and it appears in all types of relationships in special relativity. But for mysterious reasons, the Lorentz factor utilizes a strange square root difference in the denominator.
Lorentz Factor in Special Relativity = \(\frac{1}{1-\sqrt{\frac{v^2}{c^2}}}\)
This square root difference led to one of the greatest scientific debates regarding the nature of light, space, and time itself in the early 1900’s, and provided the groundwork for Albert Einstein to propose his special theory of relativity.
Please join us for Episode 3, where we’ll explore the mysteries surrounding this great debate, and the proposed solutions: time dilation and length contraction.
Thanks for watching.