Hey! Welcome to Ask Us Whatever. I’m Joe Sorge.
Well, this episode is on the Twin Paradox, which you’ll see, really isn’t a paradox. It arose from the writings of Paul Langevin in 1911, based on a paragraph that Einstein teased us with in 1905. Einstein wrote:
“If at the points A and B of K there are stationary clocks which, viewed in the stationary system, are synchronous; and if the clock at A is moved with the velocity v along the line AB to B, then on its arrival at B the two clocks no longer synchronize, but the clock moved from A to B lags behind the other which has remained at B by ½ t \(v^2/c^2 \) (up to magnitudes of fourth and higher order), t being the time occupied in the journey from A to B.”

And this started a debate about the slowing of the clocks that are in motion.
In 1911 Paul Langevin wrote:
“Imagine a laboratory at rest relative to the Earth, the movement of which may be considered a uniform translation, and in the laboratory two perfectly identical samples of radium. Our knowledge of the spontaneous evolution of radioactive material allows us to state that, if the 2 samples stay in the laboratory, they will lose their activity in the same way in the course of time and retain constantly equal activities. But now let us send one of the samples away from the laboratory at high speed and then bring it back. This requires that, at least at certain moments, the sample was accelerated. We can therefore state that, on return, its proper time between the beginning and the end of its excursion being less than the time between the same events seen by an observer at rest in the laboratory, it will have evolved less than the other sample and in consequence will be more active; it will have aged less having moved about in a more vigorous way.”

Langevin made two assumptions that Einstein did not make. The first assumption was that the slowing of clocks also applied to the decay of atoms. Subsequent experiments have shown this to be true.
But it wasn’t long after 1911 that speculation began on whether atomic decay rates might also apply to the aging of people.
Speculators postulated that instead of two radium samples, there were two twins; and one of them traveled in a spaceship at high speed and then returned. They postulated that the traveler would have aged less than the twin who remained at home.
I’m not going to comment on whether atomic decay rates and chemical aging reactions rely on the same principles. They may or they may not. I’m just going to clear up some physics misconceptions for now.
So, before we get into the analysis, let’s also consider Langevin’s second assumption, because it’s often used to cover up problems in logic.
“… it [the accelerated radium sample] will have evolved less than the other sample and in consequence will be more active; it will have aged less having moved about in a more vigorous way.”
Now here, Langevin was trying to cover up for one of the crazy notions of Special Relativity theory – the presumed symmetry of the Lorentz transformations.
That is, the notion that if observers in the laboratory viewed the “high speed” radium sample to move over a given path, then, an observer traveling together with the “high speed” radium sample might consider his or her own frame of reference as stationary, and propose instead, that the laboratory traveled at high speed over a symmetrical path.
I know that sounds silly, but the Lorentz transformations and Special Relativity demand that that second scenario has weight. This gets to the heart of the “paradox” of the twin paradox.

That is, if the twin who traveled in the spaceship considered the spaceship’s frame to be stationary, then wouldn’t the twin who remained on the Earth be considered the one who was in rapid motion and, therefore, the one who ages less?
This question has led to countless debates followed by countless erroneous explanations.
Sorry, I just need to chuckle… because it reminds me of a tale about a village fool and a village wise man.
One day a village fool butters a piece of bread on one side and then drops it on the floor. The bread lands with the butter side facing upward and so the fool is able to blow away the dust from the unbuttered side and eat the bread. The villagers ask the village wise man why the bread landed butter side up? Nothing ever goes well for the fool, right? Have the gods changed their opinion of him? Is he no longer a fool? The village wise man thinks for a minute and then says, “Aha. The fool is still a fool, he just buttered the wrong side of the bread!”

Explanations of the twin paradox, as printed in physics textbooks, are a lot like that story. The false premise underlying the village story is that the gods will always cause the fool to do everything wrong. The joke is that the wise man runs with this false premise and arrives at a superficially satisfying answer that does not offend the gods in the eyes of the villagers.
Well, similarly, physics textbooks conjure up a superficially satisfying explanation for differential aging between the twins. And they do so, as did Langevin in 1911, by deeming one of the participants as stationary and the other as undergoing acceleration and deceleration.
Just as the wise man chose one side of the bread to be the wrong side of the bread, the gods of physics deem one of the twins to be the unaccelerated and the other to be the accelerated.
Yet when physics professors are confronted with the mathematical symmetry of the Special Relativity theory, which requires that either twin can be deemed either accelerated or unaccelerated, they waive away the question by claiming that you don’t understand Special Relativity and will never succeed as a physicist.

Hah! Don’t be bullied! What’s going on, is that they themselves don’t really understand Special Relativity!
So, I’m going to set the record straight, hopefully once and for all.
Alright! First of all, as I’ve said many times, Special Relativity is flawed. That’s what’s tripping everyone up. The symmetry of the Lorentz transformations is simply a mathematical fantasy. Those transformations, as incorporated into Special Relativity, do not describe the universe we live in.
Let’s instead imagine that everything moving with respect to a universal, preferred reference frame, which for simplicity we will just call “space”.
It may be filled with an electromagnetic field or a Higgs field or an infinite array of invisible Eric Cartman dolls – it doesn’t matter. What matters is that the universe essentially has its own “stationary system of coordinates”, which we’ve jokingly referred to in other episodes as the cosmic train station.
And therefore, all speeds can and should be measured with respect to that coordinate system.
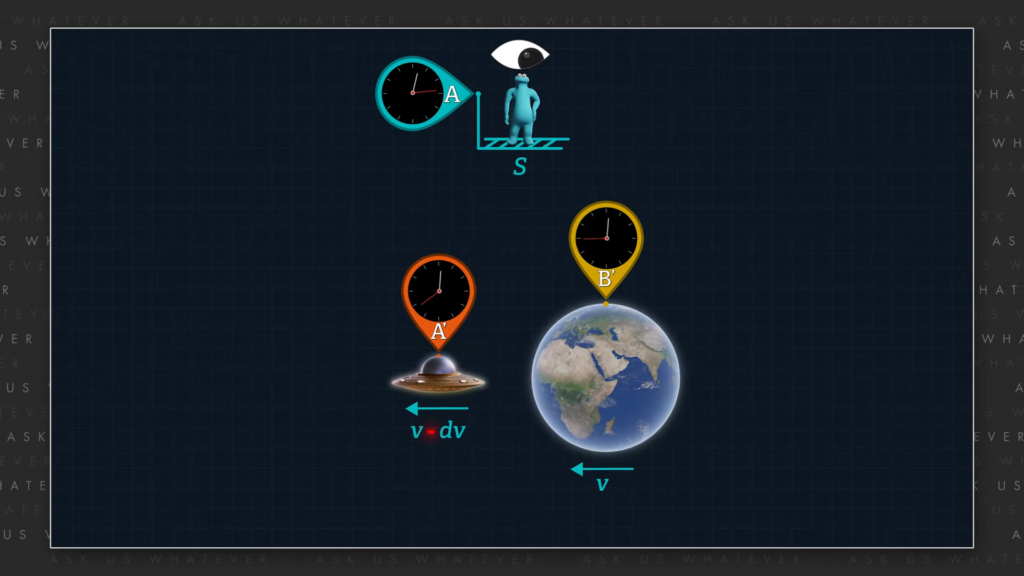
For example, suppose that the twin who remained on the Earth, and the Earth itself, move at speed v through space.
Some believe that our solar system moves through the universe in a certain direction relative to the cosmic background radiation, and that the dipole that has been detected experimentally in this signal represents a Doppler effect caused by the Earth’s motion through space.
So, if we consider that, then the twin who remains on the Earth is not stationary, but moves through space at the speed of the Earth which we’ve called v.
We’ll say that the other twin who is in the spaceship also moves relative to space, but at a speed we’ll call u.
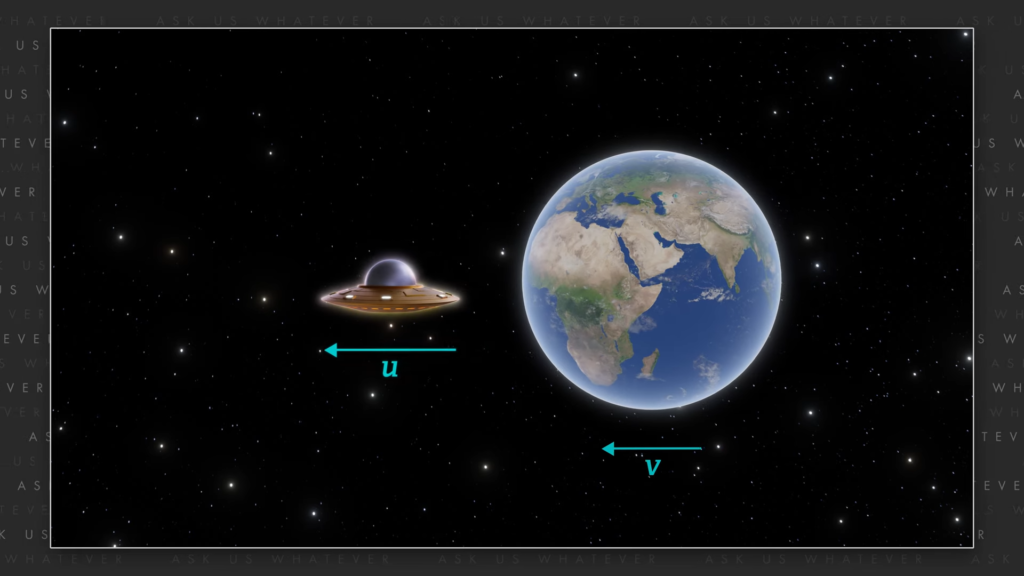
Note that both twins may experience acceleration and/or deceleration.
They may also experience differential gravity. We will come back to these concepts in a later episode, but for now let’s isolate our analysis to the underlying concept of the twin paradox: the effect of motion through space.
According to Einstein’s Special Relativity, as adapted to our concept of space, the clocks moving with the Earth will beat slower than clocks in our imaginary cosmic train station, and this slowing of Earth-bound clock rates will be a function of the speed v of the Earth through space, according to the formula, dt, which is a time that elapses on a clock that’s stationary in the cosmic train station, multiplied by the square root of one minus v squared over c squared.
\({dt^\prime}_{Earth}={dt}_{space}\times\sqrt{1-\frac{v^2}{c^2}} \)
And a clock on a spaceship will beat slower than a clock that’s in the cosmic train station as a function of the spaceship’s speed, u, through space, according to the analogous formula, dt, which is the time elapsed on a clock in a cosmic train station, multiplied by the square root of one minus u squared over c squared.
\({dt^\prime}_{spaceship}={dt}_{space}\times\sqrt{1-\frac{u^2}{c^2}} \)
If u is greater than v, then the clocks on the spaceship will beat slower than the clocks on the Earth. But if, let’s say v is a fairly significant speed at which our solar system travels through space, and the spaceship heads in the opposite direction, then u might be less than v relative to space.
Both v and u are measured with respect to distance traveled through space in a given unit of cosmic train station clock-time. Not with respect to their speed or direction relative to each other.
If we want to ask by how much do the clocks on the Earth and the clocks in the spaceship diverge during a given amount of cosmic train station time, the answer is, the time that elapses on the clock in the cosmic train station times the quantity equaling the square root of one minus v squared over c squared minus the square root of one minus u squared over c squared.
\({dt^\prime}_{Earth}-{dt^\prime}_{spaceship}={dt}_{space}\times\left(\sqrt{1-\frac{v^2}{c^2}}-\sqrt{1-\frac{u^2}{c^2}}\right) \)
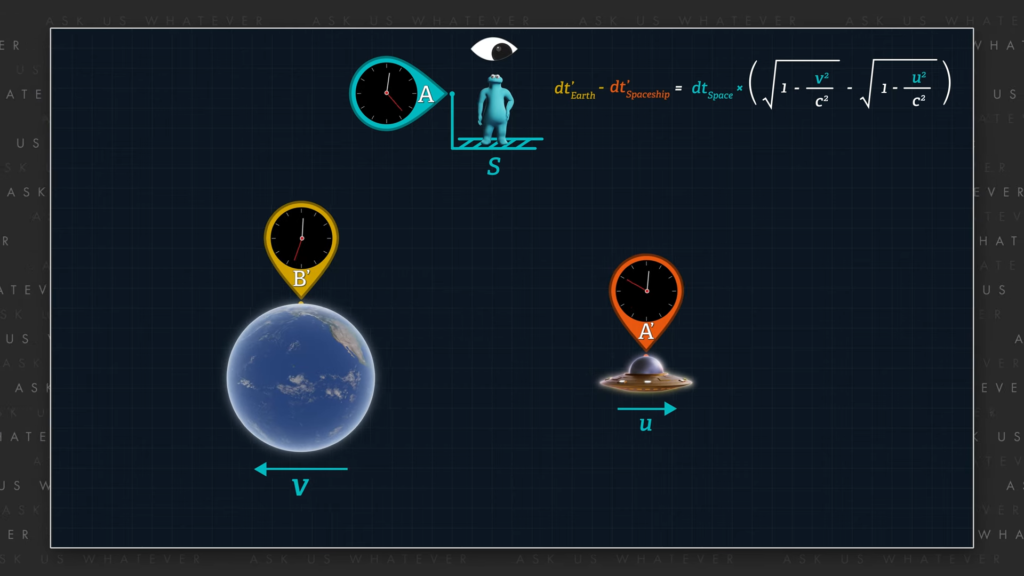
If the twin on the Earth spent 1 year traveling with the Earth at speed v through space, and the twin on the spaceship traveled during that same year at speed u through space, then this formula would describe the difference in the passage of time for the two twins. If u is greater than v, then the twin on the spaceship would experience a greater slowing of clock tick rate than the twin on the Earth, which might possibly represent a slowing of the aging process for the twin on the spaceship. But if the Earth is zipping through space and the spaceship moves in the opposite direction, causing the spaceship to move slower than the Earth through space, then the twin on the Earth would experience clocks on the Earth ticking at a slower rate than clocks on the spaceship.
Now this is fun! Textbook authors get really confused when they try to discuss the return journey for the twin on the spaceship.
They naively assume that the speed of the twin on Earth is zero and that the speed of the twin on the spaceship is u during, both, the outbound trip and the return trip.
If that’s the case, then our formula states that the spaceship clock will tick slower than the clock on a stationary Earth by the square root of one minus u squared over c squared.
\({dt^\prime}_{Earth}-{dt^\prime}_{spaceship}=2\times{dt}_{space}\times\left(\sqrt{1-\frac{0^2}{c^2}}-\sqrt{1-\frac{u^2}{c^2}}\right) \)
In other words, the twin on the spaceship will experience time passing more slowly during both the outbound and return journeys.
But what if Earth is moving at speed v through space, and the spaceship leaves the Earth and heads in the same direction at speed dv relative to the Earth?
That is, the spaceship will be moving at speed \(v + dv \) relative to space on its outbound journey, and at speed \(v – dv \) relative to space on its return journey.
It travels faster through space than Earth when heading in the same direction as Earth is moving, but slower through space when it returns to Earth. In that case the difference in clock rates would be governed by the following formula:
\({dt^\prime}_{Earth}-{dt^\prime}_{spaceship}=\)
\({dt}_{space}\times\left(2\times\sqrt{1-\frac{v^2}{c^2}}-\sqrt{1-\frac{\left(v+dv\right)^2}{c^2}}-\sqrt{1-\frac{{(v-dv)}^2}{c^2}}\right) \)
We can estimate the difference in elapsed clock time using a Taylor series expansion of the square root terms.
\({dt^\prime}_{Earth}-{dt^\prime}_{spaceship}\approx \)
\(\approx{dt}_{space}\times\left(2\times(1-\frac{v^2}{2c^2})-(1-\frac{v^2+2vdv+dv^2}{2c^2})-(1-\frac{v^2-2vdv+dv^2}{2c^2})\right) \)
Which, if we ignore the very small \(dv^2/2c^2 \) terms, we obtain, two times the speed of the Earth, v, times the speed of the spaceship relative to the Earth, dv, divided by light speed squared, all times the time elapsed on a clock that’s in the cosmic train station.
\({dt^\prime}_{Earth}-{dt^\prime}_{spaceship}\approx{dt}_{space}\times\frac{2vdv}{c^2} \)
When both v and dv are small relative to light speed c, our Taylor series expansion is quite accurate, and the difference in time is very small.
Please note that the formula shown at minute 12 in the video has an error. The solution should be \(\frac{v^2}{c^2} \), not \(\frac{2vdv}{c^2} \). The value of \(\frac{v^2}{c^2} \) is even smaller than \(\frac{2vdv}{c^2} \) which further supports the point that there will be almost no differential aging of the twins.
In other words, if the Earth is moving through space at a small fraction of speed c, which is likely, and the outbound and return trips for the twin in the spaceship are at the same speed relative to the earth, but their average speed relative to the universe is about the same as the speed at which the earth is moving through the universe (and over a relatively linear path), then the twin in the spaceship will not experience much difference in clock readings upon a return to the Earth. That is, with respect to potential aging, the returning twin should be approximately the same biological age as the twin that remained on the Earth.
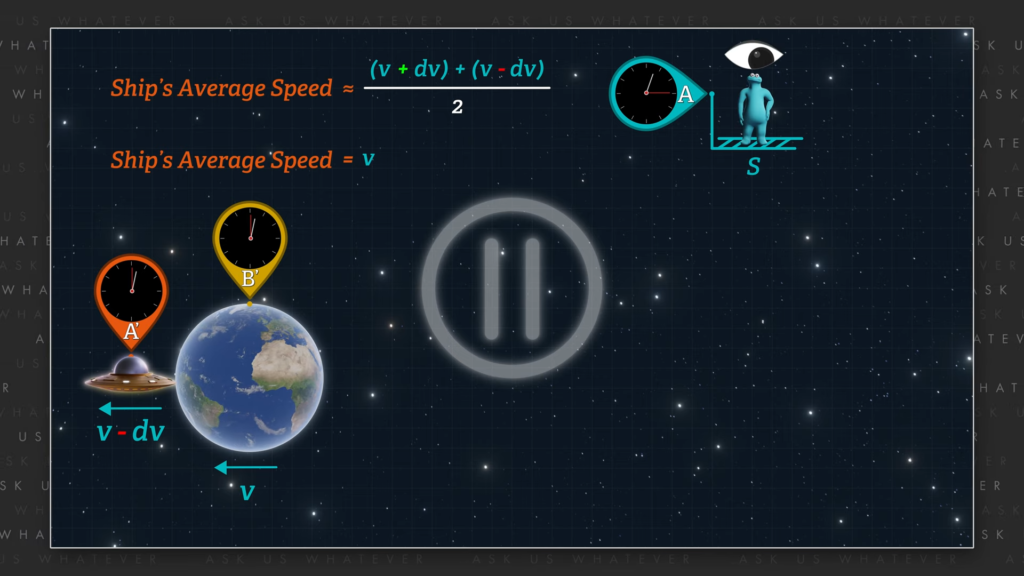
And since its most likely that the Earth is moving through space much faster than a current day spacecraft, it is most likely that a passenger on a spacecraft that makes a relatively linear trip through space and returns over approximately the same linear path will experience very little difference in the readings on the Earth-based and spaceship-based clocks at the end of the trip.
And thus, if the variable aging concept is real, the passengers on the spaceship will most likely find the people on the Earth to have aged at about the same rate as themselves. Not older!
Well, I hate to leave you with the impression that we cannot possibly slow down the aging process. Based on what I’ve presented here, there might be a way; but it means that we must identify the true, universal stationary frame of space and move relative to it. Which you might suspect is going to be the subject of an upcoming episode.
A good first step would be to determine the speed and direction of the Earth through space! I just need Elon’s help to get a few satellites launched. And this experiment that I have in mind should not only reveal the speed of the Earth through space, but might also allow us to determine whether time dilation follows the Lorentz gamma factor or the gamma(s) factor that I’ve proposed in the Alternative Model. Well worth the investment.
Okay! Before concluding, I want to once again emphasize that in this episode I’ve left out the potential effects of differences in gravity, differences in acceleration, and what might happen if the spaceship takes a non-linear journey through space. All of these might also affect the outcome which might lead to differential aging; but not in ways typically covered in the “twin paradox”.
Okay. In summary, the “twin paradox” is just a widely disseminated misunderstanding of how Special Relativity works.
Well, I hope you’ve enjoyed this episode.
And if you have any questions, please leave them in the comments section.
I’m Joe Sorge, and thanks for watching.