Welcome to Ask Us Whatever. I’m your host, Joe Sorge.
In the last episode we learned about time dilation, and why all observers believe that the speed of light is constant. And while the explanation for time dilation is a good one for clock elements that move side to side with respect to the direction of motion, something we will call “transverse motion”,
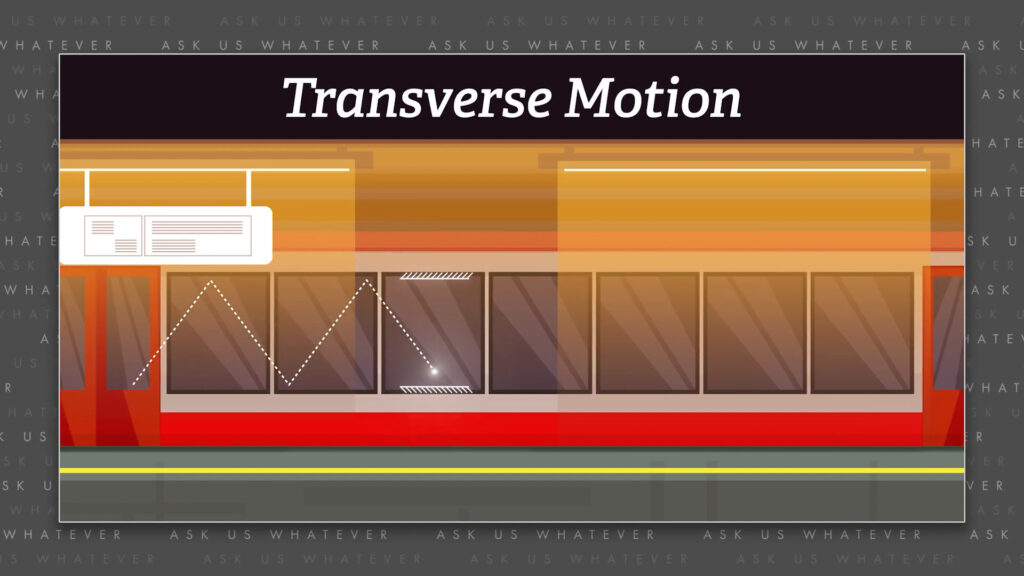
things get more complicated if clock elements move forward and backward, something we will call “longitudinal motion”.
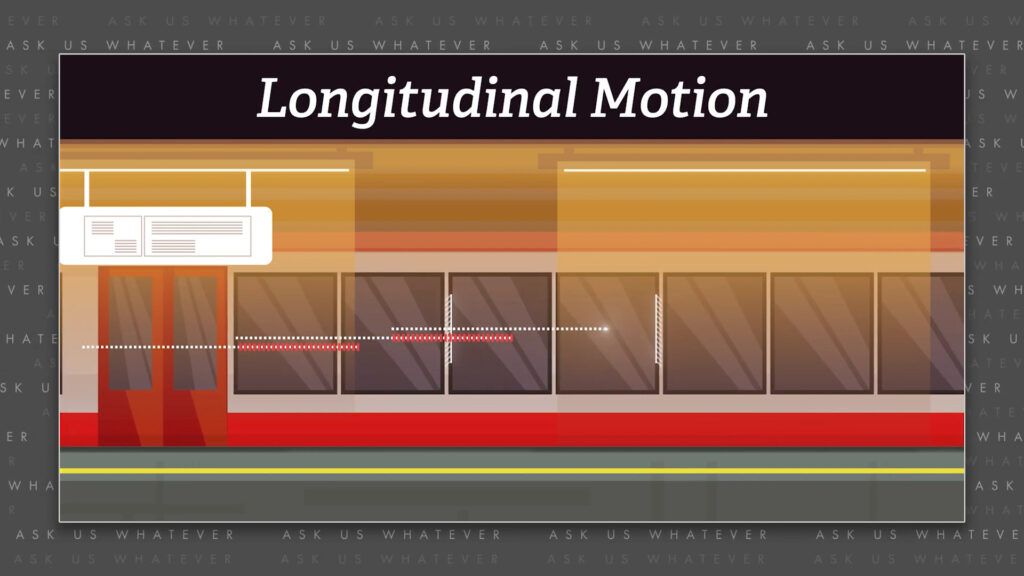
So, let’s once again talk about Einstein’s thought experiment with people on a train and people in a station. Let’s say we make a light clock that bounces light between two mirrors, but this time one is attached to the interior wall at the back of the train-car and the other is attached to the interior wall at the front of the train-car. Let’s say that the distance from the back to the front is \(L’ \) meters. Regardless of whether the train is stationary or moving, if observers on the train measure this distance, it will always appear to them to be \(L’ \) meters long. We will call this the proper length of the train.

People in the station will see things differently. As the light travels from the back of the train to the front, the front of the train moves forward. People in the station will see the forward-moving light chasing the mirror attached to the forward-moving front of the train-car.
Now, since Einstein believed that light travels at a constant speed, regardless of the speed of its source, the relative speed of light moving toward the front of the train is \(c \) stationary-frame meters per second, minus the speed of the train, which is \(v \) stationary-frame meters per second.
\(\text{Relative Speed of Light}= \)
\((c-v) \space \text{m/s} \)
Now take a moment to think about this. Even though light bounces off of a mirror on the moving train, it travels at the same speed with respect to the ground or the station as if it had bounced off of a stationary mirror.

Another example might be the light coming from the front headlight of a train. According to Einstein, light will travel at the same speed regardless of whether the train is moving or not.

This is similar to what we learned about sound in Episode 2. Its speed was determined by the air through which the sound traveled.

The sound speed did not change whether the source of the sound was moving or stationary. For light, we don’t know for certain if light travels through some type of medium or not, but 19th century scientists believed that light travels at the same speed whether the light source is moving, or stationary, or even if the source moves backwards.
This phenomenon caused scientists in the 19th century to speculate that light traveled through something they called an “ether”. Ether, for light, would be like air, for sound. It could be some type of invisible medium found in the vacuum of space through which light travels at a constant speed, regardless of the speed of the source of the light. So, they set out to try to detect the ether. The most famous experiment of this time was conducted by two scientists, Michelson and Morley.

They reasoned that light should require more time to move in the direction of the Earth’s motion compared to moving in a direction perpendicular or transverse to the direction of Earth’s motion. To understand what they expected, we need to do some math.
Now using the reasoning from the prior episode, the time required for light to travel transverse to the direction of motion is
\(t_{\text{transverse}}=\frac{\gamma h’}{c} \)
the Lorentz gamma factor times the transverse distance, which we called \(h’ \) in the last episode, divided by light speed \(c \). The Lorentz gamma factor is the ratio of the diagonal path that light travels, as seen by people in the stationary perspective, divided by \(h’ \). You can think of the Lorentz factor as a multiplier that converts the transverse distance, \(h’ \), into the diagonal distance. And when we divide the diagonal distance by light speed, we get the stationary-frame time it takes light to travel the diagonal distance.
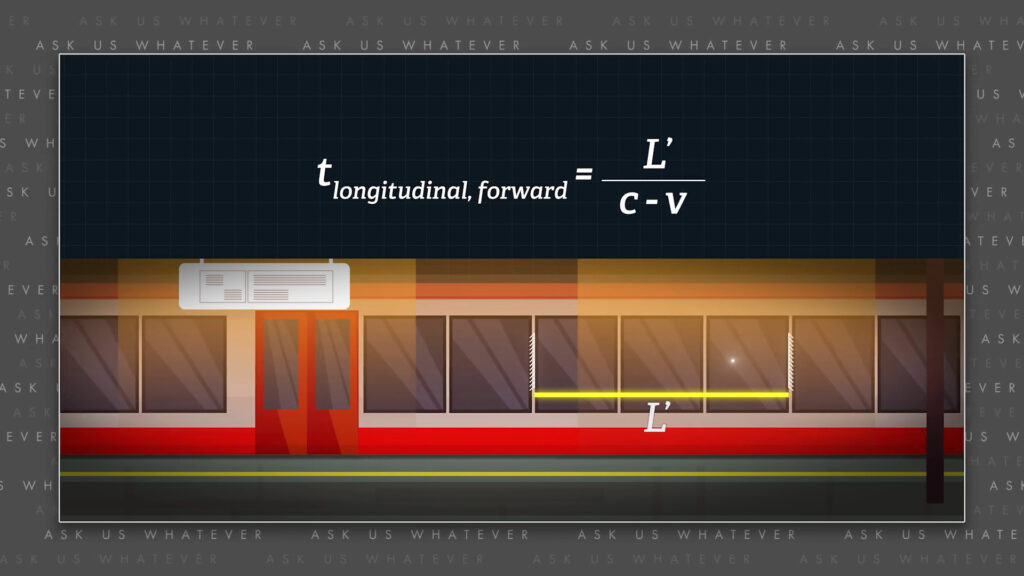
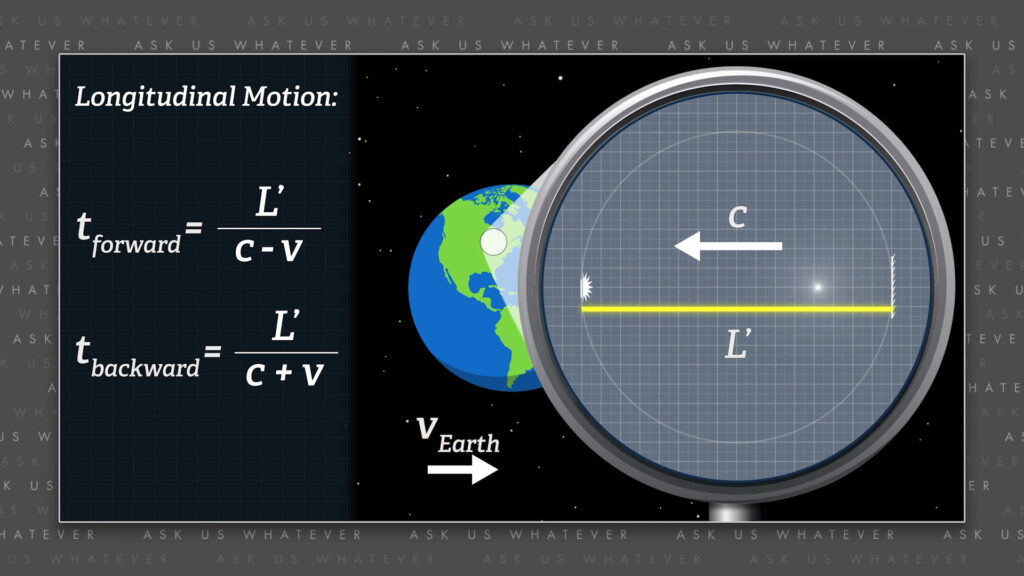
Now for light traveling the longitudinal distance from the rear to the front of the train-car and the time required from the perspective of observers in the stationary frame is,
\(t_{\text{forward}}=\frac{L’}{(c-v)} \)
the length of the train-car, \(L’ \), divided by the speed of light relative to the speed of the train, which is \(\space c \space minus \space v \).
As we discussed in Episode 2, it’s like a car chase. The front car is trying to escape but the trailing car is moving faster. The trailing car closes the gap between them at a rate equal to their relative speed, which is the speed of the faster trailing car minus the speed of the slower front car. The time required for the trailing car to catch the front car is the distance between them, \(L’ \), divided by the relative speed at which the trailing car closes the gap.

Michelson and Morley reasoned that the time required for light to travel in the direction of Earth’s motion would be the distance between the mirrors in their experimental apparatus, \(L’ \), divided by the speed of light minus the speed of the Earth moving through the ether. And similarly, they reasoned that once the light bounced back from the downstream mirror it would return in less time, which would be equal to
\(t_{\text{return}}=\frac{L’}{(c+v)} \)
the distance between the mirrors, \(L’ \), divided by light speed plus the speed of the Earth through the ether. They added the speed of the Earth because on the return trip the mirror at the origin is now traveling toward the returning light. So, the relative speed at which light returns to the origin, as seen from the stationary frame, is faster than light speed. This doesn’t mean light was traveling faster than \(c \). It means that the returning light traveled at speed \(c \) through space, but the Earth, or train, approached the returning light at speed \(v \), and so they were on a collision course at a combined speed of \(c + v \).
The total time required for light to travel from the origin to the downstream mirror, and then return back to the origin is simply the sum of both times.
\(t_{\text{total}}=t_{\text{forward}}+t_{\text{return}}= \)
\(\frac{L’}{(c-v)}+\frac{L’}{(c+v)} \)
And if we rearrange this formula using basic algebra, we learn that the total time is
\(t_{\text{total}}=\frac{2L’c}{c^{2}-v^{2}} \)
two times the distance between the mirrors, times light speed, divided by light speed squared minus the speed of the Earth squared. If we divide the numerator and denominator by \(c \space squared \), we get
\(t_{\text{total, longitudinal}}=\frac{2L’}{c(1-\frac{v^{2}}{c^{2}})}=\frac{2L’\gamma^{2}}{c} \)
two times the length of travel, times the Lorentz gamma factor squared, divided by \(c \).
Now if we compare this to the total time for transverse light to make a round trip between mirrors that are aimed perpendicular to the direction of travel, we see that
\(t_{\text{total, longitudinal}}\neq t_{\text{total, transverse}} \)
\(\frac{2L’\gamma^{2}}{c}\neq \frac{2h’\gamma}{c} \)
the longitudinal time does not equal the transverse time when \(L’ \) equals \(h’ \).
In the Michelson Morley experiment they created two light paths of equal length aimed at right angles to each other, both with downstream mirrors that reflected the light to a receiver. They placed the light paths on a turntable so that they could aim the paths in any direction with respect to the movement of the Earth. They reasoned that if they could aim one of the light paths in the direction of Earth’s motion, then the other light path would be at right angles to the direction of Earth’s motion, and they should see a difference in the time required for light to travel along the two paths.
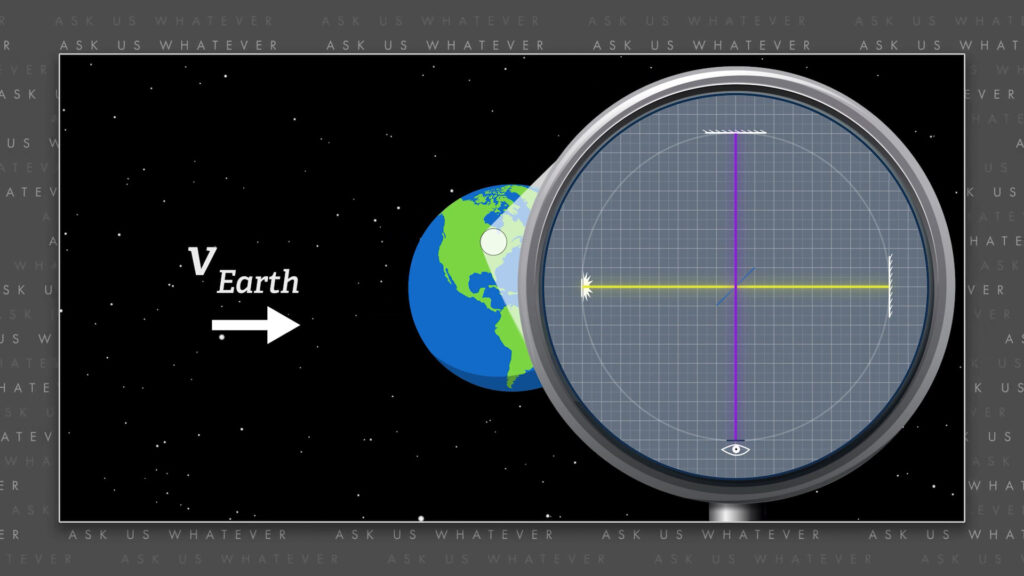
It all made a lot of sense, and they were hoping to compute the speed of the Earth through space with the results of their experiment.
Well, they were shocked by the answer. It took exactly the same amount of time for light to travel along both paths, regardless of the direction in which they oriented the turntable. They tried the experiment in the spring, the fall, the summer, the winter; during the day, at night – no matter when they performed the experiment, they never saw a difference in the time required for light to travel along the two paths. And yes, their apparatus was sensitive enough to detect a difference if one really existed. And yes, the Earth really does move through space, even though some eccentrics have claimed that the Michelson Morley result proves that the Earth is flat and the sun really does orbit the Earth.

Michelson and Morley were stymied by their result. It suggested either that there was no ether, or somehow the ether was being dragged along with the Earth as it moved through space, an idea that was eventually ruled out with further experiments. Various other explanations were offered, one of which will be the subject of the next episode, length contraction. I don’t think it’s the correct answer, but it’s the answer that has been accepted by the scientific community, and was incorporated in Einstein’s special theory of relativity. And if you’d like to see how length contraction potentially solves this mystery, then you’ll be interested in the next episode. And in the episode that follows that one, I’ll offer what I think is a better answer.
If you have any questions, please write them down in the comments section. I’m Joe Sorge, and thanks for watching.