Welcome to Ask Us Whatever. I’m your host, Joe Sorge
This episode will make a lot more sense if you’ve watched the previous episode. If not, I would suggest doing so. But if you’re already an expert on special relativity, then please, forge ahead.

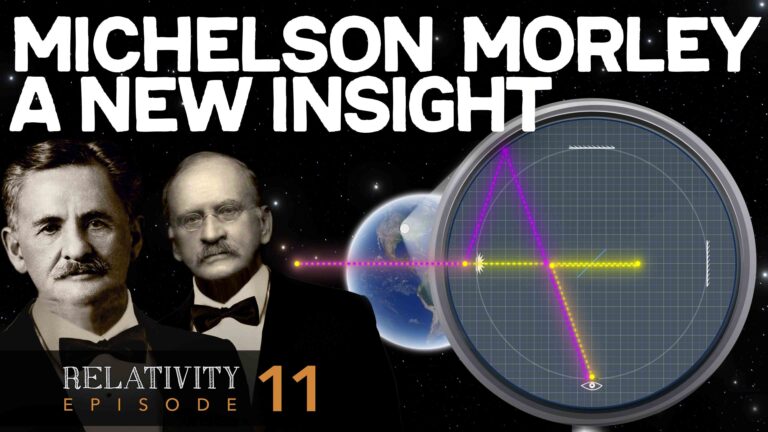
In the last episode we learned that Michelson and Morley were expecting the time required for light to travel in the direction of motion to take longer than the time required for light to travel at right angles, or transverse, to the direction of motion.
\(t_{\text{total, longitudinal}}\neq t_{\text{total, transverse}}\)
\(\frac{2L’\gamma^{2}}{c}\neq \frac{2h’\gamma}{c}\)
But that’s not what they observed. Instead, they learned that
\(t_{\text{total, longitudinal}}= t_{\text{total, transverse}}\)
the time required for light to travel longitudinally was exactly equal to the time required for light to travel transversely. This result puzzled scientists in the 19th century, because the basic math demanded that travel times be different. The longitudinal distance might appear to be the same as the transverse distance when measured by observers in the moving frame of reference,

but observers in the stationary frame of reference would see that the distances are not the same.


And this created a dilemma because it would not be possible for Michelson and Morley to witness the simultaneous return of longitudinal and transverse light beams in their laboratory unless stationary frame observers, let’s say floating out in space, would also witness the same simultaneous return. Keep in mind that events that occur at the same location along the axis of motion are seen as simultaneous in both the moving and stationary frames.
In the late 1800s, Henrik Lorentz proposed a solution to the Michelson Morley result; which is that lengths contract in the direction of motion, but not perpendicular to the direction of motion.

The concept is that moving objects actually get physically shorter along the axis of motion, including the moving observers themselves but they don’t notice the change. Moving observers will not detect the shrinking of proper lengths because their measuring devices also contract along the axis of motion. So, the contracted length of a moving train car will appear to be the same length when measured with a contracted meter stick.

The concept is similar to time dilation, where the clocks used by moving observers tick more slowly, but the moving observers are unaware of the slowing. The moving observers assume that their seconds\(’ \) are of the same duration as stationary seconds, even though stationary observers will notice that a second\(’ \) lasts gamma-times longer than a second.

Similarly, a contracted, moving meter stick is allegedly gamma-fold shorter than a stationary meter stick. Yet the contracted observers in the moving frame do not notice the contraction because their entire environment is contracted in the same dimension.

According to Lorentz’s model, when stationary observers measure contracted length of the train with uncontracted meter sticks, they will record a smaller number of stick-lengths than moving observers who unknowingly measure the contracted length of the train with contracted meter sticks.

If the length of a train car shrinks from \(L’ \) to \(L’/\gamma \), as measured with an uncontracted meter stick, then the distance that light must travel in the longitudinal dimension will require gamma fold fewer seconds. In this case,
\(t_{\text{total, longitudinal, length contracted}}= \)
\(t_{\text{total, transverse}}\)
\(\frac{2L_{c}\gamma^{2}}{c}=\frac{2L’\gamma}{c}=\frac{2h’\gamma}{c}\)
the total time for light to travel forward and back is two times the contracted length of the train car, \(L_c \), times gamma squared, divided by light speed; which is equal to two times the uncontracted length, \(L’ \), times gamma (instead of gamma squared) divided by \(c \), which is equal two times the transverse distance, \(h’ \), times gamma divided by \(c \). In other words, the stationary observer will witness light traveling gamma-fold less distance, because of length contraction, and thus will witness it taking gamma-fold less time.

And therefore, total longitudinal travel time will be the same as transverse travel time.
Frankly I think length contraction is a fanciful idea with lots of problems. And I will get into some of those problems in next episode. But it is currently taught as one of the foundational concepts of special relativity which is one of the foundational concepts of physics.
If you have any questions, please write them in the comments section. I’m Joe Sorge, and thanks for watching.