Welcome to Ask Us Whatever. I’m Joe Sorge.
In Episode 7.4 we described how observers in two different reference frames could each convince themselves that time was passing gamma times more slowly in the other observer’s frame
Our example followed Einstein’s model, in which one reference frame is stationary with respect to a stationary system of coordinates and in which all clocks report the same time of day with no clock offset; and another reference frame that moves with respect to the stationary system of coordinates, and in which clocks were offset by an amount computed using the clock offset term of the Lorentz transformations.
We explained why it would be naïve to assume that one could snap a finger and incorrectly deploy the theory of relativity to reverse the relative speeds of the frames; that is, to make the moving frame the stationary frame and to make the stationary frame the moving frame, without requiring the clocks and meter sticks of both reference frames to be recalibrated and resynchronized. And in so doing, it appeared that the inverse Lorentz transformations are pure mathematical fiction.
Some supporters of special relativity may have wondered what would have happened if we envisioned both frames moving symmetrically with respect to a third, stationary frame.
So, let’s relocate the stationary system of coordinates between frames S and S’ and associate it with a third frame that we will call S’’.
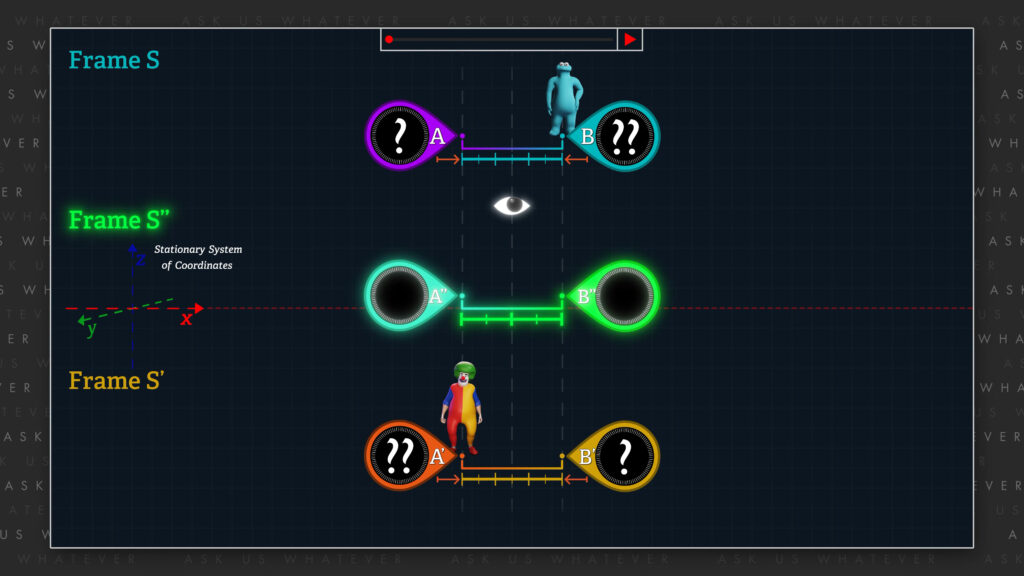
That is, a setup in which frame S’ moves in the positive x-direction with respect to the stationary system of coordinates, frame S moves at an equal but opposite speed with respect to the stationary system of coordinates, and frame S’’ remains stationary. To be consistent with Episode 7.4 we can have the relative speed of the moving frames be the same relative speed as it was in Episode 7.4, that is 0.866 times speed c.
We will now place a neutral observer in frame S’’.
So, from the perspective of the observer in frame S’’, the two moving frames would have equal-length meter sticks, their clocks would tick at the same rate, and their time-of-day readings would show equal-but-opposite spatial gradients (in other words, equal but oppositely oriented clock offsets).
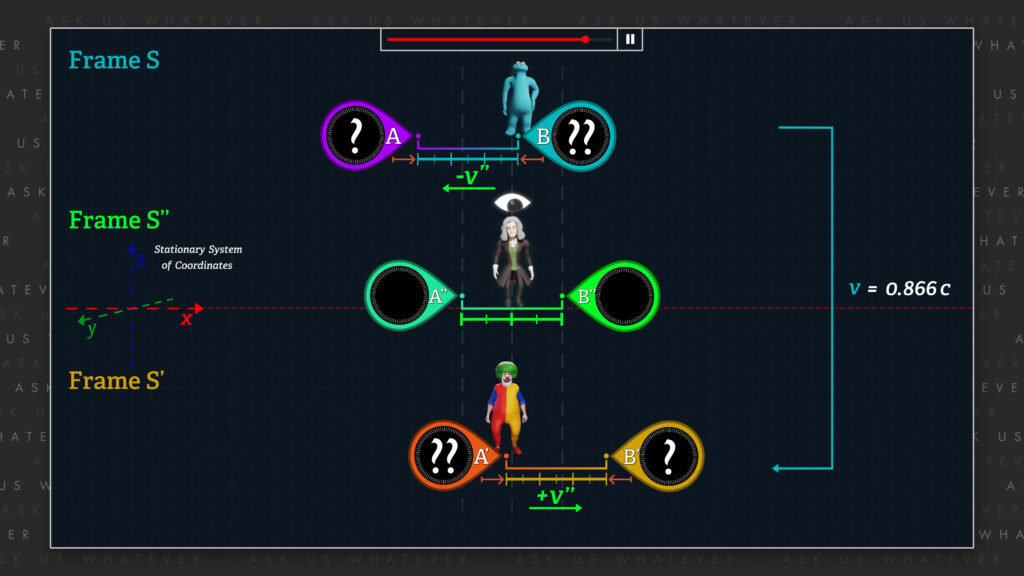
With this setup, any reversal of perspective between frames S and S’ should not require a resetting of clock offsets, time dilation, or length contraction. Observers in frames S or S’ might consider their own frame to be either moving or stationary, without requiring any physical changes within their frame, or the other moving frame. With this type of symmetry, we can eliminate most of the objections that I raised in Episode 7.4.
So, can we rescue the Lorentz transformations, and special relativity this way? The short answer is no.
Unfortunately, the relative speed between stationary frame S’’ and each of the two moving frames, is not 0.866 times speed c. As we learned in Episode 9.1, it’s not even half the original speed – it’s governed by Einstein’s non-linear velocity addition formula. This has implications for the clocks in frames S and S’. They must now be adjusted so that their tempo is dilated according to their speed relative to frame S’’ instead of relative to each other, which means that the clocks in frames S and S’ tick at the same rate, which conflicts with the rules of special relativity required in Episode 7.4.
So, we could almost skip the details and just end here, except that the details create an extremely strong case for a universal, preferred reference frame, which has huge implications for our universe. I hope that the next few minutes will demonstrate that the symmetry of the Lorentz transformations is pure mathematical fantasy, and therefore so are many of the claims of special relativity. I hope that the following analysis will convince you that special relativity is fatally flawed, and that we need to develop a model based on some type of universal, preferred frame – something like what we’ve jokingly called the cosmic train station in other episodes.
So, let’s get into it.
We will refer to the speed of frames S’ and S relative to frame S’’ as plus or minus v meters’’ per second’’, respectively. Note that the double-primed units are now considered stationary frame units.
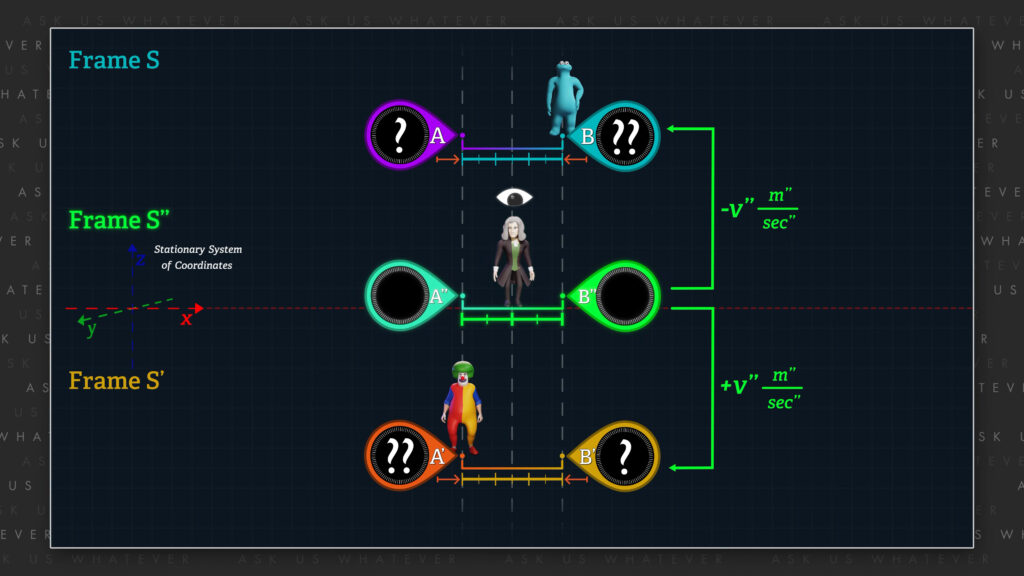
As before we will now call the speed of frame S’ relative to frame S, u meters per second, since we will now be using frame S measuring tools to measure this speed.
The velocity addition formula of special relativity computes the relative velocity, u’’, of an object moving with respect to a frame S’’ observer as, in our present setup plus v’’ all divided by 1 plus times v’’ over c-squared, where the object (for example an observer riding in frame S’) travels at speed meters per second with respect to frame S, which is moving at speed negative v’’ meters’’ per second’’ with respect to the stationary system of coordinates of frame S’’.
\(u^{\prime\prime}=\frac{u+v^{\prime\prime}}{1+\frac{uv^{\prime\prime}}{c^2}} \)
So, if frame S moves at speed negative v’’ meters’’ per second’’ with respect to the stationary system of coordinates of frame S’’, and observers in frame S observe frame S’ (the “object”) to be moving at speed u meters per second relative to frame S, then u’’ is the speed that our neutral observer in frame S’’ will observe frame S’ to be moving, as measured in the neutral observer’s units of meters’’ per second’’.
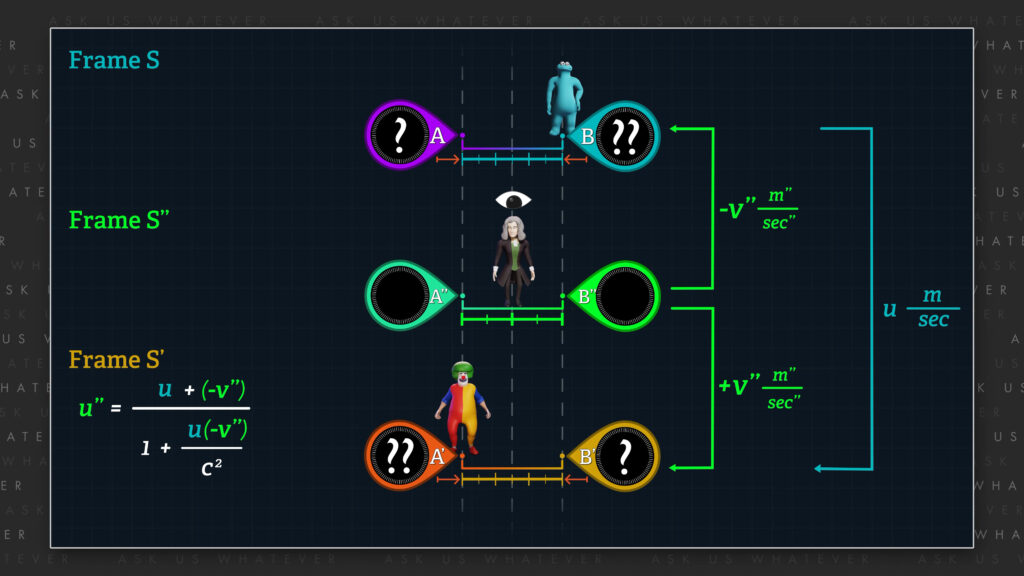
We can then write the relativistic velocity addition formula to solve for u’’, as u plus the speed of frame S relative to frame S’’, which is negative v’’, all divided by 1 plus u times negative v’’ over c squared.
\(u^{\prime\prime}=\frac{u+\left(-v^{\prime\prime}\right)}{1+\frac{u\left(-v^{\prime\prime}\right)}{c^2}} \)
And since, relative to frame S’’, frame S’ moves at an equal but opposite speed (that is, in the positive x-direction) as compared to frame S, we can substitute positive v’’ for u’’ in the velocity addition formula.
\(v^{\prime\prime}=\frac{u-v^{\prime\prime}}{1-\frac{uv^{\prime\prime}}{c^2}} \)
Rearranging with some fast algebra, produces a quadratic equation, which can be solved for v’’ using the quadratic formula.

\(v^{\prime\prime}-\frac{u{v^{\prime\prime}}^2}{c^2}=u-v^{\prime\prime} \)
\(0=\frac{u}{c^2}{v^{\prime\prime}}^2-2v^{\prime\prime}+u \)
\(v^{\prime\prime}=\frac{2\pm\sqrt{4-\frac{{4u}^2}{c^2}}}{\frac{2u}{c^2}} \)
\(v^{\prime\prime}=\frac{1\pm\sqrt{1-\frac{u^2}{c^2}}}{\frac{u}{c^2}} \)
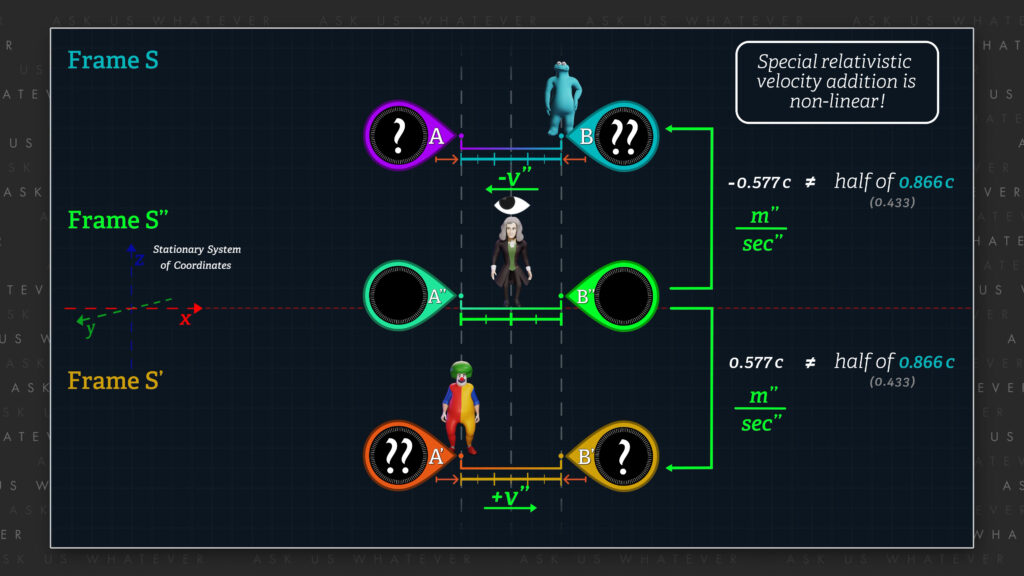
Now let’s compare this approach to the setup in Episode 7.4 where the observer in frame S observes frame S’ traveling at 0.866 times c. In other words, , the speed of frame S’ relative to frame S, would be equal to 0.866 c using the clocks and meter sticks of frame S. By selecting the negative sign in the quadratic formula for now, we find that the speeds of frames S and S’ relative to frame S’’, what we call positive v’’ equals, approximately 0.577 times c meters’’ per second’’.
\(v^{\prime\prime}=0.577\ c\ meters^{\prime\prime} per\ second^{\prime\prime} \)
That is, our stationary observer in stationary frame S’’ will perceive frame S’ as moving at speed 0.577 c in the positive x-direction relative to the stationary system of coordinates; frame S as moving at speed 0.577 c in the negative x-direction with respect to the stationary system of coordinates; and the observers in S and S’ will each perceive the other’s frame as moving at 0.866 c meters per second (or meters’ per second’), respectively, using the clocks and meter sticks of their respective frames, which are now slowed by a Lorentz gamma factor of 1.225 due to their relative speeds of 0.577 c meters’’ per second’’ relative to the neutral observer in frame S’’.
\(\gamma_L=\frac{1}{\sqrt{1-\frac{{v^{\prime\prime}}^2}{c^2}}}=\frac{1}{\sqrt{1-\frac{{0.577}^2}{1^2}}}=1.225 \)
We can immediately see that 0.577 times c is not numerically half of 0.866 times c. Special relativistic velocity addition is non-linear. And the difference in the two speeds is not explained by a simple time dilation gamma factor.
Also, in this setup, all of the screwy-ness of special relativity must still be taken into account. In other words, clocks A and A’ and B and B’ must be separated by a distance that is now proportional to the Lorentz gamma factor computed at speed v’’, not a Lorentz factor of 2 as when comparing frames S and S’ directly, in Episode 7.4.
distance separating clocks \(= \frac{1\ light\ second^{\prime}}{1.225}=0.816\ light\ seconds^{\prime\prime} \)
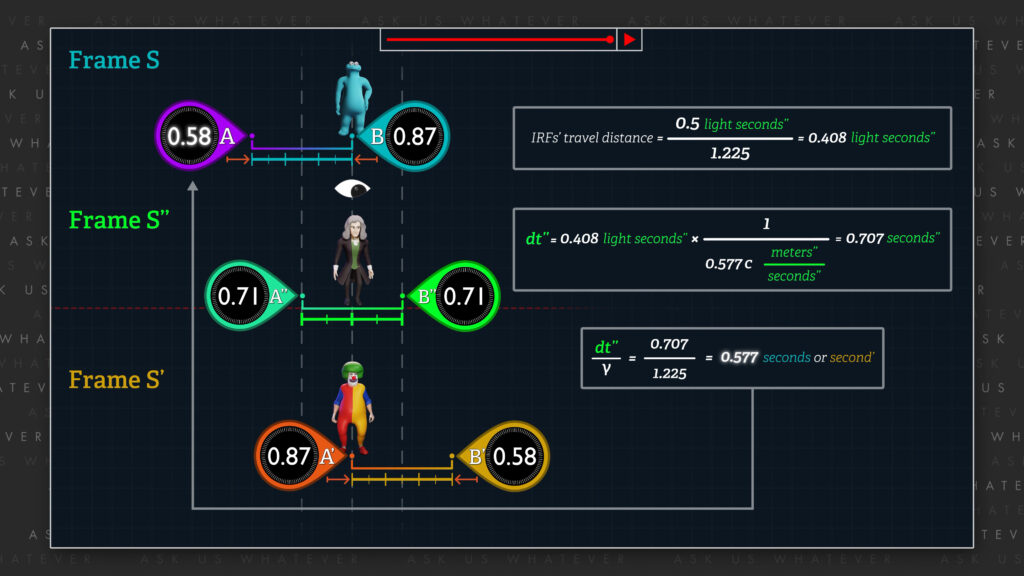
Clocks B and A’ will become aligned with our frame S’’ observer when their frames each move in opposite directions, requiring a movement of only half the distance separating clocks A or A’ from B or B’ respectively; and so, the distance that frames S and S’ must each now move is, about 0.408 light seconds’’ as viewed from frame S’’.
distance frames each must move \(= \frac{0.5\ light\ seconds^{\prime\prime}}{1.225}=0.408\ light\ seconds^{\prime\prime} \)
So, the amount of time required for frames S and S’ to now move so that Clock B becomes aligned with Clock A’ will be equal to the distance the clocks must move, 0.408 light-second’’ divided by the speed of frames S and S’ each relative to frame S’’, 0.577 times c, as measured by our neutral observer.
\(dt^{\prime\prime}=0.408\ light\ seconds^{\prime\prime}\ast\frac{1}{0.577c\frac{meters^{\prime\prime}}{second^{\prime\prime}}}=0.707\ seconds^{\prime\prime} \)
The clocks in frames S and S’ will beat at identical, time-dilated rates, 1.225 times slower than the clocks in frame S’’. And so, 0.707 seconds’’ will be equivalent to 0.577 seconds or seconds’.
\(\frac{dt^{\prime\prime}}{\gamma}=\frac{0.707}{1.225}=0.577\ seconds\ or\ second^{\prime} \)
Those 0.577 seconds turn out to have the same numerical value as the 0.577 seconds that was elapsed in what was considered the stationary frame in Episode 7.4.
That’s an interesting observation, so let’s consider what it means.
In Episode 7.4 the stationary frame S observer experienced 0.577 local seconds to have elapsed while Clock A’ in Episode 7.4 moved from its starting point, aligned with Clock A, to its ending point, aligned with Clock B.
In the current setup, the clocks in frames S and S’ advance by 0.577 local seconds and seconds’, respectively, but the observers must read from only one clock to notice this.
This re-alignment involves the movement of both frames S and S’ half the distance (from the perspective of frame S’’), but the result is that the observers will record the same number of local seconds to have elapsed as in the stationary frame in Episode 7.4, but only if they read from a single clock in their respective frames.
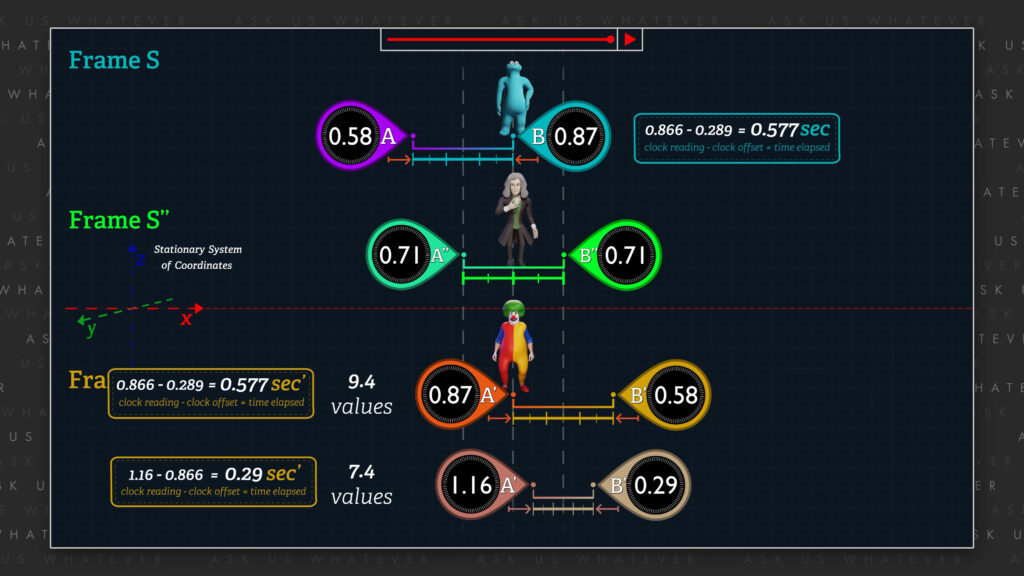
In contrast to the present result, if these observers had remained beside a single clock in their respective frames in Episode 7.4, the Master would have observed 0.577 seconds elapse in frame S, but the clown would have observed only 0.29 seconds’ to have elapsed in frame S’. So, by simply associating the stationary system of coordinates with frame S’’ in the present setup, special relativity demands that observers in frame S’ will observe a different amount of time elapsed.
So, we can put a checkmark in the favorable column for the Lorentz transformations for frame S, but a red X for frame S’. We are beginning to reveal the inconsistencies of special relativity.
Now, let’s look at clock offset.
The clocks in frames S and S’ will be offset by 0.289 seconds or seconds’ in the current setup.
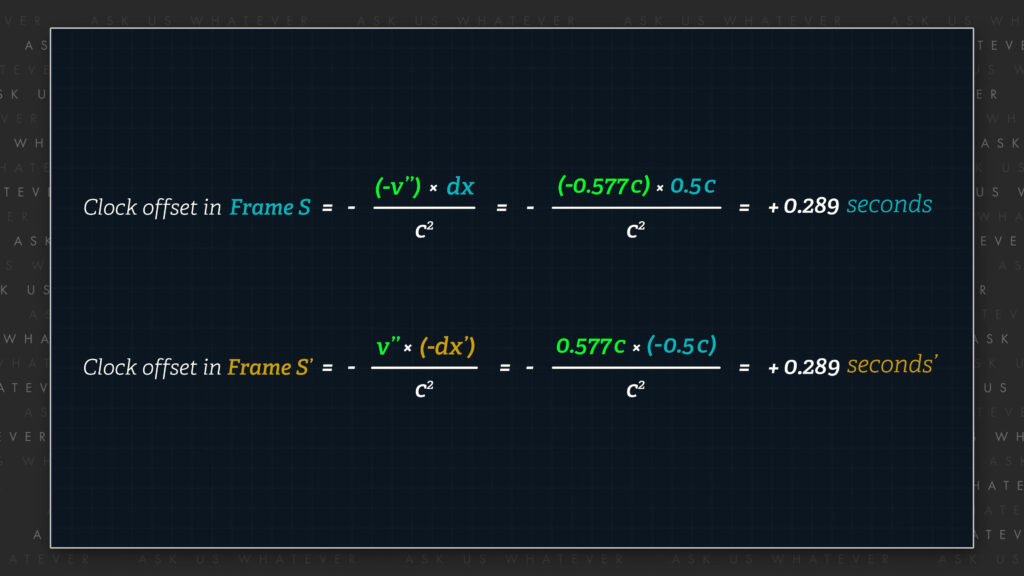
So, an observer in frame S moving from Clock A to Clock B (a point halfway between Clocks B’’ and A’’ in the present setup), will record an additional 0.289 more seconds to have elapse, whereas an observer in frame S in the Episode 7.4 moving from Clock A to Clock B experienced no clock offset at all; and an observer in frame S’ of the present setup will also experience a clock offset of 0.289 seconds’ between clocks B’ and A’, whereas an observer in frame S’ of the setup in Episode 7.4 experienced a clock offset of 0.866 seconds’ between the clocks.
This is a problem for the Lorentz transformations, because they require the physical status of real-world objects (in this case clocks) to change depending on the observer. So that’s a red X in the frame S and S’ columns.
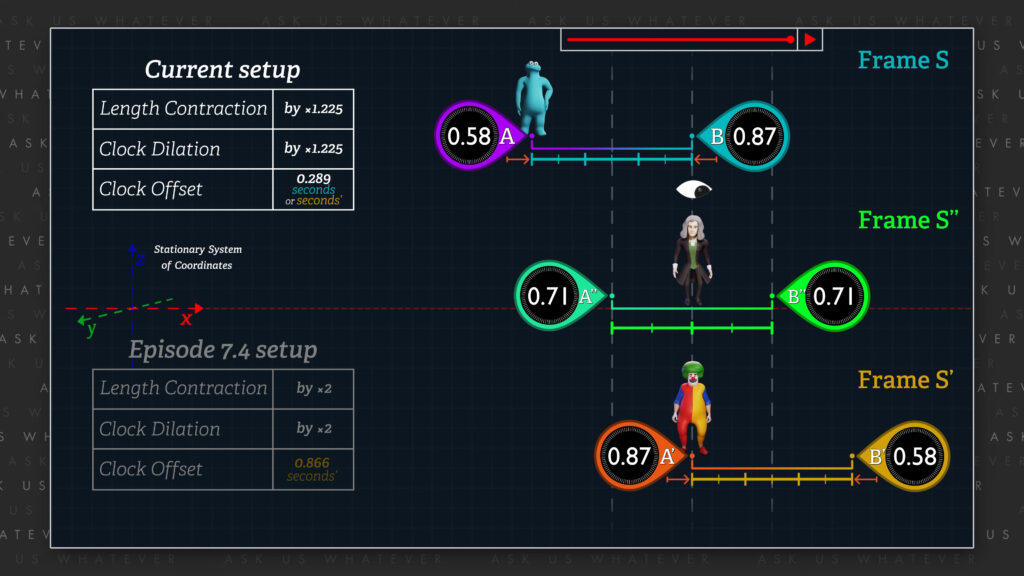
Next, let’s look at length contraction.
In Episode 7.4, the stationary observer was in frame S, and the distance between clocks in the moving frame contracted by a factor of 2, clock tempo slowed by a factor of 2, and clock offsets were 0.866 seconds’ per light second’. In the present setup, distances contract by a factor of 1.225, tempos slow by a factor of 1.225, and clocks are offset by 0.289 seconds (or seconds’) per light second (or light second’). Objects in the real world are behaving differently based merely on observer perspective. More red X’s for frames S and S’.
Lastly, let’s look at time dilation.
In Episode 7.4 the clocks in the moving frame S’ ticked at one half the rate as the clocks in the stationary frame S. In the present setup, the clocks in those same frames tick at the same rate! That’s right, since time dilation is direction-independent, the clocks in frames S’ and S both tick at identical rates, no matter how you want to work out the numerical values. Our symmetrical setup predicts no relative time dilation between clocks that displayed significant relative time dilation in Episode 7.4 when they were perceived to be moving similarly. In other words, by merely analyzing the setup from the perspective of a neutral observer in frame S’’, special relativity requires the physical properties of the clocks in frames S and S’ to magically change.
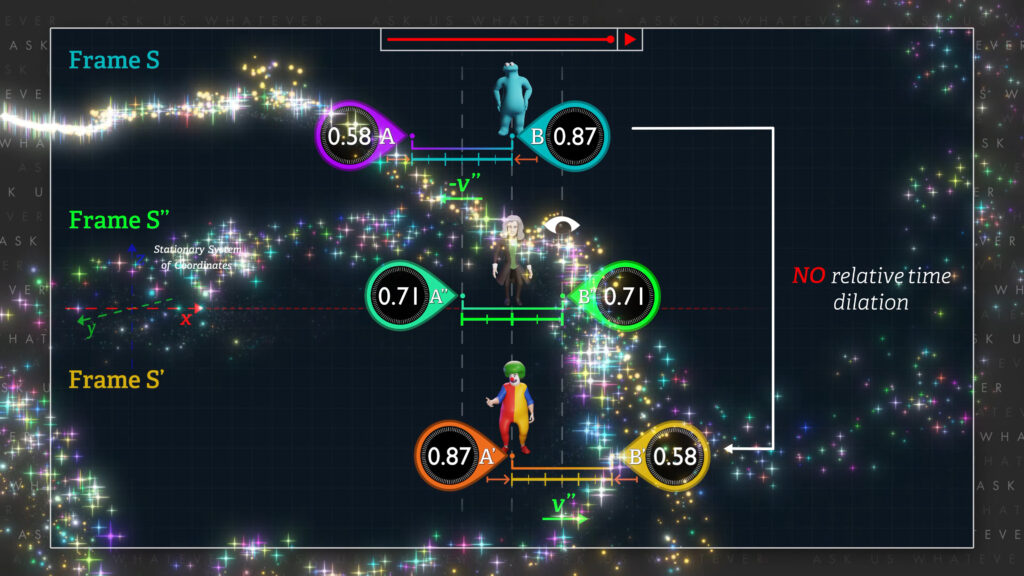
This has huge significance! Time dilation is supposed to be real! A real measurable phenomenon. The Hafele-Keating experiment, in which atomic clocks were flown around the earth in opposite directions, was supposed to be indicative of time dilation. The experiments by Chou, et al. in Science in 2010, using precision light clocks showed the effect of time dilation even at very slow speeds, and our GPS satellites also prove it every day. Yet, special relativity and the Lorentz transformations require time dilation to be an ephemeral concept that comes and goes depending on the observer’s perspective.
Our setup in Episode 7.4 was the same as it is here. We have a reference frame (here called frame S’) moving with respect to frame S at the same relative speed in both Episodes. When an observer in frame S observed frame S’ moving at 0.866 c meters per second in Episode 7.4, clocks in the moving frame ticked at half the rate as clocks in frame S.
But when we introduce frame S’’ into the picture in this Episode, such that a frame S observer seems to observe frame S’’ to move at half the speed of frame S’ in the positive x-direction, and we analyze relative distances and times from the perspective of frame S’’, all time dilation between frames S and S’ disappears, even though frames S and S’ are behaving exactly as they did in Episode 7.4.
This is absurd. Time dilation between frames S and S’ cannot disappear simply because we’ve added information by including a third frame in the analysis. Instead, we’ve exposed the soft underbelly (or perhaps the soft cerebral cortex) of special relativity. special relativity is inconsistent when expanded to 3 frames, and its inconsistency begs for a different model which involves a universal, preferred frame of reference.
So, another very big red X in the frame S and S’ columns.

Therefore, in summary, the present setup with a neutral observer allows for some additional symmetry, but it does not yield the original numerical relationships between frames, or between the objects within frames. The use of an intermediary frame and velocity addition dispenses with the need for clock recalibration, but frame S observers no longer see gamma-fold less time elapse in frame S’, and observers in frame S’ no longer see gamma-fold less time elapsed in frame S.
So even if Einstein and Lorentz had proposed an intermediary frame in an attempt to preserve symmetrical relativity between frames, they would have had to propose different amounts of length contraction, time dilation, and clock offset, based on velocity addition speeds that would not have been consistent with experimental measurements of time dilation made many years later. Thus, a model with a neutral intermediary, with all its beautiful symmetry, leads to a failed theory.
No matter what we try, special relativity fails. It is naïve and wrong to assume that we can invert the speeds of frames moving relative to each other without changing the times reported using the measuring tools in each frame. And while we can achieve symmetry between frames S and S’ through an intermediary frame S’’, such symmetry requires the use of the wrong relative speed v with respect to the other frame.
The Lorentz transformations are virtual concepts, as is special relativity. They may appear to work at low speeds, or when clock offset is ignored, or when particles are accelerated by a field operating at speed c in a local environment. But they do not reveal the mysteries of the universe.
In order to bring relativity back to a real universe, we must use transformations that rely on a speed v relative to a universal, preferred frame of reference.
Alright, that’s it for now. If you have any questions, please write them in the comments section. I’m Joe Sorge, and thanks for watching.