Welcome to Ask Us Whatever. I’m your host, Joe Sorge.
In the prior episode we showed that events may appear to be simultaneous to one observer, but not to another. Observers within the same moving reference frame may need to adjust their clocks to agree on when events occur.
In this episode, we explore something different, one of the fundamental concepts of special relativity, called “time dilation”. That is, clocks ticking at different rates. Time dilation is very counter-intuitive because in our everyday world, clocks are built to all beat at the same rate. Nevertheless, when certain types of clocks travel at very high speed, the beat rate slows down, as we’ll explain in this episode.
Einstein liked to use trains and train stations as models for some of his thought experiments. He envisioned observers in a train station, and observers on a moving train. He pointed out, as we illustrated in Episode 2, that they will experience the world differently.

He used a theoretical “light clock” that bounces a light beam vertically between two mirrors facing each other on the train. To the observers on the train, the light bounces vertically while the train travels horizontally.
Perhaps we can determine how long it takes for light to travel from one mirror to the other mirror. In a car, a good way to determine how long it will take to drive from one city to another is to take the distance between starting point and destination, and divide that distance by the speed of your car. Distance divided by speed gives us time.
We will call the time required for light to bounce from one mirror to the other \(t’ \). We use primes to keep track of things that are observed from the perspective on the train, as opposed to things that are observed from the perspective off the train. If we had measured time while we were off the train, we would have used the symbol t instead of the symbol \(t’ \). In order to compute \(t’ \) we need to know the distance between the mirrors and we need to know the speed that light travels between the mirrors. Then we will be able to determine the time it takes for light to travel from one mirror to the other.
\(t_{(0)}\ seconds’\ =\ \frac{h’ \text{meters}}{c_{y}’ \text{meters/second }^{\prime}} \)
We will call the distance between mirrors \(h’ \) meters: \(h \) is for height. And we will divide this distance by light speed, just like we divided the distance our car traveled by car speed. Now we have to be super precise when we talk about light speed here, because we are interested in vertical light speed, which you’ll see becomes important later in the episode. We’ll label the vertical direction: the y-direction. And we’ll label the horizontal direction, which is the direction the train moves, the x-direction. So, we will call the speed of light in the vertical direction on the train \(c_y’ \). The sub-y means in the vertical, or y-direction, and the prime ( \(^{\prime}\)) means as measured on the train. We call the unit of time that is used to measure time on the train \(seconds’ \) to remind us that they represent time measured with a clock on the train as opposed to time measured with a clock off the train. So, the time it takes light to travel from one mirror to the other mirror, as measured on the train, is \(h’ \) meters divided by \(c_y’ \) meters per second\(^{\prime}\). It’s a mouthful, but its accurate.
When the train is waiting in the station, the people on the platform will see the light clock inside the train bouncing at the same rate as people on the train.
\(t_{(0)}\ \text{seconds}\ =\ \frac{h\ \text{meters}}{c_{y}\ \text{meters/second}} \)
When the train has zero speed, the time for light to bounce from mirror to mirror, as measured by people in the station, which we will call \(t \) seconds (note that we are not using the prime symbol for t or the prime symbol for seconds since these are being measured from off the train), is the distance traveled, \(h \) meters, divided by the vertical speed of light, \(c_y \) meters per second. Note that we are using \(h \) and \(c_y \), not \(h’ \) and \(c_y’ \) since the distance traveled, \(h \), and the light speed, \(c_y \), are being measured from off the train.
In special relativity, distances that are at right angles to the direction of motion, such as \(h’ \) and \(h \), are not affected by train speed. \(h \) will simply equal \(h’ \) whether the train is moving or not.
Now Einstein believed that light can only travel at a fixed speed, about 300 million meters per second. No faster and no slower. When the train is not moving, the light rays that strike the upper mirror and then bounce back to the lower mirror travel in the vertical direction. These are the rays that persist in the imaginary light clock when the train is not moving. So, the speed of the vertically-moving light rays, which we call \(c_y \) if we are observing from the platform and we call \(c_y’ \) if we are observing from inside the train car, both will equal the total speed of light, \(c \), about 300 million meters per second or second\(^{\prime} \) depending on our vantage point. And since \(h \) and \(h’ \) are the same, \(t \) will equal \(h \) divided by \(c \), which will equal \(t’ \) which will equal \(h’ \) divided by \(c \). Both vertical heights are the same, and both speeds of light are the same when the train is still.
\(t_{(0)}\ =\ \frac{h}{c}\ =\ t_{(0)}’\ =\ \frac{h’}{c} \)
But when the train starts moving, things change. People in the station will see a train whizzing by; and as they peer into the windows of the train, they’ll see the light bouncing on a bit of a diagonal.

As the light travels from the mirror on the floor to the mirror on the ceiling of the train, the train moves forward a bit. Some of the light rays that were emitted from the bottom mirror at a slight, forward angle reach the top mirror as the train advances. The light then bounces at an angle back toward the mirror on the floor. Provided the angles and speeds stay the same, the light will continue to bounce from mirror to mirror.
So now, the relevant light rays are those that travel diagonally at a slight forward angle. The vertical light rays are no longer able to remain inside the clock. They get left behind as the train advances.
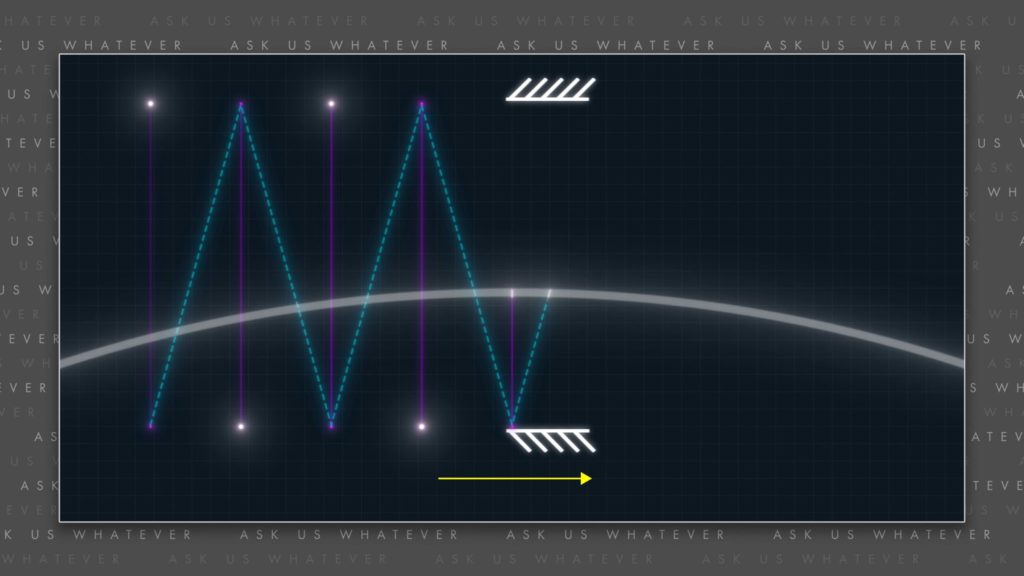
Light doesn’t care about the air inside the train car, and does not acquire momentum. Light only cares about where it is in space. And as the train travels through space, light continues to move in its original direction through space, oblivious as to the movement of the train. So, in order for the light rays to continue to bounce between the mirrors of the light clock, they must be oriented at a slight, forward angle.
Let’s consider a fireworks display as an example. If a rocket is shot skyward at an angle, observers sitting perpendicular to its path will see the rocket moving diagonally. But for observers facing parallel to the motion of the rocket, it will appear to be heading straight up.

The observers who only see it moving upward will see only the vertical component of the rocket’s velocity, and will think that this is the total speed of the rocket. But observers who are sitting perpendicular to its path will know that the vertical speed is only one component of the rocket’s speed, the y-component, which is analogous to the y-component of light speed, \(c_y \), as seen by people in the station.
\(\text{vertical component of} \)
\(\text{light speed}\ =\ c_y \)
The people sitting parallel to the rocket cannot see the horizontal component of speed that makes up part of the rocket’s total diagonal speed. Just like the people sitting in the train car cannot see the horizontal component of light speed in the forward-moving light clock.
horizontal component of light speed \(=\ c_x \)
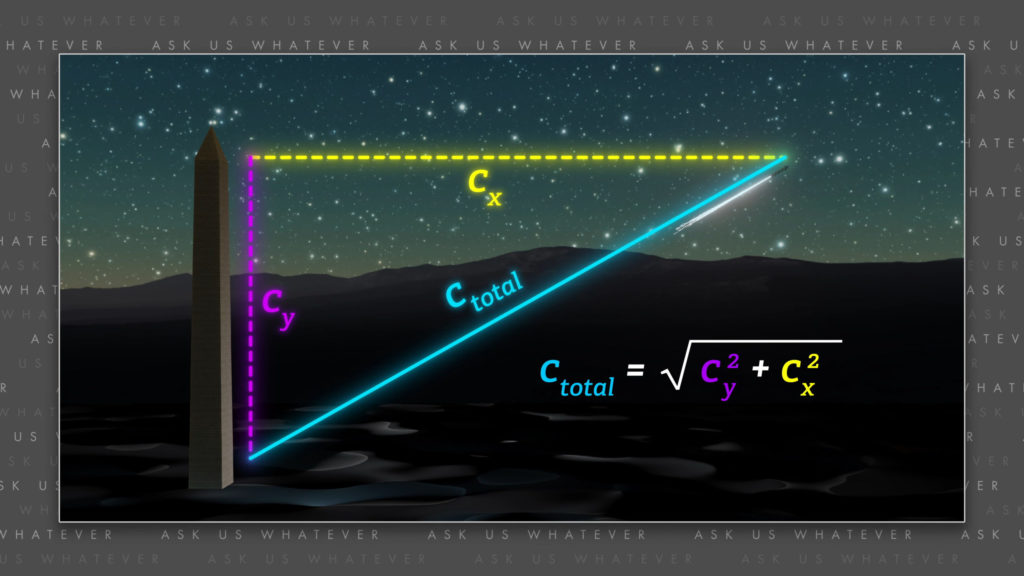
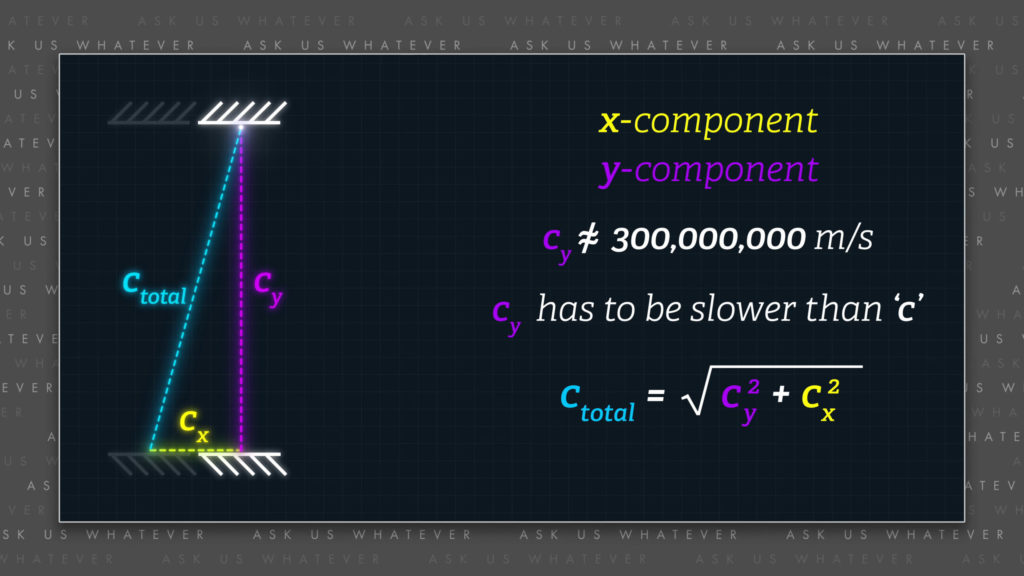
We can call the horizontal component of rocket speed, or light speed, \(c_x \). The total speed of the rocket (or light) is the Pythagorean sum of the vertical and horizontal speeds.
\(c_{total}\ =\ \sqrt{c_{y}^{2}\ +\ c_{x}^{2}} \)
The total speed \(c \) equals the square root of \(c_y \) squared plus \(c_x \) squared.
According to our every-day experience, adding a second dimension of speed to something that is already moving in one direction, would simply increase its total speed. If you bounce a ball on a train, the ball bounces at the same speed vertically whether the train is moving or not. When the train moves horizontally, someone in the station will see your ball bouncing diagonally, with both vertical and horizontal components to its new, greater diagonal speed. For a ball, the train’s motion simply adds more overall speed to the ball. It moves faster diagonally that its original vertical speed when the train was in the station.
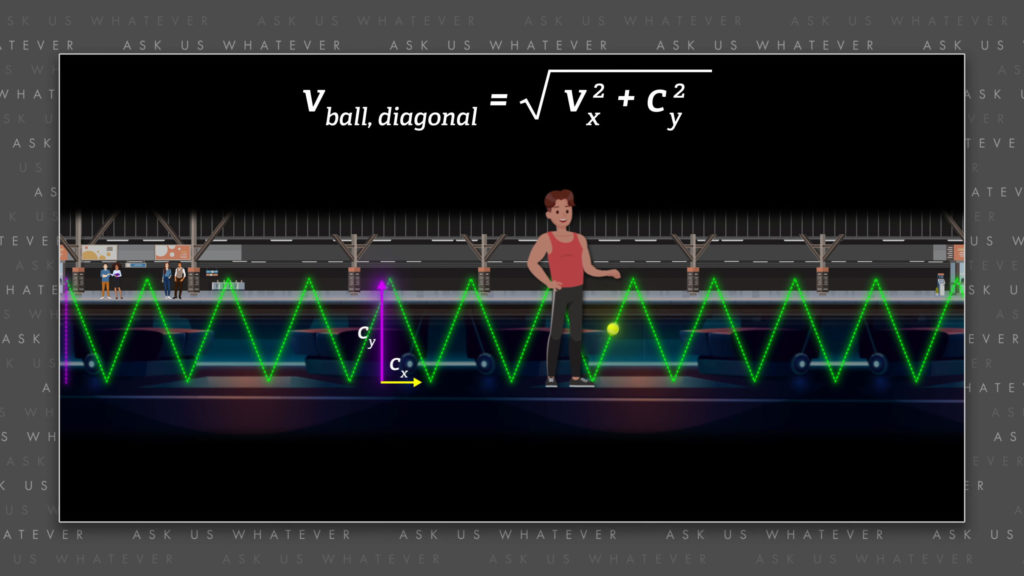
But according to Einstein, light is different. It cannot move faster or slower than about 300 million meters per second through space, regardless of its direction and regardless of the motion of its source. So, \(c_{total} \) cannot get larger, or smaller than about 300 million meters per second. And if so, a once-vertical light beam is tilted at a slight forward angle, it acquires an x-component to its speed, \(c_x \); which means that the y-component to its speed, \(c_y \), can no longer be 300 million meters per second. The y-component has to be slower so that the x and y components, when plugged into the Pythagorean formula, add up to the total, diagonal speed of light. Simply put, the light now travels about 300 million meters per second diagonally, and less than about 300 million meters per second in the x-direction and less than about 300 million meters per second in the y-direction. Keep in mind that this will be true for all forms of electromagnetic radiation, including radio waves, x-rays, etc.
The analogy here is that people in the station are like the people who can see the diagonal motion of the rocket, and thus can appreciate both the x- and y-components of light speed. But people on the train are oblivious to the x-component of light speed. They only see the vertical, y-component. In a way, they are being deceived by their surroundings.
Now, to quantify this, from the perspective of the observers in the station, the light not only travels the distance from floor to ceiling, it also travels the distance that the train moves. We can think of these distances as the sides of a right triangle.
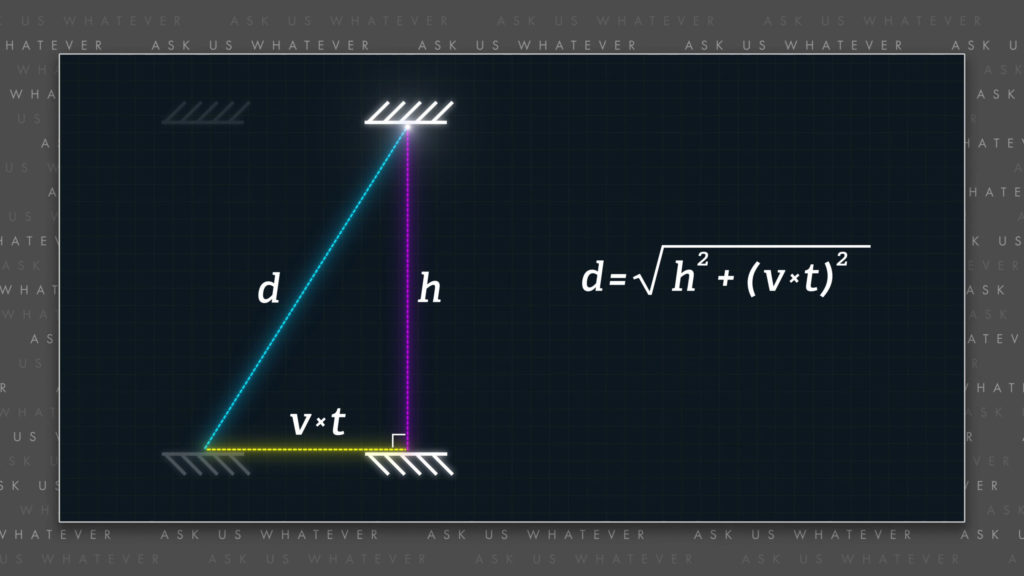
The vertical side of the triangle would have length \(h \), or \(h’ \) if we measure it on the train, the distance from floor to ceiling. The horizontal side of the triangle represents the distance the train moves while the light travels from mirror to mirror. This will equal the speed of the train, \(v \), multiplied by the light’s travel time from floor to ceiling, \(t \).
The diagonal distance that light travels from floor to ceiling we’ll call \(d \). We can find it using the Pythagorean theorem. The diagonal side of a right triangle is the square root of the sum of the squares of the other two sides.
\(d\ =\ \sqrt{h^{2}\ +\ (vt)^{2}} \)
\(d \) equals the square root of the height squared plus the horizontal distance the train moves, squared. And, as we know, the diagonal distance, \(d \), will be longer than the vertical distance, \(h \).
Now, since Einstein believed that light travels at a constant speed through space, it should take a longer amount of “time”, in other words a longer duration, for it to complete a diagonal journey, since the distance is longer than the vertical distance \(h \). The time required for light to travel the diagonal distance, as seen from the stationary frame will be,
\(t\ =\ \frac{d}{c} \)
the diagonal distance divided by total light speed. Note that we are no longer using \(h \) in the numerator. We’ve replaced it with \(d \), since the people in the station observe a diagonal light path. And we are no longer using \(c_y \) since the people in the station observe light traveling at an angle at its full speed, not just up and down.
Let’s compute the time required for light to travel the longer, diagonal distance. We will simply substitute our Pythagorean formula for \(d \), into the numerator, and this will make time, as seen from the stationary frame, dependent on train speed \(v \).
\(t_{(v)}\ =\ \frac{\sqrt{h^{2}\ +\ (vt)^{2}}}{c} \)
The time required for light to travel the diagonal distance, as seen by people in the station is the square root of \(h \)-squared plus \(v \)-times-\(t \)-squared all divided by \(c \). Notice that if the train stops moving, its speed \(v \) goes to zero and the equation for time resolves back to the original.
\(t_{(0)}\ =\ \frac{\sqrt{h^{2}\ +\ 0}}{c}\ =\ \frac{h}{c} \)
\(t_{(0)} \) equals \(h \) divided by \(c \). But when the train is moving, we can see that the time, as measured in stationary seconds, increases because the numerator increases.
So, let’s solve for \(t \) when the train is moving. This takes a few algebraic steps that you can examine by stopping the video here,
\(t =\ \frac{\sqrt{h^{2}\ +\ (vt)^{2}}}{c} \)
\(t^{2}\ =\ \frac{(h^{2}\ +\ v^{2}t^{2})}{c^{2}} \)
\(c^{2}t^{2}\ =\ h^{2}\ +\ v^{2}t^{2} \)
\(c^{2}t^{2}\ -\ v^{2}t^{2}\ =\ h^{2} \)
\(t^2 (c^{2}\ -\ v^{2})\ =\ h^{2} \)
\(t^{2}\ =\ \frac{h^{2}}{c^{2}\ -\ v^{2}} \)
\(t^{2}\ =\ \frac{h^{2}}{c^{2}}\ \times \ \frac{1}{1\ -\ \frac{v^{2}}{c^{2}}} \)
\(t\ =\ \frac{h}{c}\ \times\ \frac{1}{\sqrt{1\ -\ \frac{v^{2}}{c^{2}}}} \)
We find that the time for light to travel the diagonal distance is the original vertical distance \(h \) divided by \(c \) times a complicated factor: 1 divided by the square root of 1 minus \(v \)-squared over \(c \)-squared. This complicated factor is the Lorentz factor that we mentioned in episode 2.
\(\text{Lorentz Factor } =\ \frac{1}{\sqrt{1\ -\ \frac{v^{2}}{c^{2}}}} \)
The Lorentz factor is usually referred to with the Greek letter gamma,
\(\gamma =\ \frac{1}{\sqrt{1\ -\ \frac{v^{2}}{c^{2}}}} \)
It’s a very important factor in special relativity, and it’s well worth memorizing this formula.
So, when the train is parked in the station, \(v \) equals zero, and the Lorentz factor simply equals one.
\(\gamma\ =\ \frac{1}{\sqrt{1\ -\ \frac{0^{2}}{c^{2}}}}\ =\ \frac{1}{\sqrt{1-0}}\ =\ 1 \)
In this case the time for light to bounce vertically from mirror to mirror will be
\(t_{(0)}\ =\ \frac{h}{c}\ \times\ 1\ =\ \frac{h}{c} \)
\(h \) divided by \(c \) times 1, which is simply the original h divided by \(c \). But when the train moves, its speed \(v \) grows and the Lorentz factor increases. The Lorentz factor, gamma, will always be a positive number, and never smaller than 1. And so, the time required for light to bounce from mirror to mirror grows as the train moves, in proportion to the Lorentz factor.
This is called time dilation. Einstein believed that the slowing of the train’s light clock will only be perceived by the people in the station, since the people on the train don’t know that they are observing only a slower, y-component of light speed, just like the people who could only see the fireworks display moving vertically. Einstein also believed that people on the train will be oblivious to the longer distance traveled along the diagonal. They will only see light bounce vertically.
Since
\(c_{total}\ =\ \sqrt{c_{y}^{2}\ +\ c_{x}^{2}} \)
total light speed, as denominated in seconds, equals the square root of the y-component of light speed squared plus the x-component of light speed squared, you can see by pausing the video to examine the fast algebra, that
\(c_{total}\ =\ \sqrt{c{y}^{2}\ +\ c_{x}^{2}} \)
\(c_{total}\ =\ \sqrt{c_{y}^{2}\ +\ v^{2}} \)
\(c_{total}^{2}\ =\ c{y}^{2}\ +\ v^{2} \)
\(c_{total}^{2}\ -\ v^{2}\ =\ c{y}^{2}\ \)
\(c_{y}\ =\ \sqrt{c^{2}_{total}\ -\ v^{2}}\ =\ \sqrt{c^{2}\ -\ v^{2}} \)
\(c_{y}\ =\ c\ \sqrt{1-\ \frac{v^{2}}{c^{2}}}\ =\ \frac{c}{\gamma}\ seconds \)
the y-component of light speed is simply total light speed divided by gamma. Which confirms that the period \(t \) of the train clock, as seen by people in the station, will be longer by a factor of gamma than a clock in the station. And this is because the ticker of the light clock on the train slows down when the train moves. The ticker on the train is the vertical component of light speed, \(c_y \), and since \(c_y \) decreases when the speed of the train, \(v \), increases, the ticker of the light clock on the train ticks more slowly.
To simply this, the number of stationary seconds is equal to the number of moving seconds \(^{\prime}\) multiplied by gamma,
\(t\ =\ \gamma t^\prime \)
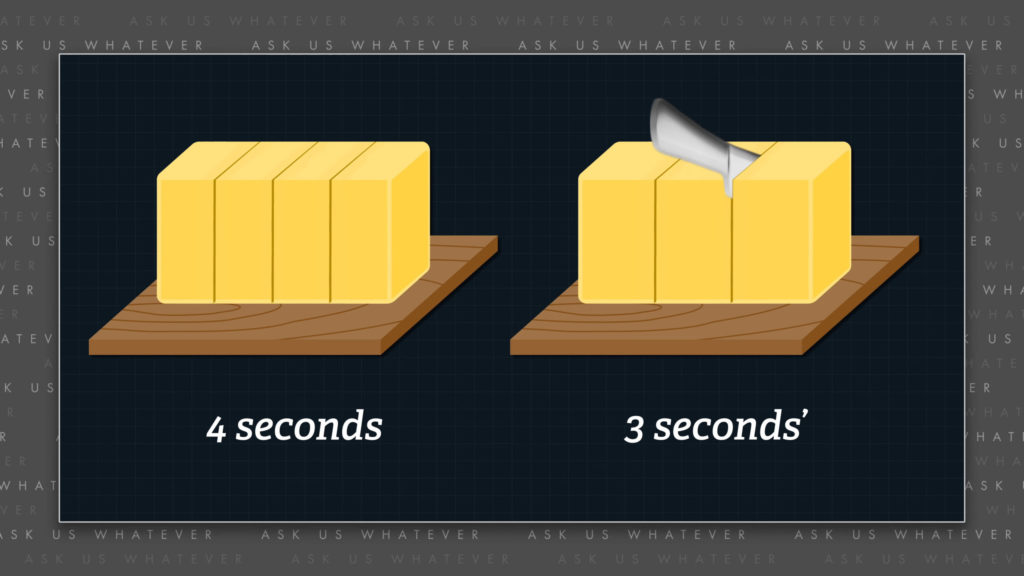
To drive this home, picture two identical sticks of butter.

If we divide one stick into 4 equal-sized pieces, which we will call seconds, and the other stick into 3 equal-sized pieces, which we will call seconds\(^\prime \), then
\(4\ \frac{seconds}{stick}\ =\ 3\ \frac{seconds^\prime}{stick}\)
four seconds per stick equals 3 seconds\(^\prime \) per stick. The sticks represent events of the same duration. The durations of the events are simply divided into a different number of segments based on the tick-rate of the clock being used to slice up the durations.
The gamma factor is the conversion factor for the two different types of pieces. In this example, gamma would be 4 divided by 3. If we multiply
\(3\ seconds^\prime\ \times\ \frac{4}{3}\ \frac{seconds}{seconds^\prime}\ =\ \)
\(4\ seconds \)
3 seconds\(^\prime \) by 4 divided by 3 seconds per \(\text{seconds}^\prime \) we get 4 seconds.
\(t\ seconds\ =\ \)
\(t^\prime\ seconds\ \times\ \gamma\ \frac{seconds}{seconds^\prime}\)
In more general form, \(t^\prime \) seconds\(^\prime \) times gamma seconds per seconds\(^\prime \) is equal to t seconds.
All right, what’s the bigger message here? It’s not about the algebra. It’s about time. Time is like the sticks of butter, and clocks are like the knife. Certain types of clocks slow down when moving relative to another reference frame. But “time” does not change. The term “time-dilation” is misleading, because “time”, a concept that we’ll get into more deeply in later episodes, does not dilate or slow down or stretch or anything of the kind on a universal scale. Time is about distance and speed, and the tempo of our clocks does not change distances or speeds in other frames of reference, only our perception of them. Nevertheless, we can change the tempo of events within our frame of reference by moving very fast, and this may impact the rate at which we age relative to other frames of reference.
OK that’s the end of Time Dilation Part 1. The next video will expand upon some of the implications of time dilation, some of which are relevant to our everyday lives.
If you have any questions, please write them in the comments section. I’m Joe Sorge and thanks for watching.