Welcome to Ask Us Whatever. I’m Joe Sorge.
Well, the comments I received in response to Episode 7.1 showed me that many people do not understand Einstein clock synchronization, nor its profound implications. And because Einstein clock synchronization is essential to understanding special relativity, we need to shore up our understanding of this very unusual way to adjust clocks.
Alright, let’s start with a quote from Einstein’s 1905 paper on Special Relativity:
If at the point A of space there is a clock, an observer at A can determine the time values of events in the immediate proximity of A by finding the positions of the hands which are simultaneous with these events. If there is at the point B of space another clock in all respects resembling the one at A, it is possible for an observer at B to determine the time values of events in the immediate neighborhood of B. But it is not possible without further assumption to compare, in respect of time, an event at A with an event at B. We have so far defined only an “A time” and a “B time”. We have not defined a common “time” for A and B, for the latter cannot be defined at all unless we establish by definition that the “time” required by light to travel from A to B equals the “time” it requires to travel from B to A.
The word “time” is in quotes because in this paragraph, Einstein changes the standard definition of the word time. He is basically saying that we are going to adopt a convention whereby we re-map time, so that two events that take place within a given reference frame, which may or may not be of different durations, are, by definition, going to be deemed to be of the same duration.
This is like saying that if we place a pea on a balance scale, and then we do the same with an apple, and we would like a pea to weigh the same as an apple, well, we can simply calibrate the scales to make it appear that the pea weighs the same as the apple.

If you don’t think that’s what he states in the 1905 relativity paper, let’s read further:
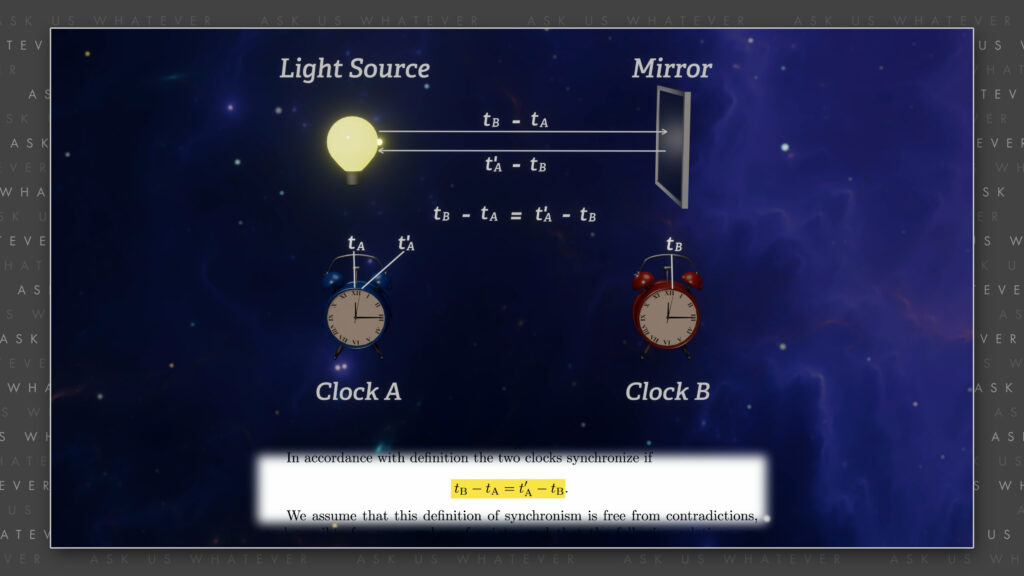
Let a ray of light start at the “A time” \(t_A \) from A towards B, let it at the “B time” \(t_B \) be reflected at B in the direction of A, and arrive again at A at the “A time” \(t^{\prime}_A \). In accordance with definition the two clocks synchronize if…
\(t_{B}\ – t_{A} = t^{\prime}_A – t_B \)
…The reading from clock B at the instant light strikes the mirror at B minus the initial reading from clock A when light first left point A, in other words, the way we will now quantify the duration of the trip from clock A to clock B in that reference frame, must equal the final reading from clock A when the light returned to A minus the reading from clock B at the instant light struck the mirror at B, in other words the way we will now quantify the duration of the trip from clock B back to clock A in that reference frame. So, he is saying that we will deem, like royalty from the throne, both one-way trips to take the same amount of “time” whether they really do or not.
You might be wondering, “what’s the big deal?” According to Einstein, light travels at the same speed in all reference frames, so the time it takes for light to travel from clocks A to B will always equal the time it takes to return from clock B to A, right? But that’s backwards, and not at all what Einstein was getting at. Light speed is perceived to be constant in both directions in the moving frame because of his method for synchronizing clocks, not because Einstein or other scientists have demonstrated the one-way speed of light to be constant.
There’s a whole literature of peer-reviewed articles that go into this in gory detail. And there’s an excellent Veritasium video on the subject called “Why No One Has Measured The Speed Of Light”. We’ll put some references and links up on the Ask us Whatever web site so you can follow up if you’re interested. But basically, there are two camps in the debate about light speed and clock synchronization: Those who claim that Einstein created a rigged “convention” for clock synchronization, they are called the conventionalists.
The conventionalists claim that light could possibly travel at different speeds in different directions, and only the round-trip speed of light is constant.
And then there are the anticonventionalists, who claim that Einstein had good reasons, beyond mere convention, for choosing his clock synchronization protocol. The anticonventionalists argue that the conventionalist synchronization methods potentially violate Newton’s laws of motion, even at relatively slow speeds, and the debate still continues in the scientific literature through today. So, let’s try to develop some insight to help us choose a side.
We’ve all seen movies where a gang of criminals huddle together to make sure their wristwatches report exactly the same time, so that when they carry out the steps of an intricate robbery, their actions occur in precise sequence. We typically say that they synchronized their clocks at the start.

But that procedure is not what Einstein meant when he defined synchronized clocks. In fact, it’s almost the opposite, since Einstein-synchronized clocks can, and do, report different times of day, not the same time of day. Unfortunately, the relativity literature calls Einstein synchronization “standard” synchronization, even though it is far from what most people would call standard. It really should be called clock coordination, not clock synchronization.
And if you look at Einstein’s 1905 relativity paper, you’ll see that he plainly states in Sections 2 and 3, that an observer in a frame of reference that is moving relative to another reference frame in which there are two Einstein-synchronized clocks A and B, will not see clocks A and B as being synchronized. He proposed a thought experiment in which a rigid rod and an observer are in a reference frame that is moving with respect to the reference frame of clocks A and B.
Here’s a quote:
Observers moving with the moving rod would thus find that the two clocks were not synchronous, while observers in the stationary system (meaning the clock frame) would declare the clocks to be synchronous.

To start out, please note that clocks A and B are in the same inertial reference frame. So, they beat at the same tempo. Time dilation does not cause the readings on these clocks to drift away from each other, provided the clocks remain at the same locations within their moving reference frame.

Let’s hand the rod to our master of the universe from Episode 3, and place the rod and the master in a frame in which they see the clock frame moving in the positive x-direction.

Let’s have some fun and bring Einstein back to life and position him next to clock A.

He and the clock are being carried along in the moving frame in the positive x-direction. And let’s say that our clown from Episode 7.1 stands next to a mirror beside clock B such that the clown, mirror, and clock B are also being carried along in the positive x-direction in the same moving frame as Einstein and clock A.

Now, Einstein aims a laser light at the mirror next to the clown, and as he flashes the light, Einstein notes the reading on clock A. We’ll call this clock reading \(t_A \).

And as we know, light travels fast, but not instantaneously. So, it takes a moment for light to travel toward the clown and mirror at clock B, during which the reference frame, including the mirror and clock B, moves a bit in the x-direction.
So from the perspective of the master of the universe, the distance that light must travel from clock A to the moving mirror at clock B will be a bit longer than the static distance between clocks A and B, as measured when the reference frame is not moving, or as measured by Einstein and the clown whether the reference frame is moving or not. Einstein calls the static distance the proper distance between A and B.

Einstein made the assumption in Section 2 of his 1905 paper that the amount of time (which we will call a duration here until we get more specific) required for light to travel from clock A to clock B from the perspective of an outside observer, such as our master of the universe, is equal to
\(duration(AB)=\frac{r_{AB}}{(c-v)} \)
\(r_{AB} \) divided by \(c \) minus \(v \), where \(r_{AB} \) is the distance between clocks A and B as perceived by the master of the universe. The duration is longer than simply \(r_{AB} \) divided by \(c \) because Clock B is moving away from the approaching light beam.
This formula, straight out of Einstein’s 1905 paper, makes a few profound statements. The first is that according to Einstein, light travels at speed \(c \) within some frame (in our example, in the master of the universe’s frame), but is moving at speed \(c \) minus \(v \) relative to another frame (in our example, relative to the clock frame).
In other words, a light ray traveling at speed \(c \) in some light ray frame, and in the same direction as the moving reference frame, will be moving at speed \(c \) minus \(v \) relative to that moving reference frame. And that the duration of time required for light to travel a distance \(r_{AB} \) through that reference frame as it moves, will take longer if the reference frame is moving at speed \(v \) in the same direction as the light ray, all as observed by someone in another reference frame, such as by the master of the universe.
Likewise, if the light travels opposite to the direction of motion of the moving reference frame, let’s say from the mirror at clock B back to clock A, Einstein states that the time required to make that return journey will be, from the perspective of the master of the universe,
\(duration(BA)=\frac{r_{AB}}{(c+v)} \)
the distance between clocks A and B, \(r_{AB} \), divided by speed \(c \) plus \(v \).
This is because clock A is now moving toward the reflected light ray, as compared to when clock B was moving away from the original light ray.
Again, Einstein makes a profound statement with this formula; that a light ray traveling opposite to the direction of a moving reference frame will travel at speed \(c \) in some frame, but will interact with the moving reference frame at speed \(c \) plus \(v \), and so the journey from the mirror at clock B back to clock A will be of a shorter duration than the journey from clock A to clock B. Did you hear that? Shorter duration. i.e., according to Einstein’s formula, right out of his 1905 paper, it takes less time for light to travel the very same distance from clock B back to clock A.
Given that Einstein’s formulas clearly reveal that these downstream and upstream durations are not equal, as measured by an observer in another frame, how can he arrange for light to appear to travel at the same speed in both directions in the frame of the clocks? Well, the trick is in what he does with the clocks!
Einstein states in Section 1 of the 1905 paper,
…it is not possible without further assumption to compare, in respect of time, an event at A with an event at B.
That is, an observer at clock A does not know what the reading on clock B will be when light strikes the mirror at clock B, nor does an observer at clock B know the reading at clock A when light either was emitted or returns to position A.
Einstein realized that he can manipulate the readings reported by clocks A and B at will, without observers at position A knowing that he manipulated Clock B or vice versa. He therefore manipulates the clocks so that they do not report the same time of day, and thereby forces the quantitative measurement of travel times to appear to be equal even though the travel times are not equal.
Like defining the weight of an apple to be the same as the weight of a pea, because that’s how you’d like things to be.

Frankly, I have to admit that this is not entirely unreasonable given the circumstances, because his underlying assumption is that light travels at a constant speed \(c \) in both directions in some other reference frame (in our example the master of the universe’s reference frame), and his process for adjusting clocks merely transforms the numerical value of light speed in the moving frame so that it equals the numerical value of light speed observed from the other frame. So, if you wish to perform physics calculations in the moving frame, Einstein’s transformation allows your formulas to use the speed of light as observed by the master of the universe rather than as observed by you in the moving frame, which says something about Einstein’s respect for the universality of the frame in which the master of the universe resides. Sorry, I’m not trying to be religious here, not at all, I’m just pointing out that Einstein’s logic has implications that are consistent with some universal preferred frame of reference in which light travels at a constant speed; and that he manipulates the clocks in other moving reference frame so that it appears that light travels at the same, constant speed in them as well. I’ll argue in a later episode that such a reference frame cannot be an arbitrary reference frame, because the Lorentz transformations are not linearly additive. And so, the laws of physics would change in every inertial reference frame if we simply compared the speeds of such frames to index frames that we arbitrarily deem to be stationary. I know that sounds a little complex, but we’re going to get to it.
Anyway, Let’s work through a numerical example to see how his synchronization method works in practice. Let’s assume that Einstein, the clown, the mirror, and clocks A and B are in a reference frame that is moving at about 87% of speed \(c \) relative to the master of the universe, in positive the x-direction.

I choose this speed since it results in a Lorentz factor equal to approximately 2, and that makes the math easier.
Suppose that Einstein flashes a laser light toward clock B when clock A strikes 12 noon.

Let’s say that the proper distance between clocks A and B is 1 light second’ (approximately 300 million meters),
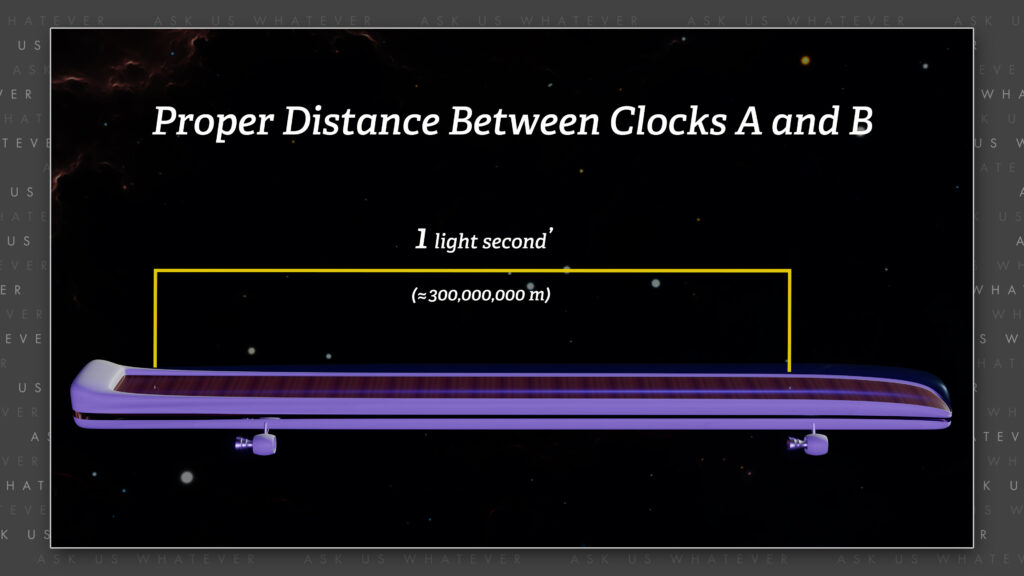
but now that Einstein’s frame is moving at about 87% of \(c \), the distance between clocks A and B has contracted to about half the length as seen by the master of the universe. (By the way, you know I don’t believe in length contraction, but if I’m going to explain Einstein clock synchronization, I have to include it.) Anyway, if we apply Einstein’s formula for the travel duration along the length-contracted distance from clock A to the mirror at clock B, as measured by the master of the universe using cosmic train station clocks, we obtain,
\(\text{downstream duration(seconds)} = \)
\(\frac{r_{AB}}{\gamma_{L}} \times \frac{1}{(c-v)} = \)
\(\frac{1}{2} \times \frac{1}{1-0.87} \simeq 3.73 \)
about 3.73 cosmic train station seconds. And since the moving frame’s clocks are ticking at half the rate of the cosmic train station clocks, due to time dilation, the downstream duration in the moving frame will be about 1.87 seconds’.
And if we apply Einstein’s formula for the return trip, we get
\(\text{upstream duration(seconds)} = \)
\(\frac{r_{AB}}{\gamma_{L}} \times \frac{1}{(c+v)} = \)
\(\frac{1}{2} \times \frac{1}{1+0.87} \simeq 0.27 \)
about 0.27 cosmic train station seconds, which would be about 0.13 seconds’ using moving frame clocks.
Now, the round-trip travel time is therefore 4 seconds when measured with a cosmic train station clock, and 2 seconds’ in the moving clock frame.
Now Einstein notes the reading on clock A when the reflected light ray returns, and it shows 12 noon plus 2 seconds’.
Which delights him, since that’s exactly how long he believes a 2 light-second’ round-trip journey should take.

Einstein, hoping that the light struck the mirror at clock B 1 second’ after 12 noon, which is what clock B would report if the clocks are already synchronized according to Einstein’s protocol, he video calls the clown on his cell phone.

EINSTEIN: “Hey dingbat, what time did clock B show when my light hit the mirror?”
CLOWN: “Nice outfit you’re wearing.”
EINSTEIN: “You’re joking no?”
CLOWN: “Do I look like the kind of guy who would joke?”
EINSTEIN: “OK enough with the riddles! What time was on the clock when the light struck the mirror.”

CLOWN: “My talents are completely under-appreciated.” The clown pauses, and then looks at his phone. “12 noon plus 1.87 seconds’ .”
EINSTEIN: “Scheisse!” Einstein throws his phone in anger.

Whoa, he’s got a temper. Recall, according to Einstein’s equation,
\(t_B \ – t_A = t^\prime_A – t_B \)
he must somehow make the difference in clock readings for the “downstream trip” from A to B equal the difference in clock readings for the “upstream trip” from B back to A. If the clocks are synchronized the way he likes it, then \(t_B \) should equal \(t_A \) plus one half the round-trip travel time. Which means that he needs to reduce the time difference calculated for the downstream trip from 1.87 seconds’ to 1 second’, and he needs to increase the time calculated for the return trip from 0.13 seconds’ to 1 second’.
Einstein calls the clown again.
EINSTEIN: “Push clock B’s time back 0.87 seconds’, and we’ll do it again.”
CLOWN: “You ask a lot from an underpaid guy in a clown suit.”
EINSTEIN: “I really don’t have time for this.”
CLOWN: “No? I thought you were the guy who’s in control of time.”
EINSTEIN (sarcastically): “Very clever.”
CLOWN: “Thought you’d never notice.”
EINSTEIN: “Enough! Let’s just get going.”
So now, after the clown has adjusted clock B to read 0.87 seconds’ earlier, and one minute has passed, we see that clock A reports 12 noon plus one minute’, and clock B reports 12 noon and 59.13 seconds’. Clocks A and B now report different times, by 0.87 seconds’.
EINSTEIN: “OK we start again at 12:02!”
GFX: Einstein flashes the laser light when clock A reads 12:02 pm, and clock B reads 12:01:59:13. The light travels for 1.87 seconds’.
The light strikes the mirror when clock B reads 12:02 pm plus 1 second’.
Einstein calls the clown.
EINSTEIN: “What did you see this time?”
CLOWN: “I saw a beautiful, pencil thin red stream of light, like…. Like when an assassin searches for you in the dark.”
EINSTEIN: “Dummkopf! No, what time did the clock show when the red light hit the mirror?”
CLOWN: “Hmm, well, let’s see…. 12:02 pm plus 1 second’.”
EINSTEIN: “Perfect! We are in sync!”
CLOWN: “Do you really think so? Because I’m not feeling the chee.”
EINSTEIN: “Acch! Go on, pick up your paycheck and get out of here.”
With the clocks now reporting different offset times of 0.87 seconds’, the recorded travel time from clock A to clock B now appears to be 1 second’ (1.87 seconds’ minus the 0.87 seconds’ that Einstein had the clown offset clock B). And the travel time of the reflected light now also appears to be 1 second’ (0.13 seconds’ plus the 0.87 seconds’ that Einstein had the clown offset clock B). A single adjustment of clock B, without any change to clock A, created an apparent equalization of travel times!
And so such an offset can cause observers in the moving frame to believe that light is traveling for the same amount of time over equal forward and return distances (from their perspective), and therefore they’ve been led to believe that light is traveling at the same speed in both directions. But it’s not. Even Einstein says that it’s not in his paper!
Still don’t believe me? Well, we’ll include some peer-reviewed references on the Ask us Whatever web site, including Einstein’s paper, and including papers on the global positioning system. So let’s look at the language Einstein used to qualify postulate 2 in his 1905 paper.
…where time interval is to be taken in the sense of the definition in Section 1.
And Section 1 is the section that describes his synchronization convention. Einstein’s constant speed of light postulate, you know, his second postulate, the one that everyone thinks is some universal law of nature, is only true if we use clocks that are offset from one another according to the Einstein synchronization protocol! If we use clocks that are adjusted using absolute synchronization, we would observe different travel times in different directions.
And if this all seems unbelievable, don’t blame me, I’m just the messenger. Read Einstein’s 1905 paper. It’s all right there!
Alright, I have to say before we conclude that unless you understand that a compensation for this method of clock synchronization is baked into the Lorentz transformations, in what I referred to in Episode 7.1 as the clock synchronization term,
\(\frac{vdx^\prime}{c^2} \)
then you cannot possibly understand the implications of the Lorentz transformations, nor what is really being claimed in Einstein’s special theory of relativity.
And if you care about this, then go back and read the 1905 paper and look at the Lorentz transformations, because it’ll all come together.
Alright, that’s it for now. As promised, I’ll show that special relativity becomes even less consistent in the next couple of episodes, where we’ll derive the relativistic velocity addition formula, and then show how that formula governs clock readings in the slow clock transport model.
Please write questions in the comments section below.
I’m Joe Sorge, and thanks for watching.