View references and resources for this episode.
Welcome to Ask Us Whatever. I’m Joe Sorge
Some people have questioned whether the clock-offset concept that I’ve relied on in the last two episodes is real.
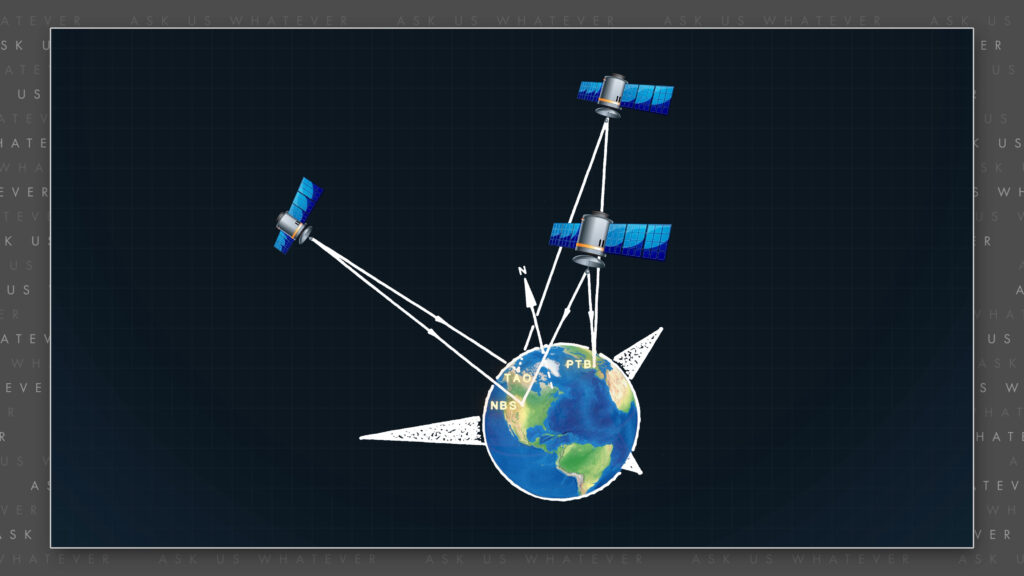
Let’s look at an article published in the journal Science in 1985 by GPS navigation experts at the National Institute of Standards, Allan, Weiss, and Ashby. The authors demonstrated the Sagnac effect between Asia, North America, and Europe, using GPS satellites and ground-based clocks.
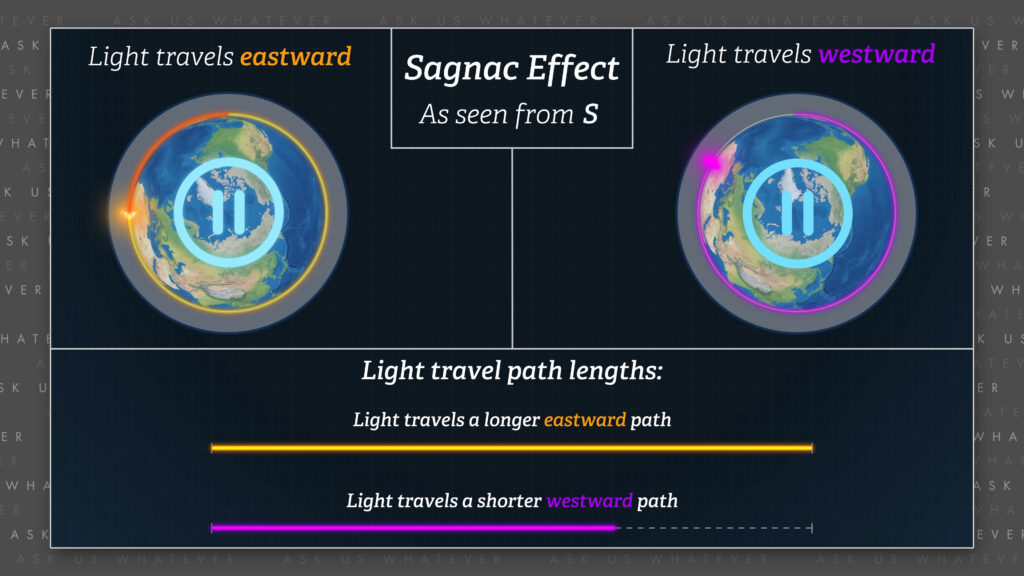
The Sagnac effect was described by Georges Sagnac in 1913. Round trip travel times along a closed loop in a reference frame in which the loop is rotating, let’s call it \(S^\prime \), take longer when light travels in the direction of rotation than when counter to the direction of rotation. If travel time is measured by a single clock located at the origin, the clock offset that can be created by Einstein clock synchronization will not factor into the measurement of travel time.

From the perspective of observers in frame \(S^\prime \), who do not know that their frame is rotating, light travels at different speeds over the same round-trip distance, since they utilize just one clock.
\(t_B-t_A \space\text{(downstream)} = \frac{r_{AB}}{(c-v)} \)
Einstein proposed in his 1905 relativity paper, that downstream travel time in frame \(S \) is equal to the distance between two points, \(r_{AB} \), divided by speed \(c \) minus the speed of the reference frame, \(v \).
\(t^\prime_A-t_B \space\text{(upstream)} = \frac{r_{AB}}{(c+v)} \)
And upstream travel time in frame \(S \) is equal to the same distance between two points, \(r_{AB} \), divided by speed \(c \) plus the speed of the reference frame, \(v \).
Clearly, when v is not zero, downstream travel time will be of greater duration than upstream travel time.
And what do we get when we divide the same distance by different travel times?
\(\frac{\text{same distance}}{\text{different times}} = \text{different speeds} \)
Different speeds! And so, when the same distance, as measured by an observer in \(S^\prime \), such as the distance around a closed loop, is divided by a longer time in one direction and a shorter time in another direction, that observer computes different speeds in the different directions.
Now this seems to contradict the second postulate of special relativity, which says that observers in all inertial reference frames will observe light to travel at a constant speed, provided, as Einstein was careful to qualify, that the clocks in any given inertial frame have been synchronized using Einstein’s clock synchronization method. And if you don’t recall that qualification, please read Section 2 of his famous 1905 relativity paper.

Now, Einstein synchronization causes clocks in the \(S^\prime \) frame to be offset by \(v \) times \(dx^\prime \) divided by \(c^2 \) seconds\(^\prime \).
In the last episode, our resurrected Einstein directed the snarky clown to adjust clock B so that clocks A and B reported different times of day by 0.87 seconds\( ^\prime \), to equalize the downstream and upstream travel times. This made it appear to observers in frame \(S^\prime \) that downstream and upstream travel times were equal, even though observers in frame \(S \) would measure different downstream and upstream travel times.

But in a closed loop with only one clock, it’s not possible to offset a single clock with itself. Essentially a closed-loop Sagnac setup removes clock synchronization variable.

But what if we look at the propagation of electromagnetic waves in a rotating frame between two points that do not complete a full, closed loop? Allan, Weiss, and Ashby state in their 1985 paper,
“If we imagine two clocks fixed a small east-west distance x apart on the Earth, then viewed from the nonrotating frame they will be moving with approximately equal speeds \(v \) equals \(\omega \) times \(r \), where \(\omega \) is the angular rotation rate of the Earth and \(r \) is the distance of the clocks from the rotation axis. If a clock synchronization process that involves electromagnetic signals were carried out by Earth-fixed observers who ignored the Earth’s rotation, then the two clocks would not be synchronous when viewed from the non-rotating frame.”
In other words, if we observe clocks in the rotating, Earth-frame, \(S^\prime \), from the perspective of the sun’s frame \(S \), and we ignore time-zone differences, Einstein-synchronized clocks would not be reporting exactly the same time, just like the example with the clown and clocks A and B in the prior episode.
The process of Einstein-clock-synchronization creates clocks that report different “times of day” as can be observed from the \(S \) frame.

Ashby wrote a definitive paper in 2003, which we have posted on our website, about the GPS system and clock synchronization. In that paper he stated:
“Simple-minded use of Einstein synchronization in the rotating frame… [of the Earth] …leads to significant error. Traversing the equator once eastward, the last clock in the synchronization path would lag the first clock by 207.4 nanoseconds. Traversing the equator once westward, the last clock in the synchronization path would lead the first clock by 207.4 nanoseconds.”
Some devoted Einsteinians seem to think that differences in clock readings in frame S’ are virtual, only real to observers in frame \(S \); and that the mathematics of the Lorentz transformations supplant reality.
Others will point out that the surface of the earth technically is not an inertial reference frame, since angular motion involves acceleration, and that this disqualifies the earth from the postulates of special relativity. Still others point out that the earth’s gravitational pull will influence clock tempo. But the centripetal acceleration of gravity is normal to the surface of the earth, and cannot explain an east to west effect parallel to earth’s surface. As pointed out by Ashby, if clocks along the equator of the Earth were to be Einstein synchronized in a full loop from west to east, the final synchronization event would demand that the first clock in the loop be pushed back in time relative to itself. And if the synchronization were to take place from east to west, the final synchronization event would demand that the first clock in the loop be pushed forward in time relative to itself. Attempting to accomplish this might be a fun concept for an art project, or for people who want to believe in special relativity, but neither gravity nor angular motion can account for this west-to-east versus east-to-west spatial gradient of clock settings.

Now a 207.4-nanosecond adjustment may not have presented a problem to Magellan, but the principles by which our GPS navigation system functions require absolute synchronization of the clocks in GPS satellites, not Einstein synchronization. There are many articles and videos describing how the GPS system works, so we’ll not get into it in detail here; but a key element to locating the position of a GPS receiver on the surface of the Earth requires the satellite clocks to be synchronized to an absolute, global time standard. Each receiver computes the differences in time signals communicated to it by several orbiting satellites, in order to compute satellite-to-receiver distances,

and those computation must use an absolute system of time. To otherwise employ an algorithm that uses Einstein synchronization of satellite-based clocks, the receivers would need to know their longitude prior to the calculation, which puts the cart before the horse.

Now you may have heard that the atomic clocks in GPS satellites need to be adjusted for the effects of special and general relativity—and that’s true. The orbital speed of the satellites causes a slowing of the atomic clocks due to time dilation, and the lower gravitational pull causes the atomic clocks to beat faster. And since the gravitational effect is larger, the net effect is that atomic clocks on-board GPS satellites beat faster than ground-based clocks, by about 38 microseconds per day.
But this impact on tempo affects all satellite-based GPS clocks and therefore, if the satellites travel at the same speed and at the same distance from the Earth’s gravitational center, time dilation and gravity cannot be responsible for different clocks reporting different times of day. Einstein’s synchronization protocol, on the other hand, produces clocks that report different times of day.
Coordinated Universal Time = UTC time
UTC time minus leap seconds = GPS time
Einstein time = GPS time minus \(v \times \frac{dx^\prime}{c^2} \)
Coordinated Universal Time, or UTC-time, and GPS-time are systems of standardized time on the Earth that do not include the offset created by Einstein synchronization. Our cell phones use GPS time, which is basically UTC time without the leap seconds.

Atomic clocks in national laboratories that keep official time around the world are coordinated using absolute synchronization, not Einstein synchronization. These clocks are synchronized absolutely with a protocol called “common-view time transfer”, which involves the transmission of a timestamp signal from a single GPS satellite to two or more ground-based atomic clocks.
Allan, Weiss, and Ashby point out that such synchronization can also be achieved by removing the amount of time computed using the clock offset term from clocks that have been Einstein synchronized. In their 1985 Science paper, they use a version of the clock offset term that we discussed in our prior episode, which takes into account the angular rate of Earth’s daily rotation, and the distance between the axis of rotation and the location of a clock on Earth’s surface.

The excellent agreement between this calculation and the common-view GPS synchronization method validates that Earth-based UTC and GPS atomic clocks are coordinated with absolute synchronization relative to the Earth, and that Einstein synchronized clocks differ by an offset amount that can be removed by re-adjusting their time by the value of the clock offset term.
In their 1985 paper, Allan, Weiss, and Ashby conducted an experiment in which they demonstrated that communication times between common-view satellites and ground-based atomic clocks were proportional to the distances between the satellites and the stations, as adjusted for the movement of the stations due to the rotation of the Earth during signal transmission from satellite to station. In other words, demonstrating that the rotation of the Earth during transmission times is consistent with the Sagnac effect when measured with Earth-based, absolutely synchronized, atomic clocks.
So, what does this all mean? Alright, now here is where I’m going to be guilty of physics blasphemy: for observers on the surface of the Earth, the time required for light to travel eastward is greater than the time required for light to travel the same distance westward. Therefore, Earth-bound observers using UTC or GPS synchronized clocks will find that light travels slower in the eastward direction and faster in the westward direction.

In the reference frame of the Earth, light speed is not constant! And that’s not just me being silly, that’s a fact that is relied upon millions if not billions of times each day by our GPS navigation devices. In order to reach the conclusion that light speed is constant in our Earth-based-reference frame, we must use Einstein-offset clocks to mask that difference in light speed, just as Einstein pointed out in postulate 2 of his 1905 relativity paper. Einstein-clock-synchronization creates an illusion of constant light speed in the moving frame. Absolute clock synchronization reveals this illusion.

Now I’m not saying that light travels through space faster in the westward direction than the eastward direction. Well maybe it will appear that way if we can absolutely synchronize our clocks relative to the barycenter of our galaxy. You know, our movement relative to the cosmic microwave background radiation most likely also biases our clocks relative to a preferred universal reference frame. But that hasn’t been demonstrated yet (Hey: Nobel prize alert! Some of you should get working on that!)
But in theory, observers in a universal, preferred reference frame will see light traveling the same speed when traveling either eastward or westward along the surface of the Earth. They will see the receiver in the east retreating from the east-bound light rays, and the receiver in the west approaching the west-bound light rays, and this will cause the differences in travel times. But they also will recognize that these differences in travel times are associated with differences in path lengths, thereby revealing that light travels at the same speed in both directions through space.
So why do physics courses teach that light travels at a constant speed in all reference frames rather than teaching that “light travels at different speeds”, and that this difference is masked when clocks are offset using Einstein clock synchronization? After all, the GPS system has been around for almost half a century, and the Allan, Weiss, and Ashby paper proved this in 1985.
I can think of two explanations. The first is that most people don’t understand the underlying facts. OK, I’m here to help! We can work this out!
We need to let go of the incorrect notion that light speed is personal—that somehow, light knows how fast we are moving and adjusts its speed for our benefit so that we can always observe light to travel at speed c. That’s a misguided interpretation of the special theory of relativity. We need to teach that the speed of light relative to any reference frame will vary depending on the speed of the reference frame, but that Einstein clock synchronization will cause the calculation of light speed to be constant due to the way the clocks have been synchronized.

Interestingly, I will show in a future episode that if two clocks are held side-by-side and synchronized exactly, time dilation will cause their readings to drift apart if the two clocks are slowly moved to different locations.
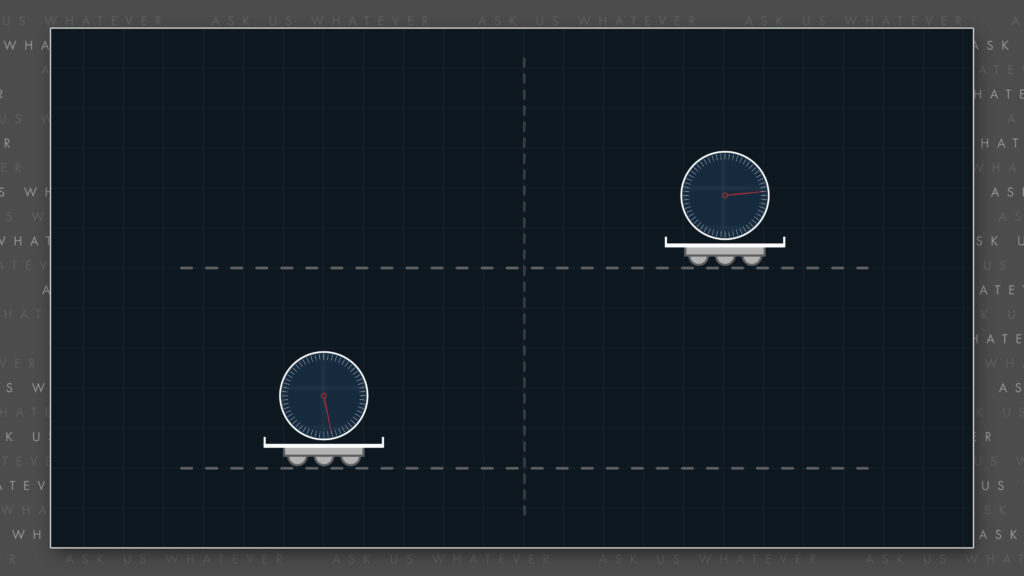
If the clocks are moved slowly, the amount of drift will equal the amount of clock offset resulting from Einstein’s clock synchronization protocol. In other words, clocks will naturally become offset by an amount consistent with the clock-offset term of the Lorentz transformations, simply due to differential time dilation. So, unless clocks are absolutely synchronized, such as by using GPS satellites, they will naturally be in a state that causes the measurement of light speed to erroneously appear to be constant. Prior to the invention of GPS satellites and common-view synchronization protocols, light speed would always erroneously appear to be constant. But now we know: that was an artifact.
Yet physicists prefer to say that the Sagnac effect is caused by differential path lengths, rather than differential light speed covered up by oddly synchronized clocks. This probably results from their incomplete understanding of the second postulate of special relativity.

OK, if I say any more, I might get banned from PhysBook or Phitter, but if you really want to be honest about The Special Theory of Relativity, then you should teach physics students that light travels at different speeds when measured with absolutely synchronized, atomic clocks, yet this is obscured when using Einstein synchronized clocks.
Alright, that’s it for now! If you have any questions, please write them in the comments sections. I’m Joe Sorge, and thanks for watching.