Welcome to Ask Us Whatever. I’m Joe Sorge.
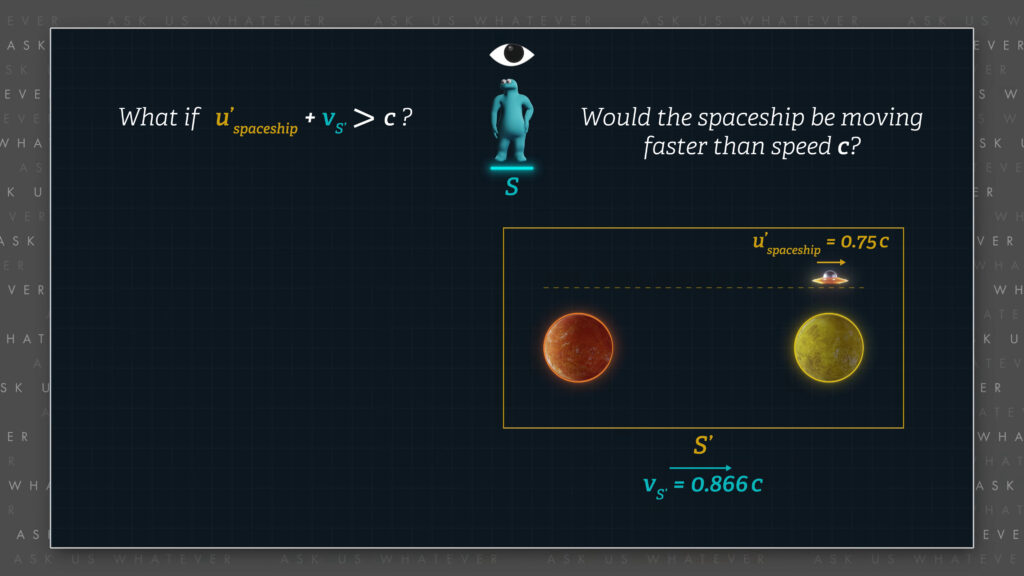
Einstein was faced with a conceptual challenge. What happens if a spaceship moves at some speed approaching speed \(c \) while traveling within an inertial reference frame, call the Frame \(S’ \), that is also moving at a very high speed in the same direction, as measured relative to another frame, call that Frame \(S \)?

What if the two speeds add up to more than \(c \)? Would the spaceship be moving faster than speed \(c \) with respect to an observer in Frame \(S \)?
As you may recall the Lorentz gamma factor is equal to one divided by the square root of one minus \(v \) squared over \(c \), where \(v \) is the difference in speed between frames \(S \) and \(S’\).
\(\gamma_L = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} \)
What if instead of considering the spaceship to be moving within Frame \(S’ \), we considered the spaceship to be stationary within another frame that we’ll call \(S’’ \) (S double prime) that is moving at a speed equal to the sum of the original speed of Frame \(S’ \) relative to Frame \(S \), plus the original speed of the spaceship within Frame \(S’ \)?
In that case the speed of Frame \(S’’ \) relative to Frame \(S \) would be greater than \(c \), and the denominator of the Lorentz gamma factor would become an imaginary number.
This creates a serious problem, as we will learn in a future episode, because Einstein predicted that the total energy of an object, as viewed by a stationary observer, is equal to the Lorentz gamma factor times the rest mass of the object, \(m \), times its speed squared.
\(E = \gamma_Lmc^2 \)
If speed \(v \) equals speed \(c \), the denominator of the Lorentz gamma factor becomes equal to zero, and the Lorentz gamma factor blows up to infinity!
Which would mean that any massive object traveling at speed \(c \) would have infinite energy. Not just a lot of energy but all of the energy of the universe (\(∞ \)), maybe more!
Einstein proposed a solution to this problem by deploying the Lorentz transformations. He took the Lorentz transformation for \(dx \) and divided it by the Lorentz transformation for \(dt \) to compute the speed of the of the spaceship, \(dx/dt \), as seen from the stationary Frame \(S \).
\(dx = \gamma_Ldx’ + \gamma_Lvdt’ \)
\(\frac{dx}{dt} = \frac{\gamma_Ldx’+ \gamma_Lvdt’}{\gamma_Ldt’ + \frac{\gamma_Lvdx’}{c^2}} \)
He simplified this expression by dividing both the numerator and denominator by the Lorentz gamma factor times \(dt’ \) (\(\gamma_L x dt’ \)),
\(\frac{dx}{dt} = \frac{\frac{\gamma_Ldx’}{\gamma_Ldt’}+\frac{\gamma_Lvdt’}{\gamma_Ldt’}}{\frac{\gamma_Ldt’}{\gamma_Ldt’} + \frac{\gamma_Lvdx’}{\gamma_Ldt’c^2}} \)
\(\frac{dx}{dt} = \frac{\frac{dx’}{dt’} + v}{1 + \frac{vdx’}{dt’c^2}} \)
and then simply renamed the \(dx’/dt’ \) speed of the spaceship within the moving frame, \(u’ \).
\(u’ = \frac{dx’}{dt’} \)
So, the relativistic velocity addition formula can be written as, \(u’ \) plus \(v \) divided by one plus \(v \) times \(u’ \) over \(c-squared \). For further simplicity, we can call the stationary-frame relativistic velocity, \(u \).
relativistic velocity \(= \frac{dx}{dt} = u = \frac{u’+v}{1+\frac{vu’}{c^2}} \)
Ok, let’s just check it out with an example in which the spaceship is traveling at 75% of \(c \) within a reference Frame \(S’ \) that is traveling at 86.6% of \(c \). We get about 98% of speed \(c \).
\(u = \frac{0.75 + 0.866}{1 + \frac{(0.866)(0.75)}{1^2}} ≈ .98c \)
You can try other examples, but if \(u’ \) and \(v \) are less than or equal to \(c \), then the additive speeds will always be less than or equal to \(c \).

Now, let’s ask what happens if a stationary observer in Frame \(S \) sees two spaceships heading toward each other, each traveling at 75% of \(c \) relative to Frame \(S \).
Does the stationary observer see their relative speed as 150% of \(c \)? The answer is yes. Einstein’s model allows the normal, linear addition of speeds when each speed is measured by an observer in a third reference frame. But if that observer were to be traveling within one of those spaceships, then, according to Einstein, the observer would not perceive the other spaceship to be approaching at 150% of \(c \). Instead, Einstein would have the observer use the velocity addition formula to compute relative speed.
Now that may seem a little confusing, so just remember that if both speeds are measured independently, from a single frame, which we are calling Frame \(S \), then the speeds can be added linearly. But if one speed is measured from Frame \(S \) and another speed is measured from Frame \(S’ \), then they must be added using the velocity addition formula.
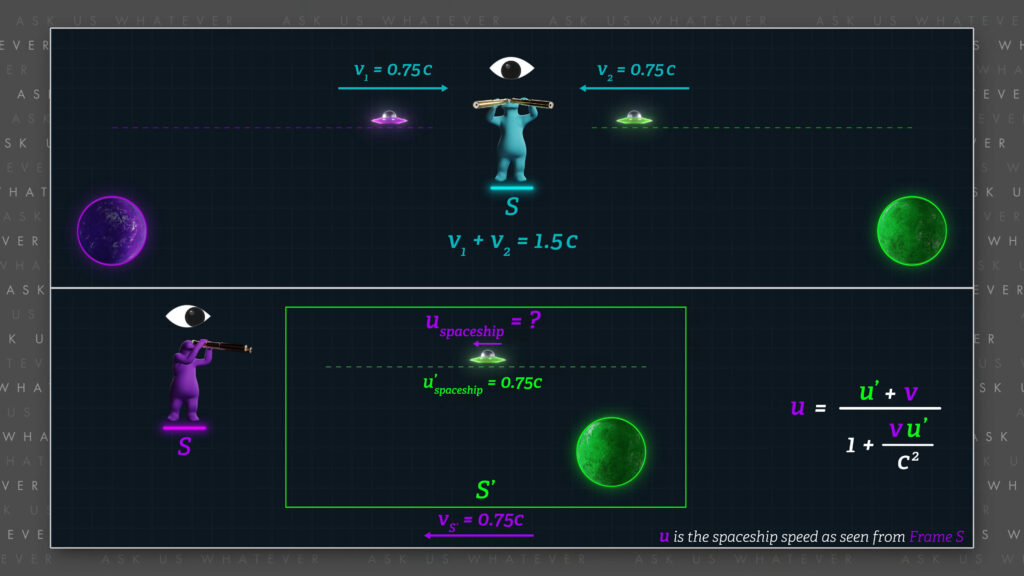
This is another way of saying that, in Special Relativity, no single object can be measured to travel, with respect to a given reference frame, at a speed equal to or exceeding \(c \), especially since its energy would be infinite as viewed by observers in that frame.
OK, up to now I’ve recited textbook doctrine, which you can find on a hundred other YouTube videos. But, as you know, I have a tendency to poke the tiger, so let’s explore this one further.
Let’s go back to the spaceship traveling at 75% of \(c \) within a reference Frame \(S’ \) moving at about 86.6% of \(c \) with respect to reference Frame \(S \). I chose 86.6% of \(c \) since the Lorentz factor is equal to about 2 at that speed, which makes the math easier to follow.
What does 75% of \(c \) within Frame \(S’ \) really mean? (a beat) It’s the speed at which observers in Frame \(S’ \) would think the spaceship was moving if they didn’t know that Frame \(S’ \) was moving. That speed, which we’ll label \(u’ \), is measured in units of proper \(meters’ \) per proper \(second’ \). In other words, \(meters’ \) are measured with the meter sticks of Frame \(S’ \) (according to Special Relativity, these meter sticks will look contracted to observers in Frame \(S \)), and \(seconds’ \) are measured with the clocks of Frame \(S’ \) (these clocks will appear to beat slower to observers in Frame \(S \) and will be offset according to the Einstein clock synchronization). 75% of \(c \) in Frame \(S’ \) is about 225 million frame-\(S’ \) \(meters’ \) for every \(second’ \) of spaceship travel.
Let’s turn that into a speed in the stationary frame, and add it to the 86.6% of \(c \) speed of Frame \(S’ \) relative to Frame \(S \), to see if we get 98% of \(c \).
According to Special Relativity, length contraction of reference Frame S’, at 86.6% of \(c \), shrinks the \(dx’ \) distance traveled by the spaceship within reference Frame \(S’ \), from about 225 million Frame \(S’ \) \(meters’ \) down to about 112.5 million stationary Frame \(S \) meters. And 1 proper \(second’ \) gets converted by time dilation to 2 stationary Frame Seconds. So, we would naively think that the spaceship would appear to observers in Frame \(S \) to be moving at 56.25 million meters during every stationary Frame Second, in addition to the speed of Frame \(S’ \) relative to Frame \(S \).
\(\frac{\text{112.5 million meters}}{\text{2 seconds}} = \text{56.25 million meters per second} \)
And since Frame \(S’ \) is moving about 0.866 x 300 million meters per second, which is about 260 million meters per stationary second, we can add these speeds together to get,
\(56.25 + 260 = \text{316.25 million meters per stationary second} \)
Uh, oh – 316.25 million meters per stationary second? That’s about 105% of light speed \(c \), not 98%. Oops.

What did we do wrong? We performed the length contraction properly, so that should be ok. And we simply converted 1 moving frame \(second’ \) to 2 stationary frame seconds, according to time dilation, which seems correct. So, what went wrong?
Well, we forgot that we also needed to factor in, wait for it — the effect of Einstein clock synchronization! We, naively thought that 1 second’ is really 1 \(second’ \). How foolish of us? But not in Einstein’s world!
For purposes of converting Frame \(S’ \) time to Frame \(S \) time, we must adjust 1 \(second’ \) by the amount that the downstream clock in Frame \(S’ \) had been adjusted backwards when Einstein clock synchronization was performed on the clocks in Frame \(S’ \). In other words, during clock synchronization, light’s travel time in the downstream direction is of longer duration than 1 \(second’ \), but the effect of Einstein clock synchronization causes the downstream clock to read an earlier “time of day” than the upstream clock; and so, the downstream clock “under-reported” the amount of time that had elapsed.
We must therefore add the “under-reported” time back, via the stationary frame version of the clock offset term of the Lorentz transformations, when computing \(dt \).
\(\gamma \frac{vdx’}{c^2} \)
If that is not entirely clear, you may want to watch Episodes 7.2 and 7.3 on Einstein clock synchronization for a refresher; but if you fully understand Einstein clock synchronization, in which case you’re as nutty as me, let’s press on.
Let’s confirm that the clocks in Frame \(S’ \) must report different readings at different locations in order for the manual computation of spaceship speed to equal the speed computed by Einstein’s velocity addition formula. In our example, the spaceship travels through Frame \(S’ \) at 75% of speed \(c \). Which means that if the spaceship travels a distance of 0.75 light-\(seconds’ \) in 1 \(second’ \) time (which is about 225 million proper \(meters’ \) in the \(S’ \) Frame in 1 \(second’ \) time), a Frame \(S’ \) clock at the end of this 0.75 light-\(second’ \) trip will report a time to the passenger in the spaceship at the end of their trip that is 1 \(second’ \) later than those passengers observed on clock \(A’ \) at the beginning of their trip. This is what is meant when we say that an object travels at 75% of \(c \) for one \(second’ \) in Frame \(S’ \).
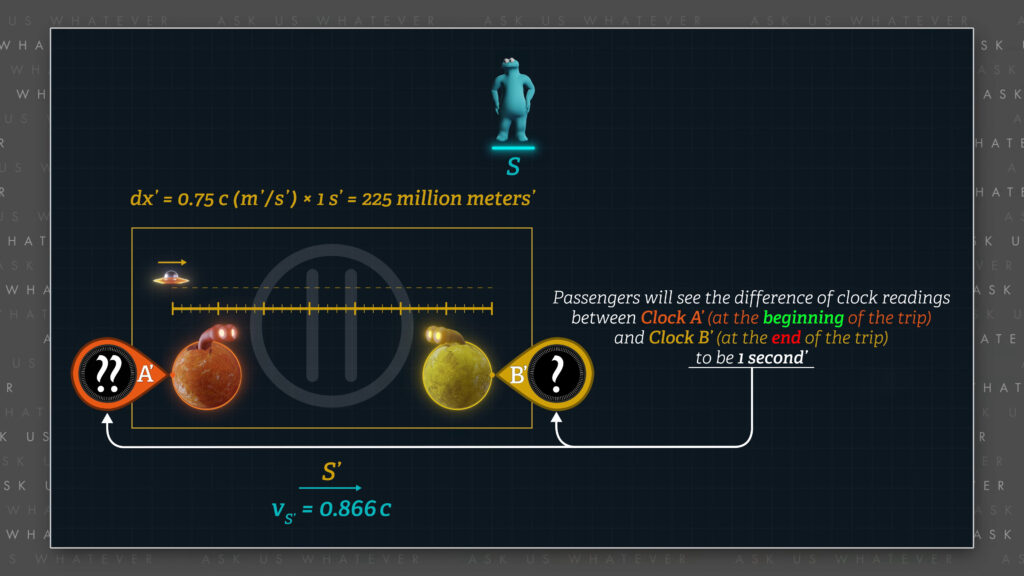
According to Einstein’s 1905 relativity paper, which we analyzed in Episode 7.2, clocks at a distant location are synchronized using light signals. Einstein approached this by computing the number of Frame \(S \) seconds required for light to travel from an upstream clock to a downstream clock, and then back again to the upstream clock.
In our current spaceship example, our clocks of interest in Frame \(S’ \) are separated by 0.75 light-\(seconds’ \). Recall that Frame \(S’ \) moves with respect to Frame \(S \) at 86.6% of speed \(c \). So according to Einstein, the amount of Frame \(S \) time required for a light signal to travel from the upstream clock to the downstream clock is, the distance separating clocks \(A’ \) and \(B’ \), which is \(dx’ \) divided by a factor of gamma (to account for length contraction) all divided by \(c \) minus \(v \).
This is equal to 2.8 Frame \(S \) seconds.
\(\text{dt}_{downstream} = t_B – t_A = \frac{r_{ab}}{c-v} = \frac{\frac{dx’}{\gamma_L}}{c-v} = \frac{\frac{0.75}{2}}{1-0.866} ≈ \text{2.8 seconds} \)
\(\text{dt}_{downstream} = t_{B’} – t_{A’} \)
\(\text{dt}_{downstream} = \frac{r_{A’B’}}{c-v} \)
\(\text{dt}_{downstream} = \frac{\frac{dx’}{\gamma_L}}{c-v} \)
\(\text{dt}_{downstream} = \frac{\frac{0.75}{2}}{1-0.866} ≈ \text{2.8 seconds} \)
And the amount of time for light to make the return journey would be, 0.2 Frame \(S \) seconds.
\(\text{dt}_{upstream} = t’_A – t_B = \frac{\frac{0.75}{2}}{1+0.866} ≈ \text{0.2 seconds} \)
\(\text{dt}_{upstream} = t’_{A’} – t_{B’} \)
\(\text{dt}_{upstream} = \frac{r_{B’A’}}{c+v} \)
\(\text{dt}_{upstream} = \frac{\frac{dx’}{\gamma_L}}{c+v} \)
\(\text{dt}_{upstream} = \frac{\frac{0.75}{2}}{1+0.866} ≈ \text{0.2 seconds} \)
Now remember, Einstein wants these downstream and upstream travel times to appear to be equal in Frame \(S’ \) in order to satisfy his definition of clock synchronization and to force light speed to be constant in all directions.
Recall that the clocks in the \(S’ \) frame beat at half the rate of the clocks in Frame \(S \) due to the speed of Frame \(S’ \) with respect to Frame \(S \), and so the equivalent downstream time elapsed in Frame \(S’ \) will be, 1.4 \(seconds’ \).
\(dt’_{downstream} = t_{B’} – t_{A’} = \frac{\text{2.8 seconds}}{\frac{\text{2 seconds}}{second’}} = \text{1.4 seconds}^\prime \)
And the equivalent upstream time elapsed in Frame \(S’ \) will be, 0.1 \(seconds’ \).
\(dt’_{upstream} = t’_{A’} – t_{B’} = \frac{\text{0.2 seconds}}{\frac{\text{2 seconds}}{second’}} = \text{0.1 second}^\prime \)
In other words, all of the clocks in Frame \(S’ \) advance half as many \(seconds’ \) as compared to all of the clocks in Frame \(S \). Clock synchronization does not affect clock tick rate, merely the “time of day” reported by each clock. And since Einstein clock-synchronization requires the downstream and upstream measurements of light’s travel time to be equal in Frame \(S’ \), the “time of day” reported by downstream clock \(B’ \) must be adjusted. Clock \(B’ \)’s reported time must be offset to an earlier “time of day” than the time of day reported by the upstream clock \(A’ \), by 0.65 \(seconds’ \).
This will make it appear to observers in Frame \(S’ \) that the downstream and upstream clocks are doing what Einstein wants them to be doing, because the measured time for light to travel from clock \(A’ \) to clock \(B’ \) will be 0.75 \(seconds’ \);
\(dt’_{\text{adjusted downstream}} = 1.4 – 0.65 = 0.75 seconds’ \)
and the measured time for light to travel from clock \(B’ \) back to clock \(A’ \) will also be, 0.75 \(seconds’ \).
\(dt’_{\text{adjusted upstream}} = 0.1 + 0.65 = 0.75 seconds’ \)
So, when two, Frame \(S’ \) clocks are separated by 0.75 light-\(seconds’ \), the downstream clock must be offset to report a time of day that is 0.65 \(seconds’ \) earlier than the upstream clock, as can be observed from Frame \(S \). And since at 86.6% of \(c \), the Lorentz gamma factor is equal to 2, this 0.65 \(second’ \) offset between clocks will be the equivalent to 1.3 Frame \(S \) seconds.

Interesting! Right? This agrees exactly with the second term of the Lorentz \(dt \) transformation!
The second term of the Lorentz \(dt \) transformation is, the Lorentz gamma factor times the speed of Frame \(S’ \) with respect to Frame \(S \), \(v \), times the separation of the two clocks in Frame \(S’ \), \(dx’ \) \(meters’ \), divided by \(c \) squared.
\(\text{2nd term in L’s dt transformations | clock offset} = \frac{\gamma_L v}{c^2}dx’ \)
In our example, this is equal to, approximately 1.3 seconds.
\(\text{2nd term in L’s dt transformations | offset} = 2 \times 0.866 \times \frac{0.75}{1^2} ≈ 1.3 seconds’ \)
Is that a coincidence? Heck NO!
The Lorentz transformations anticipate that the readings of the clocks in Frame \(S’ \) follow a spatial gradient along the axis of motion. The second term of the Lorentz \(dt \) transformation adds back the difference between the readings of clocks separated by a distance of \(dx’ \) in the \(S’ \) Frame and converts that difference to stationary frame seconds.
And so, when we attempt to compute the speed of the spaceship, as observed by observers in Frame \(S \), we must recognize that the times observed by observers in Frame \(S’ \) are distorted by the adjustments that had been made to their clocks when those clocks were Einstein synchronized; and we have to reverse those adjustments to translate Frame \(S’ \) \(seconds’ \) into seconds, using the second term of the Lorentz \(dt \) transformation.
\(\text{2nd term in L’s dt transformations | clock offset} = \frac{\gamma_L v}{c^2}dx’ \)
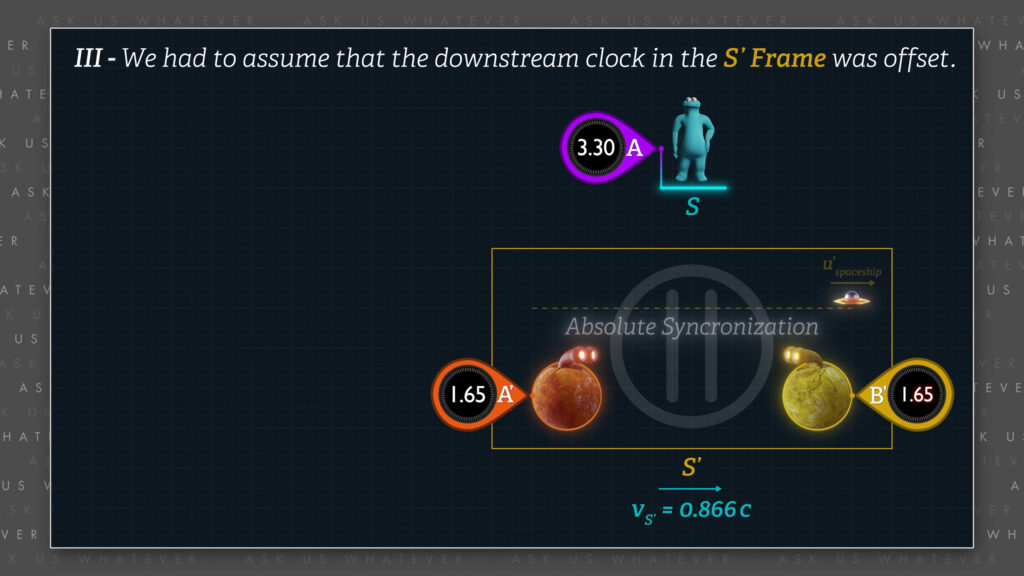
If the clocks in Frame \(S’ \) had not been Einstein-synchronized, but instead had been absolutely synchronized, then the difference in readings between the Frame \(S’ \) upstream and downstream clocks at the beginning and end of our spaceship’s 0.75 light-\(second’ \) trip would have been 1.65 \(seconds’ \) instead of 1 \(second’ \)!
\(\text{difference in reading} = 1 \text{second}’ + \frac{1.3 seconds}{\gamma second/second’} = 1 + \frac{1.3}{2} = 1.65seconds’ \)
See Episode 7.3 if you’d like a refresher on how our GPS navigation systems use absolutely synchronized clocks.
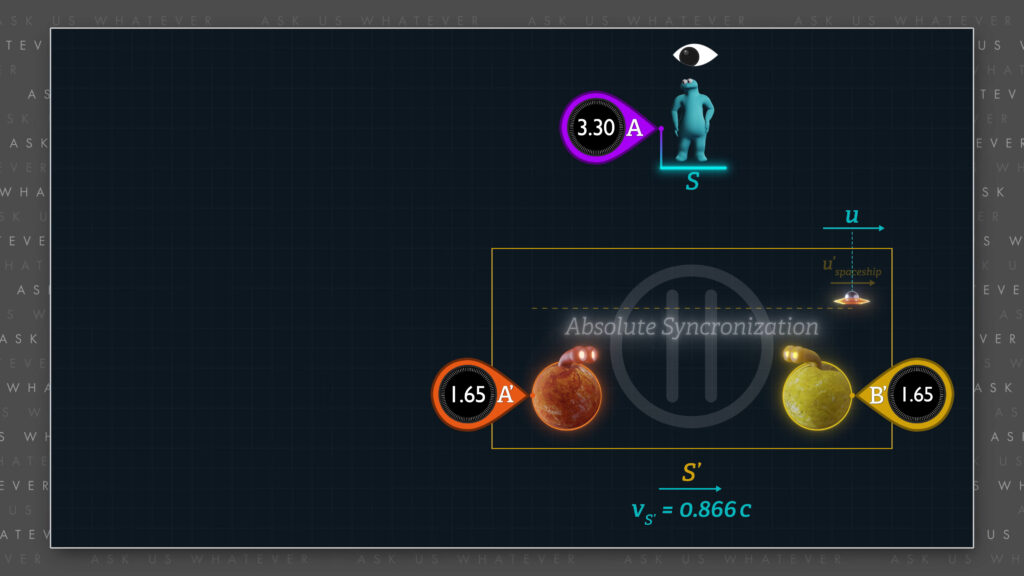
But with Einstein clock-synchronization, the observers in Frame \(S’ \) measure an elapsed time of only 1 \(second’ \) due to the differential readings of the upstream and downstream clocks. And as a reminder, that’s the trick that Einstein uses to keep the speed of light constant in all reference frames.
So, if we use clocks that have been Einstein synchronized, elapsed time as measured in Frame \(S’ \) will be 1 \(second’ \), and total elapsed time as measured from Frame \(S \) will be calculated using the Lorentz \(dt \) transformation, where we add back the missing 1.3 seconds resulting from the way that the clocks in Frame \(S’ \) had been offset.
\(\text{dt seconds} ≈ \gamma \times \text{1 second}’ + \gamma \frac{0.866×0.75}{c^2} ≈ \text{3.3 seconds} \)
\(\text{dt seconds} ≈ \text{2 seconds} + \text{1.3 seconds} ≈ \text{3.3 seconds} \)
Now let’s now compute the speed of the spaceship within Frame \(S’ \), as seen from Frame \(S \), using 3.3 stationary Frame Seconds as the time required to travel a length-contracted 0.75 light-\(seconds’ \), which gives us about 34 million meters per second.
\(\text{ship’s speed}_{\text{seen from S}} = \frac{\text{112.5 million meters}}{(2 + 1.3) seconds} = \text{34 million meters per second} \)
And if we add that to our Frame \(S’ \) speed, \(v \), of 260 million meters per second we get the 98% of speed \(c \), as obtained with Einstein’s velocity addition formula.
\(34+260=\text{294 million}\frac{meters}{second}≈98\%c \)
Whew! That was a lot of work! But it was worth it, because we got to see the postulates and premises behind Special Relativity and the Lorentz transformations in action. And we showed that the clocks in Frame \(S’ \) must report different times of day depending on their location along the axis of motion, since we needed to compensate for this spatial gradient of clock readings in order to be in agreement with Einstein’s velocity addition formula.
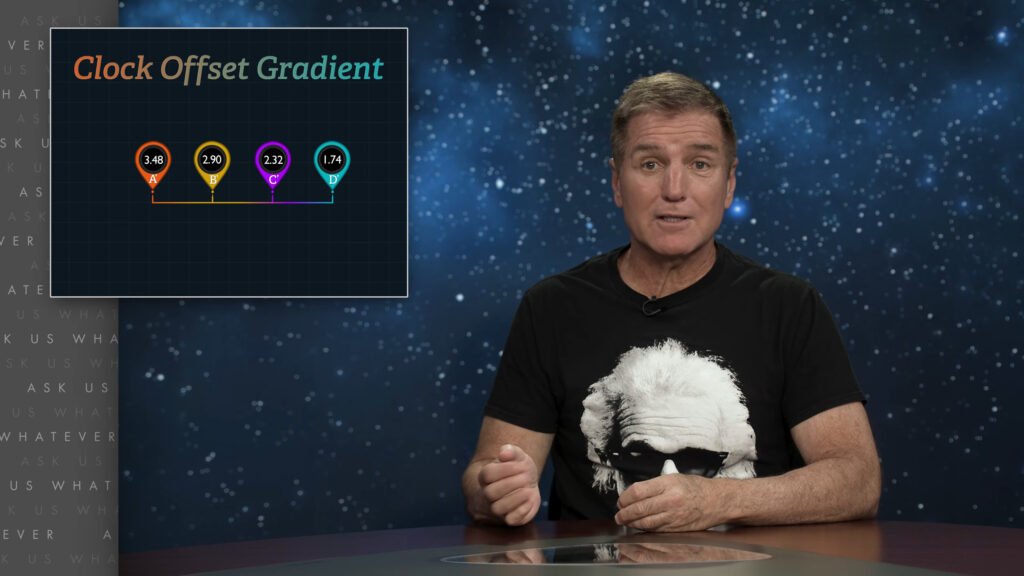
Without reversing the spatial gradient of Frame \(S’ \) clock readings, the sum of the velocities would have exceeded speed \(c \). Einstein clock-synchronization creates the equivalent of a continuum of infinitesimally small time zones in which the clocks have been adjusted to match the location of the time zone along the axis of motion. This is not a virtual effect in Special Relativity! It needs to be real and it is why light is perceived to travel at a constant speed relative to this array of differential clock readings.
Alright, let’s summarize the somewhat farfetched things that we had to do to arrive at a speed that conforms to Einstein’s velocity addition formula:
- 1. We had to assume that the proper distance traveled by the spaceship in its own frame of reference, \(dx’ \), would physically contract by a factor of gamma as observed from the stationary frame. This means that the distance contribution coming from the \(dx’ \) distance in Frame \(S’ \) must be shrunken when accounting for it in Frame \(S \). I think this is implausible; and I’m being kind.
- 2. We had to assume that time dilates by a factor of gamma in order to partially compute \(dt \) from \(dt’ \). I agree that time dilates, but I think the Lorentz factor is a special case conversion factor, and that gamma (\(s \)), as defined in Episode 6.1, is the general case conversion factor that we really should use.
- 3. We had to assume that the downstream clock in the \(S’ \) Frame was offset during Einstein clock synchronization, which caused the observers in the spaceship to be persuaded into thinking that they had traveled for only 1 \(second’ \), when absolutely synchronized clocks would have documented their travel time to have been 1.65 \(seconds’ \); and therefore we had to add an additional 0.65 clock-offset \(seconds’ \) to their Einstein adjusted, 1 \(second’ \) travel time in order to compute the speed of the spaceship as observed from Frame \(S \).
- 4. In order to compute stationary frame elapsed time, we also needed to inflate those 0.65 \(seconds’ \) to 1.3 stationary seconds, and add those 1.3 stationary seconds to the 2 stationary seconds that we obtained when we reversed the time dilated 1 \(second’ \) that was measured by the Frame \(S’ \) observers, and then divide the length-contracted \(dx’ \) distance by 3.3 stationary seconds instead of 2 stationary seconds!
- 5. We needed to add that converted spaceship speed to the moving reference Frame Speed in meters per second to arrive at the final velocity addition speed.
- 6. And we needed to cross our fingers and hope that speed \(v \) that we used to compute the Lorentz gamma factor was meaningful.
I want to remind you that in Special Relativity, speed \(v \) is the difference between the speed of one reference frame versus some second reference frame carrying an observer with whom we can eventually communicate. Special Relativity would have us believe that lengths contract, times dilate, and clocks adjust themselves in Frame \(S’ \) in response to any random observer in any random inertial reference frame. And as I’ve emphasized before, this becomes impossible when we try to accommodate the constraints imposed by two different observers in two different reference frames.

So, the math behind Einstein’s velocity addition is more complicated and contrived than it first appears. No wonder people either really don’t understand Special Relativity, or just accept it as doctrine to avoid the brain damage of unraveling it. We obviously need to fix that. And so, we’ll begin to steer back toward reality in the next episode, where we cover the alternative model velocity addition formula.
Alright, if you have any questions, please write them in the comments section. I’m Joe Sorge, and thanks for watching.



