Hey! Welcome to Ask Us Whatever, I’m Joe Sorge.
In 1859 Hippolyte Fizeau reported the results of a very interesting experiment.
He passed light through moving water in opposite directions and asked whether the speed of the wave fronts was altered by the speed of the water.
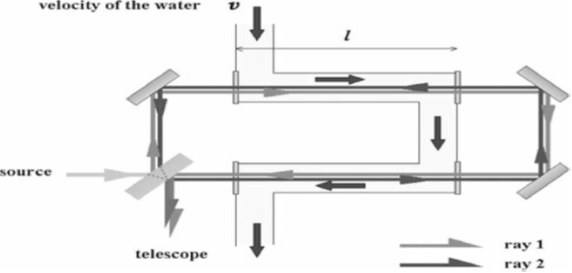
Prior to Fizeau, it was known that light traveled more slowly through stationary water as compared to its speed through air or vacuum. The ratio of the speed of light through vacuum divided by the speed of light through a particular medium is called the refractive index, \(n \).
\(refractive\ index=n=\frac{speed\ through\ vacuum}{speed\ through\ medium} \)
For water, the value of \(n \) is about 1.333 and varies slightly with the wavelength of light. This slight variation is what causes us to see different colors in the rainbow. But for simplicity, we can generalize the speed of light through stationary water to be about, 75% of its speed through vacuum.
\(speed\ of\ light\ through\ water\ \approx\frac{c}{n}\approx\frac{c}{1.333}\approx0.75c \)
Fizeau wanted to answer a very interesting question about what scientists in the 19th century called the luminiferous ether, which they envisioned to be a hypothetical medium through which light waves travel. They speculated that if water were to fully drag the “ether”, then the speed of light through moving water would be the speed of light through stationary water, \(\frac{c}{n} \), plus or minus the speed of the water.
\(u(fully\ dragged)=\frac{c}{n}\pm w \)
But if the luminiferous ether was not dragged by the moving water, they proposed that light speed would merely equal \(\frac{c}{n} \), regardless of the speed of the water.
\(u_{no\ drag} = \frac{c}{n} \)
Fizeau’s experiment yielded neither result.
Fizeau found that the speed of light through moving water was approximately, \(\frac{c}{n} \) plus or minus the speed of the water multiplied by 1 minus 1 over the refractive index squared, adding or subtracting slightly less than half the speed of the water to the speed of light through stationary water.
\(u=\frac{c}{n}\pm w(1-\frac{1}{n^2})\approx c/n\pm0.437w \)
Fizeau’s result was difficult to explain; although the result remarkably agreed with an experiment done in 1810 by Francois Arago using glass prisms placed in front of a telescope. Arago’s result was later re-examined by Augustin-Jean Fresnel who proposed a “partial ether drag” hypothesis in which a refractive medium partially drags the luminiferous ether in proportion to one minus one over \(n \) squared.
\(1-\frac{1}{n^2} \)
The partial ether drag hypothesis was not very popular in the early 1800s, but when Fizeau arrived at the same answer with moving water, scientists had to consider it seriously.
There were few new ideas on the subject until Einstein came along. Einstein claimed that Fizeau’s experiment provided one of the most influential elements in the development of his Special Theory of Relativity in 1905. He never clearly articulated why the Fizeau result was so important to him, but Einstein was not a fan of the luminiferous ether and Fizeau’s result seemed to refute simple ether theory.
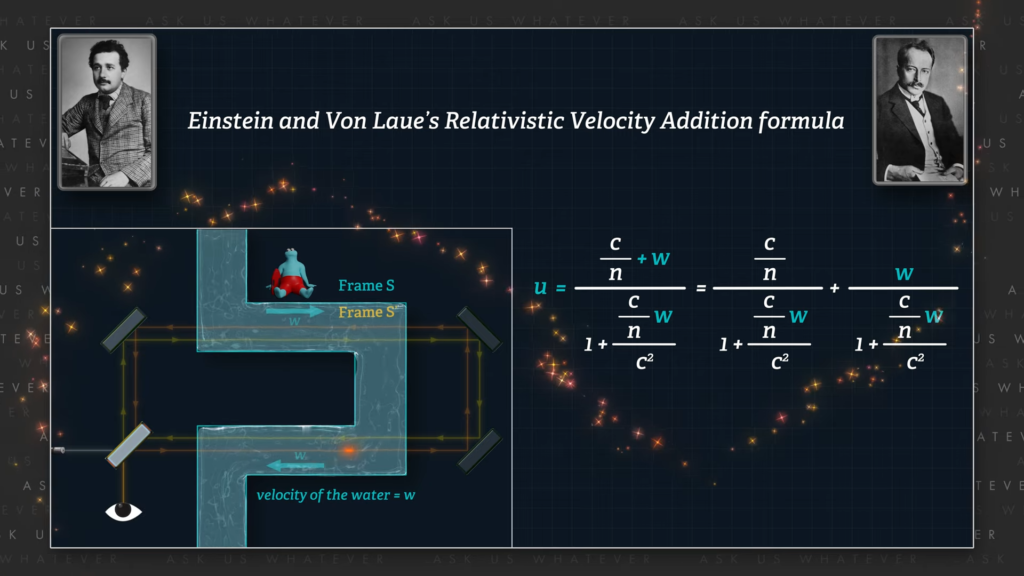
And then in 1907 Max von Laue proposed an explanation of the Fizeau result, involving Einstein’s 1905 velocity addition formula. And although we covered that formula in Episode 9.1, let’s do a quick refresh here.
Einstein derived this formula by taking the ratio of two Lorentz transformations, \(dx \) divided by \(dt \).
\(u=\frac{dx}{dt} \)
\(u=\frac{\gamma_L\left(dx^\prime+vdt^\prime\right)}{\gamma_L\left(dt^\prime+\frac{vdx^\prime}{c^2}\right)} \)
By dividing numerator and denominator by the Lorentz gamma factor times \(dt^\prime \), one obtains, \(u^\prime \) plus \(v \) all divided by 1 plus \(v \) times \(u^\prime \) over \(c \) squared, where \(u \) is the combined relativistic velocity as observed from the laboratory Frame \(S \), \(u^\prime \) represents \(\frac{dx^\prime}{dt^\prime} \) which is the speed of something (like light) as measured from the perspective of observers in Frame \(S^\prime \) (like observers moving with the water), and \(v \) is the speed of Frame \(S^\prime \) relative to the laboratory Frame \(S \).
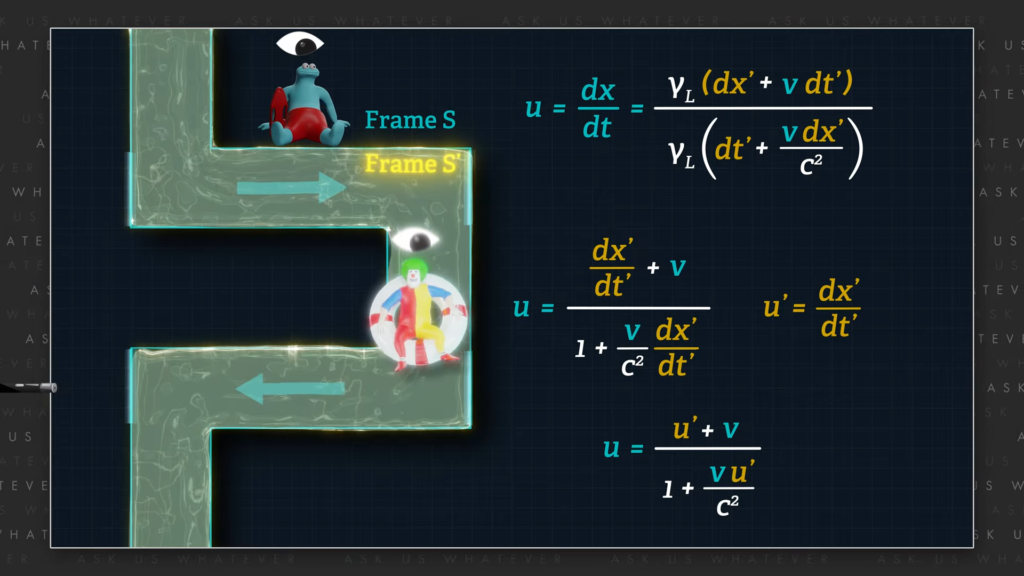
\(u=\frac{\frac{dx^\prime}{dt^\prime}+v}{1+\frac{v}{c^2}\frac{dx^\prime}{dt^\prime}} \)
\(u=\frac{u^\prime+v}{1+\frac{vu\prime}{c^2}} \)
Von Laue proposed that the speed of the water, \(w \), is like speed \(v \) of Frame \(S^\prime \) relative to Frame \(S \) and that \(u^\prime \) is the speed of light passing through water as measured from the perspective of Frame \(S^\prime \), in other words from the perspective of the water.
Von Laue proposed that since the speed of light through stationary water is \(c \) divided by \(n \) when \(w \) is zero. \(u^\prime \) would also be equal to \(c \) divided by \(n \) in the water’s Frame \(S^\prime \).
\(u_0=\frac{c}{n}\ meters\ per\ second,\ when\ w=0 \)
\(u^\prime\left(vonLaue\right)=\frac{c}{n}meters^\prime per\ second^\prime \)
In other words, he proposed (incorrectly) that the Theory of Relativity would require light to be measured at the same numerical speed in either Frame \(S \) or in Frame \(S^\prime \).
His logic resulted in a modified velocity addition formula, predicting that speed \(u \), the speed of light through water as measured in the laboratory Frame \(S \), would be equal to \(c \) divided by \(n \) plus or minus \(w \), all divided by 1 plus or minus \(w \) over \(n \) times \(c \); which to first order approximation is, \(c \) divided by \(n \), plus or minus the speed of the water medium, \(w \), times the quantity 1 minus 1 over \(n^2 \).
\(u=\frac{\frac{c}{n}\pm w}{1\pm\frac{w}{nc}}\approx\frac{c}{n}\pm w\left(1-\frac{1}{n^2}\right) \)
That is, the first order approximation to von Laue’s formula appears to equal the Fresnel/Fizeau formula for light speed through refractive media.
\(u_{Fizeau} \approx \frac{c}{n} \pm w(1- \frac{1}{n^2}) \)
This was touted to be proof that Special Relativity was a valid theory and additional proof that there was no luminiferous ether. Many physicists soon believed that light’s speed through a moving, refractive medium was merely the relativistic sum of the speed of the medium plus light’s speed through the refractive medium when stationary.
Most textbooks involving Special Relativity have incorporated von Laue’s interpretation of Fizeau’s result as proof that Special Relativity is valid. Physics journals consider this to be “settled science”.
Well, I intend to show you now that there is another, more plausible explanation to the Fresnel/Fizeau finding, and that it need not involve Special Relativity at all. In fact, the invocation of Special Relativity to explain the Fizeau result is a perfect example of enthusiasm for a new theory (in the early 1900s) working together with confirmation bias and group-think to yield unsupported conclusions. Conclusions that have remained in physics textbooks up to now.
So let’s lay down a foundation and some definitions so we can develop a new model, and then we’ll compare it to von Laue’s Special Relativity formula.
We’ll start with simple Galilean relativity for now. That is, no time dilation and no length contraction.
I generally use the label capital S to signify what I jokingly call the inertial reference frame of the cosmic train station.

This represents the presumed stationary frame of the universe. Von Laue instead chose to consider Fizeau’s laboratory as being stationary, even though it resides on the Earth which we know rotates every 24 hours, whizzes around the sun at 30,000 meters per second, and moves together with the sun through the universe. Nevertheless, we will go along with von Laue for now and assume that Fizeau’s Earth-based laboratory represents stationary Frame S, and that the moving water in Fizeau’s experiment will be reference Frame S’.
light speed through refractive media = \(\frac{c}{n} meters_{earth} / second_{earth} \)
The argument made in favor of n being independent of speed, is that light traveling through refractive media on the Earth seems to travel at the same speed regardless of the time of day or the physical orientation of the media – in other words regardless of the media’s orientation with respect to Earth’s orbit around the sun. So, we’ll run with von Laue’s approximation, that light will travel at approximately c divided by n in slowly moving water.
\(u’ = \text{light in speed in slowly moving water} \approx \frac{c}{n} meters’_{\text{moving water}}/seconds’_{\text{moving water}} \)
We will say that reference Frame S’, and the water within it, both move at speed w meters per second as measured from Frame S.
Let’s label distances traveled in the Laboratory Frame S with the term “dx” and label times measured in the Laboratory Frame using the term “dt”. The distance dx in Fizeau’s experiment was equal to the length of light’s round-trip path length.
𝑑𝑥 = 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒𝑠 𝑡𝑟𝑎𝑣𝑒𝑙𝑒𝑑 𝑖𝑛 𝑓𝑟𝑎𝑚𝑒 𝑆
𝑑𝑡 = 𝑡𝑖𝑚𝑒𝑠 𝑚𝑒𝑎𝑠𝑢𝑟𝑒𝑑 𝑖𝑛 𝑓𝑟𝑎𝑚𝑒 𝑆
Okay, let’s get into the model.
If light is absorbed by the molecules of the refractive medium, it will travel at speed w while absorbed.
Now, scientists who were awarded the 2023 Nobel Prize for physics demonstrated that there are attosecond delays when photons are absorbed and then subsequently re-emitted by atoms or molecules, which is consistent with the model shown here.
But when traveling between molecules the light will travel at another speed influenced by the properties of the refractive medium. While absorbed or retained by a molecule, if the refractive medium is stationary, that is if w equals zero, light remains stationary while clocks continue to tick. But when light is re-emitted or no longer impeded by the molecules, it travels at a speed influenced by the environment of the refractive medium.
This will cause light to appear to move slower, overall, through a stationary medium, due in part to the time spent absorbed or impeded by stationary molecules. Here, n can be thought of as a resistance factor governing the overall rate at which light can navigate the fields and molecules of the refractive medium.
Now what happens when the water molecules move with respect to Frame S?
Whether absorbed or impeded by water molecules, light will travel at plus or minus w meters per second depending on the direction of the light signal with respect to the velocity of water through Frame S.
\(𝑢_{\text{𝑎𝑏𝑠𝑜𝑟𝑏𝑒𝑑 𝑜𝑟 𝑖𝑚𝑝𝑒𝑑𝑒𝑑 𝑏𝑦 𝑚𝑜𝑣𝑖𝑛𝑔 𝑤𝑎𝑡𝑒𝑟 𝑚𝑜𝑙𝑒𝑐𝑢𝑙𝑒}} \) = ± 𝑤 𝑚𝑒𝑡𝑒𝑟𝑠/𝑠𝑒𝑐𝑜𝑛𝑑
But when light travels between water molecules something unexpected happens. I am going to propose that the emitting water molecules impart their velocity, w, to the light signal, and that this is added to the speed at which light travels between water molecules.

Picture a bullet being fired from the front of a fast-moving vehicle versus from a stationary vehicle. The bullet being fired from the fast-moving vehicle will travel faster than the other bullet.
Look, I know that this is the opposite of what you’ve been taught about light, but bear with me because you are going to be amazed as we continue to develop this unconventional model.
Another thing that might not be immediately obvious is that light will travel a longer distance between molecules that are moving in the same direction as the light signal, and a shorter distance between molecules that are moving opposite to the direction of the light signal.
The relative motion of the water molecules will alter the distance traveled between them, and that will increase the time required for light to travel the total length of the water column, a distance we call dx in Frame S.
Now, I’m going to propose that these phenomena produce a compound light speed in Frame S governed by the following formula: c times dt divided by n times dt plus or minus w over c times dt all plus or minus w.
Let’s see if we can develop an intuitive sense for this formula.
𝑢 = \(\frac{𝑐𝑑𝑡}{𝑛𝑑𝑡 ± \frac{𝑤}{𝑐}𝑑𝑡} \) ± 𝑤
The numerator represents the distance that light will travel through Frame S in vacuum in dt stationary Frame seconds.
𝑢 = \(\frac{𝑐𝑑𝑡}{𝑛𝑑𝑡 ± \frac{𝑤}{𝑐}𝑑𝑡} \) ± 𝑤
As for the denominator, the first component is n times dt.
𝑢 = \(\frac{𝑐𝑑𝑡}{𝑛𝑑𝑡 ± \frac{𝑤}{𝑐}𝑑𝑡} \) ± 𝑤
This is the amount of time required for light to travel the distance computed by the numerator, but now while passing through a refractive medium instead of through vacuum. For water, n is 1.333. So, it takes 1.333 times longer for light to travel through a length of stationary water as compared to the same length of space.
The second term in the denominator is w over c times dt.
𝑢 = \(\frac{𝑐𝑑𝑡}{𝑛𝑑𝑡±\frac{𝑤}{𝑐}𝑑𝑡} \) ± 𝑤
When water molecules move in the same direction as light, it takes more time for light to spring from one water molecule and reach another water molecule, or to simply complete the journey through the entire column of water, because the leading edge of the water column moves away from the oncoming light signal. And this extra time is in proportion to the speed of the water, w, divided by the total speed of light through vacuum, c.
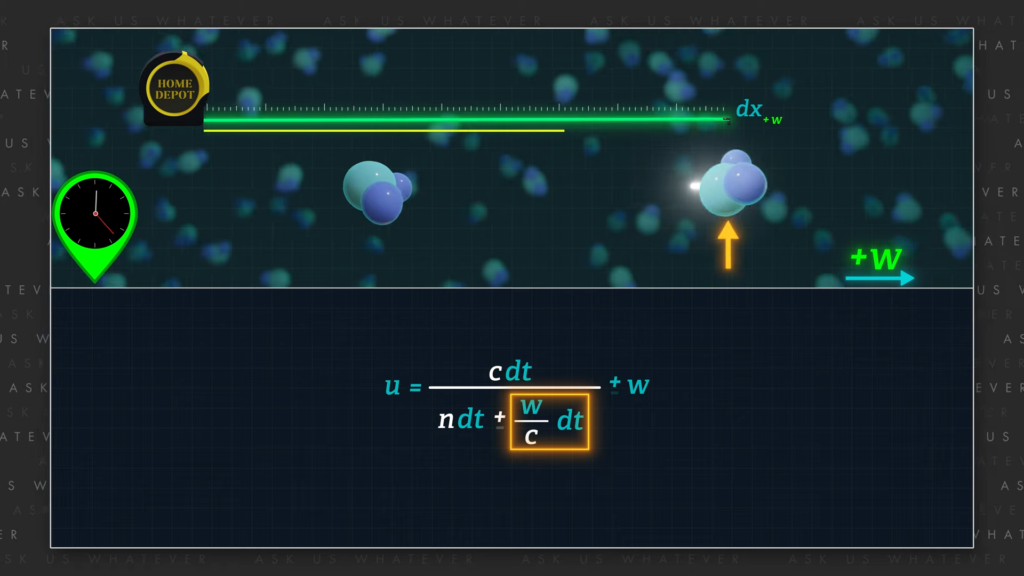
We thus find that the denominator is the total time required for light to pass through an array of moving water molecules.
𝑢 = \(\frac{𝑐𝑑𝑡}{𝑛𝑑𝑡 ± \frac{𝑤}{𝑐}𝑑𝑡} \) ± 𝑤
When water molecules move against the direction of the light signal, it takes less time for light to reach the trailing edge of the water column, because the molecules move toward the light signal, and so we subtract w over c times dt from n times dt.
𝑢 = \(\frac{𝑐𝑑𝑡}{𝑛𝑑𝑡−\frac{𝑤}{𝑐}𝑑𝑡} \) − 𝑤
Finally, the second term of our general formula for u is plus or minus w.
𝑢 = \(\frac{𝑐𝑑𝑡}{𝑛𝑑𝑡±\frac{𝑤}{𝑐}𝑑𝑡} \) ± 𝑤
This is the differential speed of the light signal resulting from its being emitted by a moving source.
This is the analog to the incremental bullet speed imparted by a moving gun.
Now since the first term of these formulas for speed u contain dt in both the numerator and denominator, we can cancel the «dt»’s and write the general formula as, c divided by n plus or minus w over c, plus or minus w.
𝑢 = \(\frac{𝑐}{𝑛 ± \frac{𝑤}{𝑐}} \) ± 𝑤
OK, before we begin to discuss the implications of this formula, let’s do a couple of reality checks.
Let’s first expand the formula using a Taylor series expansion.
𝑢 = \(\frac{𝑐}{𝑛±\frac{𝑤}{𝑐}} ± 𝑤 = \frac{\frac{𝑐}{𝑛}}{1±\frac{𝑤}{𝑛𝑐}} ± 𝑤 ≈ \frac{𝑐}{𝑛}( 1 ∓ \frac{𝑤}{𝑛𝑐} ± \frac{𝑤^2}{𝑛^2𝑐^2} −…) ± 𝑤 ≈ \)
\(\frac{𝑐}{𝑛} ∓ \frac{𝑤}{𝑛^2} ± 𝑤 = 𝑐/𝑛 ± 𝑤(1 − \frac{1}{𝑛^2}) \)
We can see that the formula I’ve proposed expands to the Fresnel/Fizeau formula for light speed through refractive media. This is not proof that my formula is correct, but von Laue offered no more “proof” than this to declare that Special Relativity explained the Fizeau result.
Let’s also plug some numbers into my formula to see if it predicts the fringe shift observed by Fizeau. We can first compute the difference in travel time by simply taking the ratio of dx (a fixed path length in Fizeau’s setup) divided by my formula’s values for u.
\(𝑑𝑡_\text{𝑢𝑝𝑠𝑡𝑟𝑒𝑎𝑚} − 𝑑𝑡_\text{𝑑𝑜𝑤𝑛𝑠𝑡𝑟𝑒𝑎𝑚} = \frac{𝑑𝑥}{𝑢_\text{𝑢𝑝𝑠𝑡𝑟𝑒𝑎𝑚}} − \frac{𝑑𝑥}{𝑢_\text{𝑑𝑜𝑤𝑛𝑠𝑡𝑟𝑒𝑎𝑚}} \)
The fringe shift expected at the location where upstream and downstream light signals reunite can be computed by multiplying this difference in travel times by the frequency of the light.
𝑓𝑟𝑖𝑛𝑔𝑒 𝑠ℎ𝑖𝑓𝑡 = \(𝜈(\frac{𝑑𝑥}{𝑢_\text{𝑢𝑝𝑠𝑡𝑟𝑒𝑎𝑚}} − \frac{𝑑𝑥}{𝑢_\text{𝑑𝑜𝑤𝑛𝑠𝑡𝑟𝑒𝑎𝑚}}) \)
And if we substitute the actual values used in Fizeau’s experiment, we obtain a predicted fringe shift of about 0.208 fringes.
𝑑𝑥 = 2.974 𝑚𝑒𝑡𝑒𝑟𝑠
𝑤 = 7.095 𝑚𝑒𝑡𝑒𝑟𝑠 𝑝𝑒𝑟 𝑠𝑒𝑐𝑜𝑛𝑑
𝑛 = 1.333
𝑙𝑖𝑔ℎ𝑡 𝑤𝑎𝑣𝑒𝑙𝑒𝑛𝑔𝑡ℎ = 526 𝑛𝑎𝑛𝑜𝑚𝑒𝑡𝑒𝑟𝑠
𝑙𝑖𝑔ℎ𝑡 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 = 5.699 𝑥 \(10^{14} \) 𝑤𝑎𝑣𝑒𝑠 𝑝𝑒𝑟 𝑠𝑒𝑐𝑜𝑛𝑑
0.207910340627825 𝑓𝑟𝑖𝑛𝑔𝑒𝑠 𝑝𝑟𝑒𝑑𝑖𝑐𝑡𝑒𝑑
The exact computation turns out to be identical to the fringe shift predicted by von Laue’s formula out to at least 15 significant digits. So, we’ve arrived at the same result without involving Special Relativity. That’s huge! We used Galilean relativity and Newtonian principles to build a plausible, physical model for how light moves through a refractive medium, and obtained the same answer as von Laue at non-relativistic water speeds.
So how do our predictions compare to Fizeau’s actual data? He reported observing a fringe shift of about 0.23 fringes, which puts us (or him) in the ballpark. But the point is that one can hardly differentiate von Laue’s Special Relativity model and my non-relativistic model based on that one data point.
Okay, you skeptical Einsteinians might still think I’m full of ether, so I’m now going to show you something absolutely fascinating.

Let’s rearrange von Laue’s relativistic velocity addition formula using some simple algebra.
𝑢 = \(\frac{\frac{𝑐}{𝑛} + 𝑤}{1 + \frac{𝑤}{𝑐𝑛}} = \frac{𝑐^2 + 𝑤𝑐𝑛}{𝑐𝑛 + 𝑤} = \frac{𝑐^2 − 𝑤^2 + 𝑤𝑐𝑛 + 𝑤^2}{𝑐𝑛 + 𝑤} \)
𝑢 = \(\frac{𝑐^2−𝑤^2 + 𝑤𝑐𝑛 + 𝑤^2}{𝑐𝑛+𝑤} = \frac{𝑐^2−𝑤2}{𝑐∗(𝑛+\frac{𝑤}{𝑐})} + 𝑤 = \frac{\frac{𝑐}{𝛾^2_𝐿}}{𝑛±\frac{𝑤}{𝑐}} ± 𝑤 \)
Well, would you look at that!
Von Laue’s formula for velocity addition in a refractive medium can be rearranged, using basic algebra, to my formula if we just insert a gamma squared term beneath the c term in the numerator.
Yes, my Einsteinian friends, it appears that my non-relativistic model for light moving through a refractive medium might be the underlying basis for the Fresnel/Fizeau phenomenon,
and for von Laue’s formula, minus the length contraction and time dilation adjustments that make no difference to the computational result at slow water speeds.
OK, but I’m sure you’re thinking that at relativistic speeds there will be a computational difference.
So, let’s explore the meaning of the gamma-squared terms in von Laue’s formula. The c in the numerator in von Laue’s formula represents light speed as measured from within the frame of the moving water. In other words, measured using the tools of Frame S’. Such a speed will be denominated in Frame S’ meters’ per second’
So to compute the speed of light, u, in Frame S, which is our goal, we must convert the Frame S’ speed of light to its equivalent speed in stationary Frame S. Special Relativity claims that observers in Frame S will be using longer meter sticks and faster clocks than observers in Frame S’.
𝑐′ 𝑐𝑜𝑛𝑣𝑒𝑟𝑡𝑒𝑑 𝑡𝑜 𝑓𝑟𝑎𝑚𝑒 𝑆 𝑚𝑒𝑎𝑠𝑢𝑟𝑖𝑛𝑔 𝑡𝑜𝑜𝑙𝑠 = \(\frac{𝑑𝑥}{𝑑𝑡} = 𝑐′\frac{𝑚𝑒𝑡𝑒𝑟𝑠′}{𝑠𝑒𝑐𝑜𝑛𝑑′} ∗ \frac{1}{𝛾𝐿} \frac{𝑠𝑒𝑐𝑜𝑛𝑑′}{𝑠𝑒𝑐𝑜𝑛𝑑} ∗ \frac{1}{𝛾𝐿} \frac{𝑚𝑒𝑡𝑒𝑟}{𝑚𝑒𝑡𝑒𝑟′} = 𝑐′/𝛾^2_𝐿 𝑚𝑒𝑡𝑒𝑟𝑠/𝑠𝑒𝑐𝑜𝑛𝑑 \)
And so, speed c prime, that is, the speed of light as measured in Frame S’ and as denominated in units of meters’ per second’, must be divided by the Lorentz gamma factor squared to find its equivalent value in Frame S as denominated in units of meters per second.
And so, if we want to take my non-relativistic model and conform it to Special Relativity, we merely need to divide the speed of light as measured in Frame S’ (the c in the numerator) by the Lorentz gamma-factor-squared.
𝑢 = \(\frac{\frac{𝑐}{𝛾^2_𝐿}}{𝑛±𝑤𝑐} ±𝑤 \)
Note that the c in the denominator does not need to be converted because it already represents a Frame S speed as measured in Frame S meters per second.
And of course, we can take the algebra in the reverse direction to show that the Special Relativity version of my formula equals von Laue’s formula for light speed through a refractive medium moving at speed w.
𝑢 = \(\frac{\frac{𝑐}{𝛾^2_𝐿}}{𝑛 ±\frac{𝑤}{𝑐}} ± 𝑤 = \frac{𝑐^2−𝑤^2}{𝑐∗(𝑛+\frac{𝑤}{𝑐})} + 𝑤 = \frac{𝑐^2−𝑤^2+𝑤𝑐𝑛+𝑤^2}{𝑐𝑛+𝑤} = \)
\(= (𝑐^2 − 𝑤^2 + 𝑤𝑐𝑛 + 𝑤^2)/(𝑐𝑛+𝑤) = (𝑐^2 + 𝑤𝑐𝑛)/(𝑐𝑛+𝑤) = \frac{\frac{𝑐}{𝑛} + 𝑤}{1 + \frac{𝑤}{𝑐𝑛}} \)
When we plug experimental parameters into this re-stated form of my formula, we of course get exactly the same fringe shift as predicted by von Laue, at any water speed.
Unfortunately, von Laue’s and Einstein’s velocity addition formula gives no insight into the molecular mechanism for the speed of light through a refractive medium.
Their formula suggests that light speed relative to moving water
𝑢 = \(\frac{𝑐/𝑛+𝑤}{1+\frac{(\frac{𝑐}{𝑛})𝑤}{𝑐^2}} = \frac{𝑐/𝑛}{1+\frac{(\frac{𝑐}{𝑛})𝑤}{𝑐2}} + \frac{𝑤}{1+\frac{(\frac{𝑐}{𝑛})𝑤}{𝑐^2}} \)
and water speed relative to the laboratory
𝑢 = \(\frac{𝑐/𝑛+𝑤}{1+\frac{(\frac{𝑐}{𝑛})𝑤}{𝑐2}} = \frac{𝑐/𝑛}{1+\frac{(\frac{𝑐}{𝑛})𝑤}{𝑐2}} + \frac{𝑤}{1+\frac{(\frac{𝑐}{𝑛})𝑤}{𝑐^2}} \)
are both somehow slowed by a mystical relativistic factor in the denominator.
𝑢 = \(\frac{𝑐/𝑛+𝑤}{1+\frac{(\frac{𝑐}{𝑛})𝑤}{𝑐^2}} = \frac{𝑐/𝑛}{1+\frac{(\frac{𝑐}{𝑛})𝑤}{𝑐^2}} + \frac{𝑤}{1+\frac{(\frac{𝑐}{𝑛})𝑤}{𝑐^2}} \)
What is the physical meaning of von Laue’s second term?
𝑢 = \(\frac{𝑐/𝑛+𝑤}{1+\frac{(\frac{𝑐}{𝑛})𝑤}{𝑐2}} = \frac{𝑐/𝑛}{1+\frac{(\frac{𝑐}{𝑛})𝑤}{𝑐2}} + \frac{𝑤}{1+\frac{(\frac{𝑐}{𝑛})𝑤}{𝑐2}} \)
Is it implying that the speed of the water, w, is being slowed by some magical relativistic force of the universe? Obviously, it cannot be, since w is the speed of Frame S’, which in the case of the Fizeau experiment is the water speed of the experimental setup.
Von Laue’s second term is not grounded in reality. It’s just part of the formula salad that makes up Special Relativity.
My formula, on the other hand, conforms to an explanation grounded in the physical world. So, let’s explore the implications of the non-relativistic version of my formula.
𝑢 = \(\frac{𝑐}{𝑛±\frac{𝑤}{𝑐}}±𝑤 \)
I’m going to use some artistic license here and call the first term the “refractive speed”.
\(𝑢_𝑟 = \frac{𝑐}{𝑛±\frac{𝑤}{𝑐}} \)
Using the analogy of a gun being fired from a moving vehicle, this is the speed of the bullet if it had been fired from a gun that is stationary in Frame S relative to the speed of the vehicle.
Speed w is the speed of the vehicle as measured in Frame S.
𝑢 = \(\frac{𝑐}{𝑛±\frac{𝑤}{𝑐}} ± 𝑤 \)
If a gun is fired while a vehicle is moving at speed w, the vehicle speed, or essentially the emitter speed, will be linearly added to the native speed of the bullet. I’m going to call speed w the “ballistic speed”.
\(𝑢_𝑏 \) = ± 𝑤
Now, it’s important to appreciate that the ballistic speed is a component of light speed, not only when associated with water molecules, but ALL OF THE TIME. Whether absorbed by a water molecule or traveling freely between water molecules, the ballistic speed is a component of total light speed.
\(𝑢_𝑟 = \frac{𝑐}{𝑛±\frac{𝑤}{𝑐}} \) \(𝑢_𝑏 \) = ± 𝑤
𝑢 = \(\frac{𝑑𝑥}{𝑑𝑡} \) 𝑢 = \(𝑢_𝑟 + 𝑢_𝑏 = \frac{𝑐}{𝑛±\frac{𝑤}{𝑐}} ± 𝑤 \)
You may think that this concept violates Einstein’s second postulate of Special Relativity; but if we read that postulate carefully, …
Any ray of light moves in the “stationary” system of co-ordinates with the determined velocity c, whether the ray be emitted by a stationary or by a moving body.
…it merely says that the total speed of light will be constant “whether emitted by a stationary or by a moving body”. Therefore, Special Relativity does not rule out the possibility that the emitting body contributes to total light speed, provided that total light speed in vacuum sums to speed c.
So how did Einstein pull off that cute trick?
The gamma squared term in the numerator of von Laue’s re-arranged formula is what forces Einstein’s formula for total light speed to be constant in vacuum.
𝑢 = \(\frac{𝑐/𝛾^2_𝐿}{𝑛±\frac{𝑤}{𝑐}} ± 𝑤 = \frac{𝑐/𝛾^2_𝐿}{1±\frac{𝑤}{𝑐}} ± 𝑤 = \frac{(𝑐+𝑤)(𝑐−𝑤)}{𝑐±𝑤} ± 𝑤 = 𝑐 \)
And as I explained earlier, the gamma-squared term originates from the concepts of differential time dilation and length contraction between our two reference Frames S and S’.
And because of the gamma-squared term, which Special Relativity requires based on its fundamental principles, we must also include plus or minus w in the formula, otherwise the formula will not add up to speed c.
𝑢 = \(\frac{𝑐/𝛾^2_𝐿}{𝑛±\frac{𝑤}{𝑐}} ± 𝑤 = \frac{𝑐/𝛾^2_𝐿}{1±\frac{𝑤}{𝑐}} ± 𝑤 = \frac{(𝑐+𝑤)(𝑐−𝑤)}{𝑐±𝑤} ± 𝑤 = 𝑐 \)
In other words, when light moves through vacuum, such that n equals 1, light speed still comprises a component speed, w, which must be attributable to something moving at speed w. Well, if there is only vacuum and no refractive medium, then there are no molecules or molecular fields to “drag” light in the direction of moving Frame S’.
So, then what does w represent in vacuum? It’s the speed of the emitter and the receiver moving along with Frame S’. When light is emitted from a source, it takes with it a component of speed equal to the speed of the source. In our gun analogy, the moving vehicle and thus the moving gun contribute the speed of the vehicle and the gun to the speed of the bullet. I cannot over-emphasize this point: the source contributes its velocity to the light signal, and such velocity is maintained as a component of light speed irrespective of the presence or absence of a refractive medium.
Do you know what this means? It means that a component of light speed must comprise the speed imparted by the emitter, what I call the ballistic speed.
Even though Einstein engineered his light speed formulas to add up to speed c, by invoking length contraction and time dilation, the speed of the emitter is hidden within them.
I believe this to have significant implications for the momentum of light and possibly for the argument that light might have something like a mass. Yes, the concept that light has dual properties, both particle and wave, isn’t dead.
Please know that I am not advocating Walter Ritz’s 1908 emission theory here. Ritz proposed that total light speed is the linear sum of speed c plus or minus the speed of the emitter. That theory is not supported by experimental evidence.
Whereas, as I showed earlier, my model fully supports the Fizeau result and some new experimental data that I’ll introduce in the next episode.
There is another implication for von Laue’s Special Relativity formula for light speed. If you believe in Special Relativity, you must believe that length contraction is a real, physical event that actually changes the lengths of measuring tools. Length contraction cannot be an ephemeral concept caused by the relativity of simultaneity, as so many textbooks falsely claim. That’s a gross misunderstanding of Special Relativity.
In order for Einstein’s velocity addition formula to yield a constant light speed of c, the gamma squared term must be included, and therefore length contraction must be a real, physical event. And as you know, I think the concept of length contraction is absurd and unworkable, and therefore Special Relativity is also deeply flawed.
Which is why I’m now going to claim that both von Laue’s formula and my non-relativistic formula are incorrect. Neither is perfect. We need to modify them using one more concept that comes from my alternative model of relativity to reach a better formula.
And in order to make my velocity addition formula relativistic, we need to address time dilation. Now you know, I don’t believe in length contraction, but I do believe that some types of clocks are impacted by their speed through the universe, particularly our gold-standard atomic clocks. And so, we need to look at which terms in the non-relativistic formula for speed u might be impacted by clock rate.
𝑢(𝑛𝑜𝑛−𝑟𝑒𝑙𝑎𝑡𝑖𝑣𝑖𝑠𝑡𝑖𝑐) = \(\frac{𝑑𝑥}{𝑑𝑡} = 𝑢_𝑟 + 𝑢_𝑏 = \frac{𝑐}{𝑛±\frac{𝑤}{𝑐}} ± 𝑤 \)
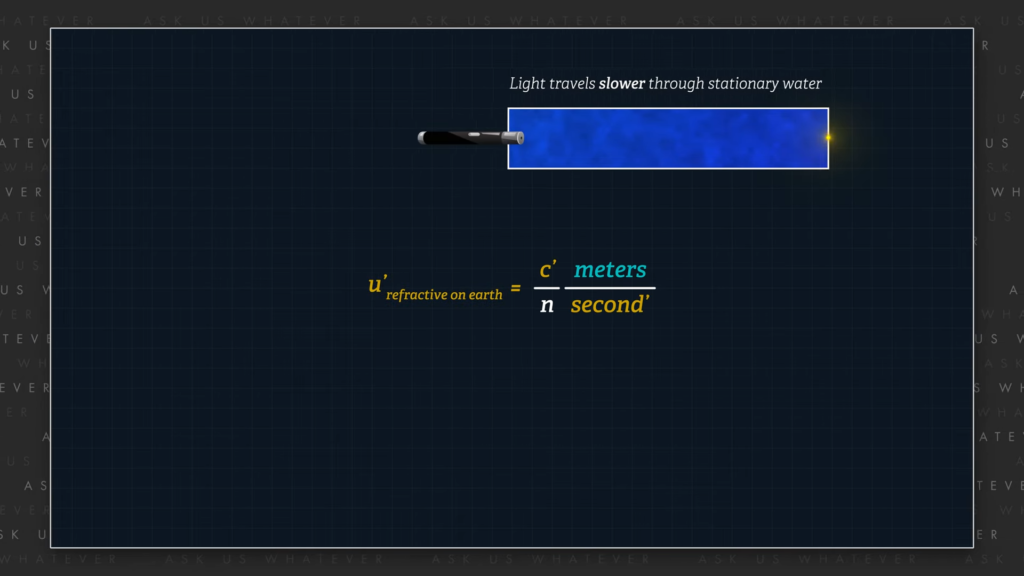
We’ll again start with the assumption that the speed of light passing through a refractive medium on Earth is c’ divided by n meters per second’. Note that I use normal meters here since there is no length contraction in the alternative model.
\(𝑢′_\text{𝑟𝑒𝑓𝑟𝑎𝑐𝑡𝑖𝑣𝑒 𝑜𝑛 𝐸𝑎𝑟𝑡ℎ} = \frac{𝑐′}{𝑛}\frac{𝑚𝑒𝑡𝑒𝑟𝑠}{𝑠𝑒𝑐𝑜𝑛𝑑′} \)
If we convert this to universal frame meters per second, we have c’ divided by gamma-s, to account for clock dilation, all divided by n.
\(𝑐/𝑛_\text{𝑖𝑛 𝑓𝑟𝑎𝑚𝑒 𝑆 𝑢𝑛𝑖𝑡𝑠} = \frac{𝑐′}{𝑛}\frac{𝑚𝑒𝑡𝑒𝑟𝑠}{𝑠𝑒𝑐𝑜𝑛𝑑′} ∗ \frac{1}{𝛾_𝑠}\frac{𝑠𝑒𝑐𝑜𝑛𝑑𝑠′}{𝑠𝑒𝑐𝑜𝑛𝑑} = \frac{𝑐′/𝛾_𝑠}{𝑛}\frac{𝑚𝑒𝑡𝑒𝑟𝑠}{𝑠𝑒𝑐𝑜𝑛𝑑} \)
\(𝑢′_\text{𝑖𝑛 𝑓𝑟𝑎𝑚𝑒 𝑆 𝑢𝑛𝑖𝑡𝑠} = \frac{𝑐′}{𝑛}\frac{𝑚𝑒𝑡𝑒𝑟𝑠}{𝑠𝑒𝑐𝑜𝑛𝑑′} ∗ \frac{1}{𝛾_𝑠}\frac{𝑠𝑒𝑐𝑜𝑛𝑑𝑠′}{𝑠𝑒𝑐𝑜𝑛𝑑} = \frac{𝑐′/𝛾_𝑠}{𝑛}\frac{𝑚𝑒𝑡𝑒𝑟𝑠}{𝑠𝑒𝑐𝑜𝑛𝑑} \)
Let’s now use the same logic for adding water speed linearly and modulating inter-molecular light speed by the differential distance effect.
𝑢 = \(\frac{\frac{𝑐′}{𝛾_𝑠}}{𝑛+\frac{𝑤}{𝛾_𝑠𝑐}} + 𝑤 \)
Here we use the ratio of water speed in meters per second divided by gamma-s times c meters per second, which as you know from the alternative model covered in Episodes 6.1 and 6.2 is light speed as emitted by a source moving through space, where, gamma-s is computed using the speed of the emitting source through space, w meters per second.
\(𝛾_𝑠 = \sqrt{1+\frac{𝑤^2}{𝑐^2}} \)
Interestingly, this formula is independent of clock offset, which makes it completely compatible with the Fizeau experiment in which there were no clocks.
𝑢 = \(\frac{\frac{𝑐′}{𝛾_𝑠}}{𝑛±\frac{𝑤}{𝛾_𝑠𝑐}} ± 𝑤 \)
The removal of Einstein clock synchronization changes some of the fundamental transformation formulas, which I’ll show here for completeness, but not call out.
This leads to the fascinating result that the one-way speed of light in a refractive medium, when measured with absolutely synchronized clocks, is, c-prime divided by n plus or minus w over gamma(s) times c.
\(𝑢′_\text{𝑎𝑙𝑡𝑒𝑟𝑛𝑡𝑖𝑣𝑒} = \frac{𝑑𝑥′}{𝑑𝑡′} = \frac{𝑐′}{𝑛±\frac{𝑤}{𝛾_𝑠𝑐}} \)
We can then see a resemblance to the formula for dx/dt.
\(𝑢_\text{𝑎𝑙𝑡𝑒𝑟𝑛𝑡𝑖𝑣𝑒} = \frac{𝑑𝑥}{𝑑𝑡} = \frac{𝑐′/𝛾_𝑠}{𝑛±\frac{𝑤}{𝛾_𝑠𝑐}} ± 𝑤 \)
Other than the gamma(s) term in the numerator, which is there to compensate for the effect of time dilation on clock rate, the one-way speed of light in the stationary frame is essentially the one-way speed of light in the moving frame, plus or minus the ballistic speed w of the emitter.
Let me repeat, when absolutely synchronized clocks are used instead of Einstein-synchronized clocks, we reveal that the speed at which Frame S’ moves through Frame S, speed w, is added to the speed at which light moves through Frame S’ as adjusted for the effects of time dilation on clock rates. Please note that both speeds are modulated by the w divided by gamma(s) times c term, which essentially prolongs or reduces travel time by changing light’s travel distance.
With these formulas, we can now predict the impact of refractive media speed on fringe shift.
The formula for fringe shift is the same but with the alternative values of speeds u upstream and downstream.
𝑓𝑟𝑖𝑛𝑔𝑒 𝑠ℎ𝑖𝑓𝑡 = \(𝜈(\frac{𝑑𝑥}{𝑢_\text{𝑢𝑝𝑠𝑡𝑟𝑒𝑎𝑚}}−\frac{𝑑𝑥}{𝑢_\text{𝑑𝑜𝑤𝑛𝑠𝑡𝑟𝑒𝑎𝑚}}) \)
When Fizeau’s actual experimental parameters are plugged into these alternative model equations, they also predict a fringe shift of 0.208 fringes. And so, the alternative model, coupled with this new analysis of the Fizeau experiment, is able to predict the same fringe shift as von Laue’s model without the complexity of an illusory length contraction, and without the confusion associated with non-existent clock synchronization.

The fact that all three models predict the same fringe shift is merely due to the extremely slow water speed used in Fizeau’s experiment.
It’s interesting to see what the alternative model predicts for Frame S vacuum light speed coming from a moving emitter in Frame S’. In vacuum, n equals 1.
\(𝑛_\text{𝑣𝑎𝑐𝑢𝑢𝑚} = 1 \)
𝑢 = \(\frac{\frac{𝑐}{𝛾_𝑠}}{1±\frac{𝑤}{𝛾_𝑠𝑐}} ± 𝑤 = \frac{\frac{𝑐}{𝛾_𝑠}±𝑤+\frac{𝑤^2}{𝛾_𝑠𝑐^2}}{1±\frac{𝑤}{𝛾_𝑠𝑐}} = \frac{𝑐(1±\frac{𝛾_𝑠𝑤}{𝑐}+\frac{𝑤^2}{𝑐^2})}{𝛾_𝑠±\frac{𝑤}{𝑐}} = \frac{𝑐(𝛾^2_𝑠±\frac{𝛾_𝑠𝑤}{𝑐})}{𝛾_𝑠±\frac{𝑤}{𝑐}} = 𝛾_𝑠𝑐\frac{𝛾_𝑠±\frac{𝑤}{𝑐}}{𝛾_𝑠±\frac{𝑤}{𝑐}} \)
\(𝑢_\text{𝑒𝑚𝑖𝑡𝑡𝑒𝑑 𝑓𝑟𝑜𝑚 𝑎 𝑚𝑜𝑣𝑖𝑛𝑔 𝑠𝑜𝑢𝑟𝑐𝑒} = 𝛾_𝑠𝑐 \) 𝑚𝑒𝑡𝑒𝑟𝑠/𝑠𝑒𝑐𝑜𝑛𝑑
And so light speed coming from a moving emitter as measured in Frame S is gamma-s times c when emitted either parallel or antiparallel to the direction of motion of Frame S’. This is exactly what is predicted by the alternative model covered in Episodes 6.1 and 6.2.
As is known in astronomy, light emitted from some binary stars arrives at the Earth at the same time, suggesting that it traveled to the Earth from the receding and the approaching stars at the same speed.
My model, unlike Ritz’s model, also predicts that light will travel at the same speed, whether emitted in the direction of emitter motion or opposite to the direction of emitter motion. And, most interestingly, my model predicts that light will travel at a speed that exceeds speed c when measured in the reference frame of the universe. That has enormous implications for cosmology, the apparent expansion of the universe, the Hubble theory, and the cosmic background radiation.

So, once again we have corrected some flaws in the Special Theory of Relativity, as well as the misguided thinking of some of its advocates, such as von Laue and the textbook authors who came after him.
Unfortunately, the rapid and broad acceptance of von Laue’s model has caused the real mechanism governing light speed through refractive media to be hidden for over a hundred years. I’m confident that if physicists would stop covering up for the flaws in Special Relativity, we will open the door to some significant new progress in the field of physics.
And physics journals that automatically reject papers critical of Special Relativity should be embarrassed for propagating a religion rather than pursuing pure science. I mean, I’m not going to name names, but Physical Review, and Nature, and The American Journal of Physics might be feeling their ears burning right about now. J
OK, that’s enough for now. If you have any questions, please write them in the comments section. I’m Joe Sorge, and thanks for watching.