Welcome to Ask Us Whatever! I’m Joe Sorge.
Let’s start out with what is meant by the principle of relativity. The principle was first attributed to Galileo Galilei, who in 1632 in his Dialog Concerning the Two Chief World Systems, used an example of a ship floating on a smooth sea at constant velocity.
He stated that an observer below deck would not be able to discern if the ship was moving. In other words, the laws that govern the motion of objects would operate the same regardless of the speed of the ship.
The principle was later broadened to: the equations describing the laws of physics must have the same form in all inertial frames of reference.
This implies that there is a symmetry to the laws of physics. A law of physics must look the same to one inertial observer as it does to another inertial observer.
Einstein and Lorentz took this further. They believed that one could use certain equations, or transforms, to predict certain quantities within an inertial system by knowing similar quantities in another inertial system moving at a known speed with respect to the first system.
Einstein stated, in his 1907 paper on Special Relativity:
“If one solves the ‘transformation’ equations with respect to x,y,z,t, one obtains the same equations, except that the “primed” quantities are replaced by the corresponding “unprimed” quantities, and conversely; and v is replaced by -v. This also follows directly from the principle of relativity…”
Einstein was saying that the transformation equations, which we often call the Lorentz transforms, are symmetric such that if an observer in a first inertial system believes that a second inertial system is moving at speed v, then an observer in the second inertial system will observe the first inertial system to be moving in the opposite direction at speed negative v; and that either observer can describe the motion of the other observer using a set of symmetrical equations.
But Einstein added an interesting paragraph to his 1905 relativity paper:
“If at the points A and B of K there are stationary clocks which, viewed in the stationary system, are synchronous; and if the clock at A is moved with the velocity v along the line AB to B, then on its arrival at B the two clocks no longer synchronize, but the clock moved from A to B lags behind the other which has remained at B by ½ t v^2/c^2…”
I’ve unpacked this statement in some of my other videos, but now let’s see what it means to the principle of relativity.
Einstein tells us that if the System K clocks are initially synchronized according to the method described in the first section of his 1905 paper, then a clock that moves with respect to that system will beat slower than a clock that remains stationary.
That’s why the reading on clock A will lag behind the reading on clock B when the clocks unite.
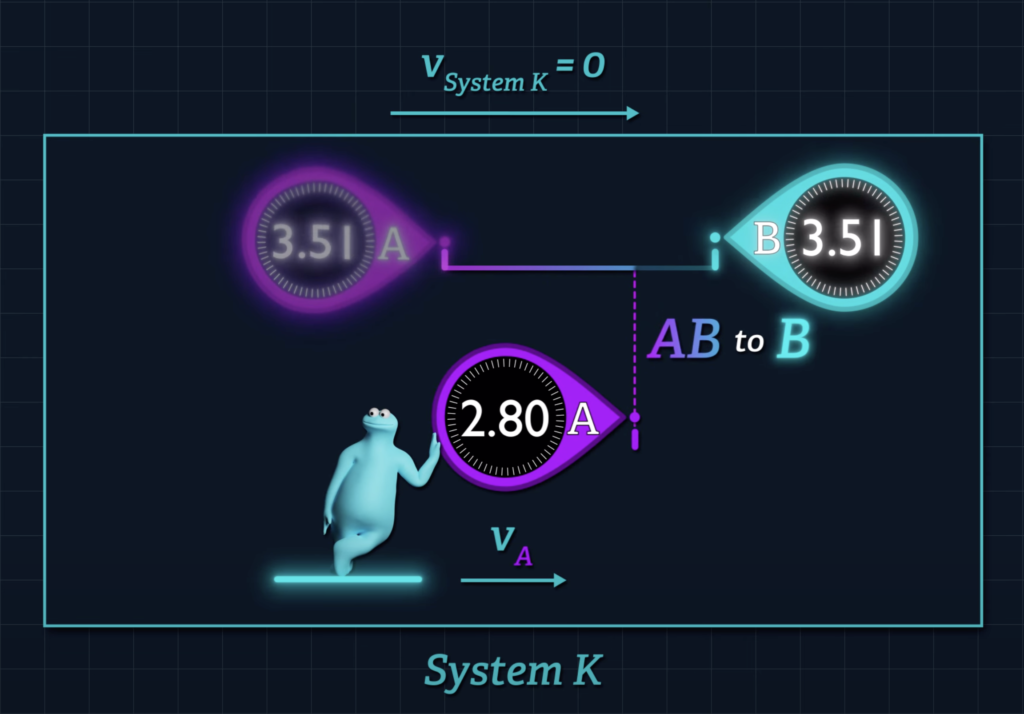
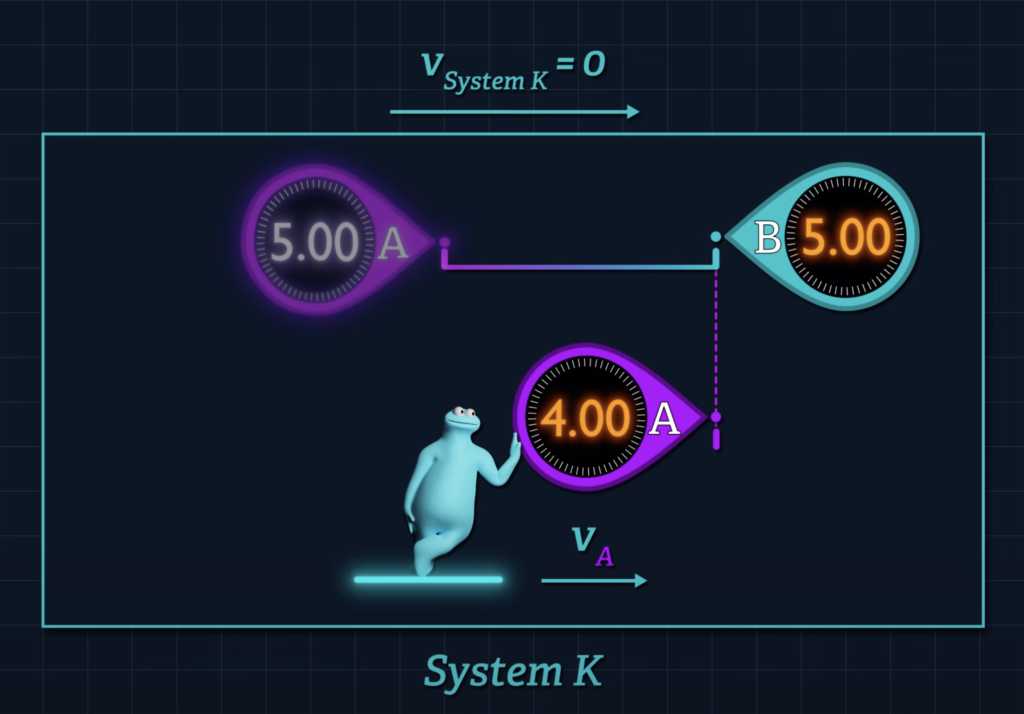
This effect is not some illusion related to the relativity of simultaneity. Einstein described a predictable and measurable difference in the readings of clocks A and B when they come together, a concept that has been supported with experimental evidence.
I’m going to show that System K does not need to be stationary in some absolute sense in order for his approximate formula to be true, provided that the clocks of System K were initially synchronized pursuant to Einstein’s protocol.
I am then going to describe an alternative experimental setup, using the principles of the 1905 paper, where the final difference in the readings on the clocks will depend on the speed, through space, of the system containing the clocks. In other words, observers in the system of the clocks will observe different outcomes depending on how fast their system travels with respect to some universal reference system.
This novel experiment will demonstrate that the principle of relativity is a fallacy, and that Special Relativity unknowingly proves that clock tempo and light speed are influenced by some universal, preferred system. If I succeed, it will be huge!
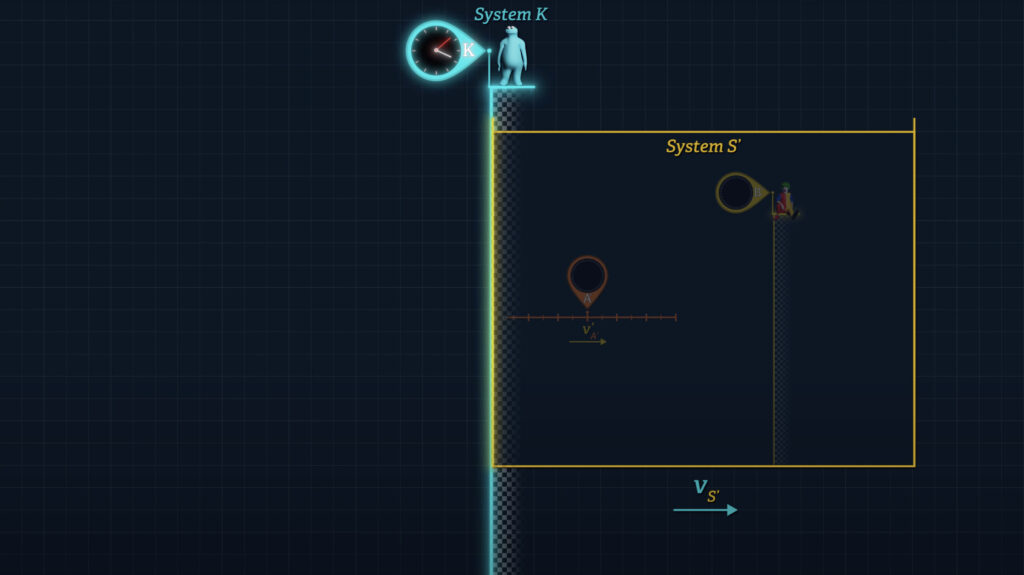
So, to illustrate the concepts, I’m going to generalize Einstein’s setup.
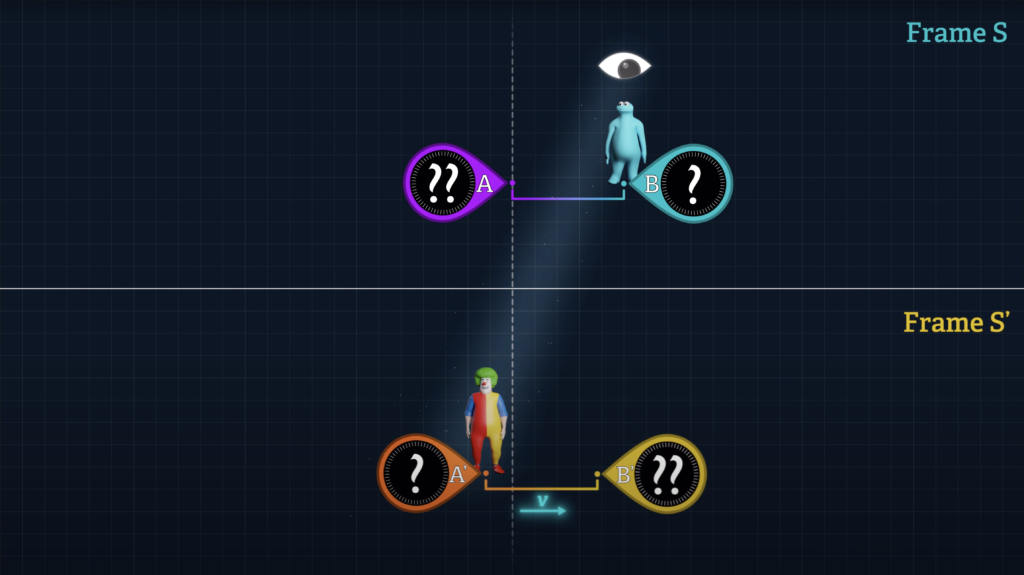
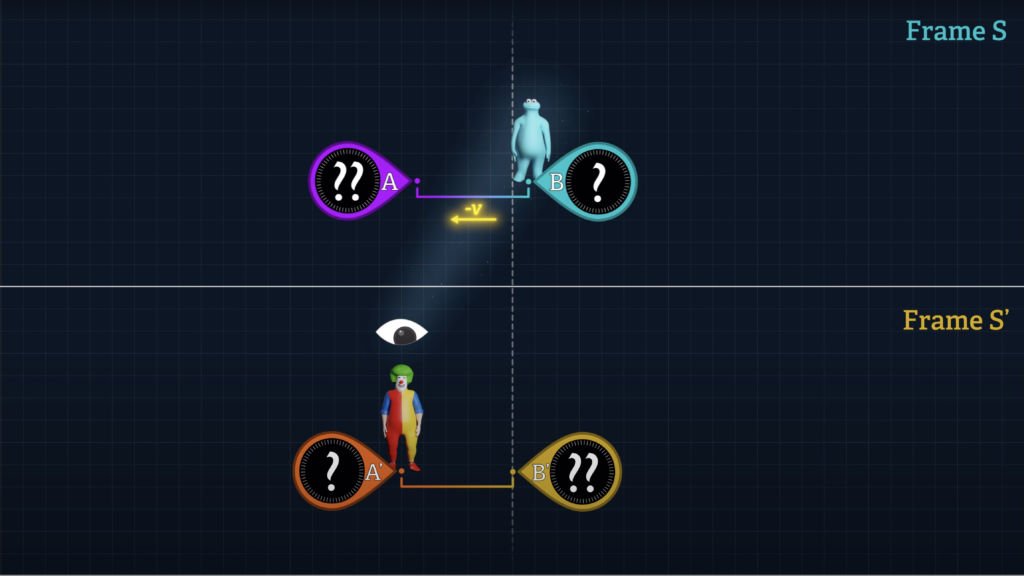
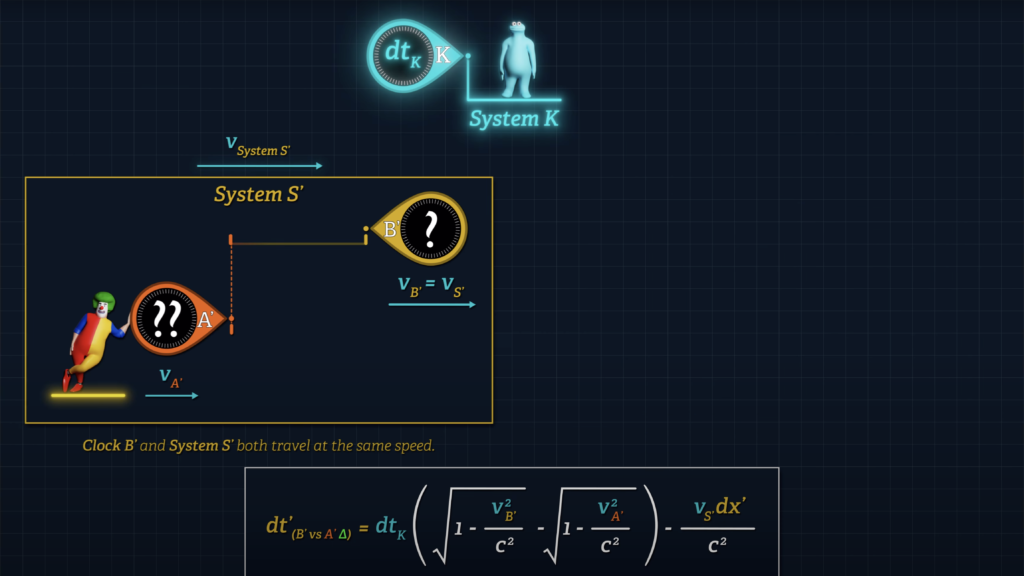
Let’s say that there is a System S’ that can be observed from System K. Let’s say that Clock B’ is stationary at the origin of System S’ and that Clock A’ moves over to Clock B’.
If we wish to quantify the difference in the readings displayed on Clocks A’ and B’ when they unite, we can do so with the following formula, where an observer in System K measures the speed of System S’, (labeled v-sub-S’), relative to System K, and the time dt-sub-K is the System K time for Clock A’ to travel to Clock B’.
\(d t^{\prime}{ }_{\left(\text {clocks } B^{\prime} v s \hspace{0.1cm} A^{\prime} \Delta\right)}=\color{#65a542} {d t_K}\left(\sqrt{1-\frac{v_{B^{\prime}}^2}{c^2}}-\sqrt{1-\frac{v_{A^{\prime}}^2}{c^2}}\right)-\frac{\color{#973b93}{v_{S^{\prime}}} d x^{\prime}}{c^2} \)
Only one System K clock is needed to measure the speed of Clock A’ – let’s call it Clock K. Note that elapsed time dt-sub-K is expressed in the time units of Clock K, in other words governed by the tempo of System K clocks.
Observers in System S’ can measure the initial proper distance separating the clocks, we’ll call it dx’, using System S’ measuring tools
Since Clock B’ is stationary in System S’, Clock B’ and System S’ both travel at the same speed, v-sub-S’ with respect to System K. And Clock A’ travels at speed v-sub-A’ with respect to System K.
\(d t^{\prime}{ }_{\left(\text {clocks } B^{\prime} v s \hspace{0.1cm} A^{\prime} \Delta\right)}=\color{#65a542}{d t_K}\left(\sqrt{1-\frac{v_{B^{\prime}}^2}{c^2}}-\sqrt{1-\frac{\color{#71b7eb}{v_{A^{\prime}}^2}}{c^2}}\right)-\frac{\color{#973b93}{v_{S^{\prime}}} \color{#dd7a42}{d x^{\prime}}}{c^2} \)
This formula accounts for the difference in tempo of Clocks A’ and B’ with respect to Clock K, and the right-most term accounts for the fact that Einstein deemed the clocks to be synchronous within the system of the clocks. I’ve included the Greek symbol delta in the subscript to dt’ to reflect initial Einstein clock synchronization.
\(d t^{\prime}{ }_{\left(\text {clocks } B^{\prime} v s \hspace{0.1cm} A^{\prime} \color{#ea3324}{\Delta}\right)}=d t_K\left(\color{#34749d}{\sqrt{1-\frac{v_{B^{\prime}}^2}{c^2}}-\sqrt{1-\frac{v_{A^{\prime}}^2}{c^2}}}\right)\color{#ea3324}{-\frac{v_{S^{\prime}} d x^{\prime}}{c^2}} \)
We covered Einstein clock synchronization extensively in Episode 7.2. In short, this procedure creates a difference in readings between Clocks A’ and B’, as observable from System K.
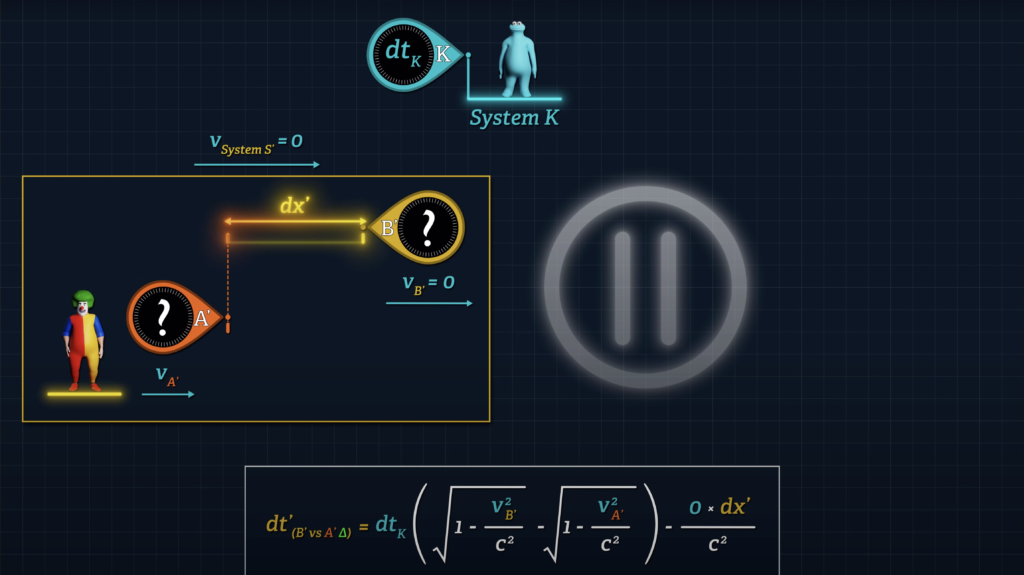
When System S’ is moving with respect to System K, the clock offset term is equal to the speed of System S’ with respect to System K, times dx’ over c squared.
\(\color{#ea3324}{-\frac{v_{S^{\prime}} d x^{\prime}}{c^2}} \)
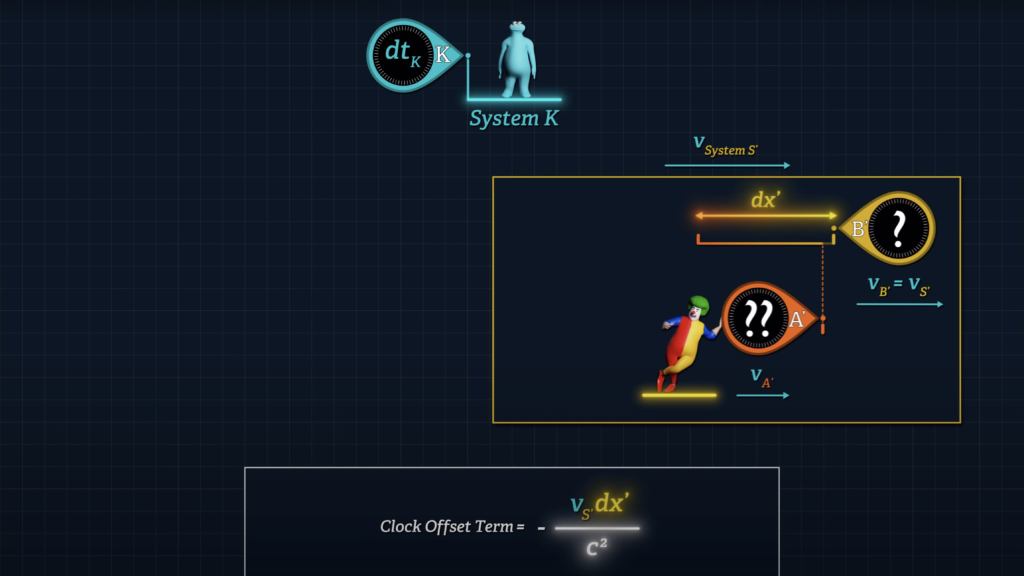
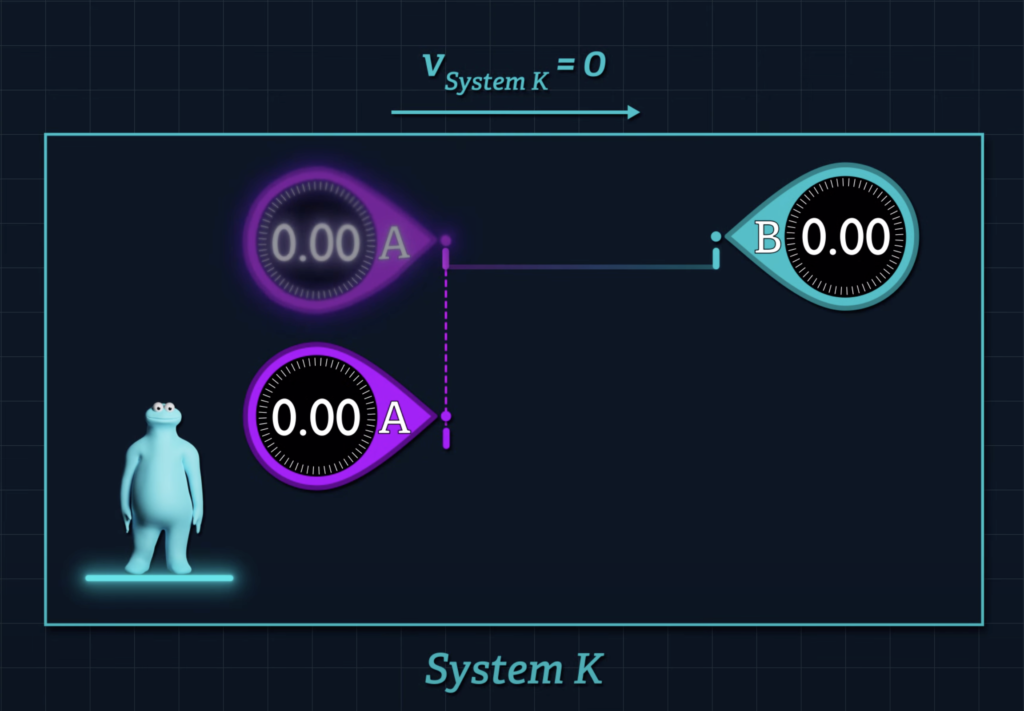
But when the speed of System S’ is zero, the v-sub-S’ term will be zero and Clocks A’ and B’ will report the same reading once synchronized, even though the two clocks are initially separated by distance dx’.
\(d t^{\prime}{ }_{\left(\text {clocks } B^{\prime} v s \hspace{0.1cm} A^{\prime} \color{#ea3324}{\Delta}\right)}=d t_K\left(\sqrt{1-\frac{v_{B^{\prime}}^2}{c^2}}-\sqrt{1-\frac{v_{A^{\prime}}^2}{c^2}}\right)-\frac{\color{#ea3324}{0 *} d x^{\prime}}{c^2} \)
In other episodes, I have referred to the difference in clock readings as a clock offset or as a spatial gradient of clock readings.
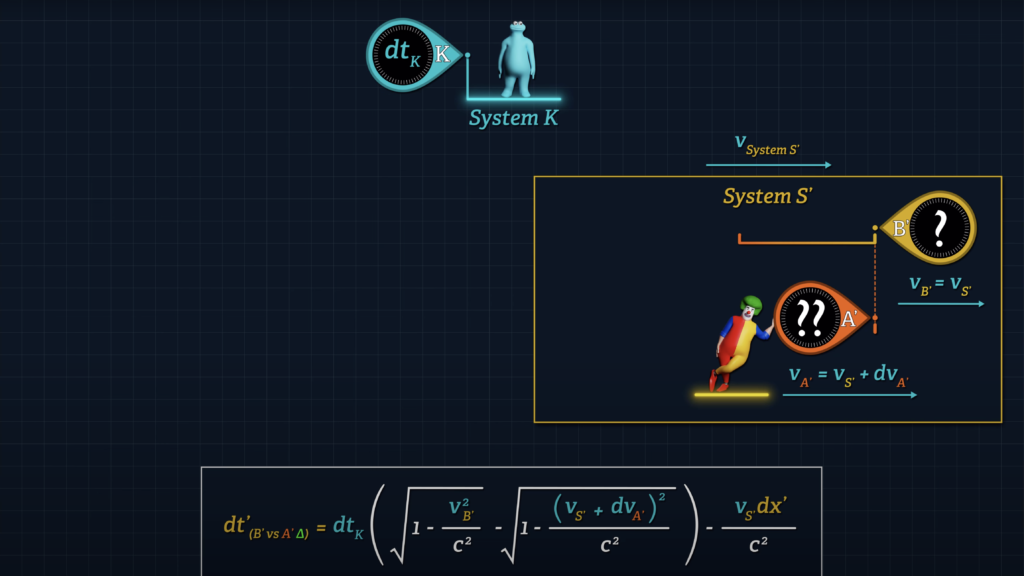
Since our Clock B’ is stationary in System S’, we can simplify our formula by replacing v-sub-B’ with the speed of System S’. We can then write speed v-sub-A’ as v-sub-S’ plus the incremental speed at which Clock A’ approaches Clock B’, as measured from System K in System K dimensional units. We will call that incremental speed dv-sub-A’.
\(d t^{\prime}{ }_{\left(\text {clocks } B^{\prime} v s \hspace{0.1cm} A^{\prime} \Delta\right)}=d t_K\left(\sqrt{1-\frac{v_{S^{\prime}}^2}{c^2}}-\sqrt{1-\frac{\left(v_{S^{\prime}}+\color{#ea3324}{d v_{A^{\prime}}}\right)^2}{c^2}}\right)-\frac{v_{S^{\prime}} d x^{\prime}}{c^2} \)
When the speed of System S’ is zero relative to System K, we can simplify our general formula to match Einstein’s example.
\(d t^{\prime}{ }_{\left(\text {clocks } B^{\prime} v s \hspace{0.1cm} A^{\prime}\right)}=d t_K\left(\sqrt{1-\frac{0^2}{c^2}}-\sqrt{1-\frac{\left(0+d v_{A^{\prime}}\right)^2}{c^2}}\right)-0 \)
\(d t^{\prime}{ }_{\left(\text {clocks } B^{\prime} v s \hspace{0.1cm} A^{\prime}\right)}=d t_K\left(1-\sqrt{1-\frac{\left(d v_{A^{\prime}}\right)^2}{c^2}}\right) \)
And if we use a Taylor series expansion to second order to approximate the square root term, we get, approximately one-half the time elapsed on Clock K, times the incremental speed of Clock A’ squared over c squared (when the speed of Clock A’ is very slow compared to speed c).
\(d t^{\prime}{ }_{\left(\text {clocks } B^{\prime} v s \hspace{0.1cm} A^{\prime}\right)}=d t_K\left(1-\sqrt{1-\frac{\left(d v_{A^{\prime}}\right)^2}{c^2}}\right) \approx d t_K\left(1-1+\frac{d v_{A^{\prime}}^2}{2 c^2}\right) \approx \frac{1}{2} d t_K \frac{d v_{A^{\prime}}^2}{c^2} \)
In Einstein’s example, he labeled the incremental speed of the moving clock (what we call dv-sub-A’) simply v. And so, he obtained a difference in final clock readings of, one half dt times v-squared over c-squared when ignoring the Taylor series expansion terms of fourth order and higher.
\(\text { (difference in final clock readings) } \approx \frac{1}{2} d t \frac{v^2}{c^2} \)
Beautiful! We completely agree with Einstein for once :). Interestingly, this concept actually sparked discussions in 1911 that led to “The Twin Paradox”, which we cover in Episode 10.
So, if Einstein was correct, then the difference in the readings of Clocks A’ versus B’ should be an observable and quantifiable end-state when they unite.
Good, we have a testable experiment!
And if the principle of relativity is true, then the difference in final clock readings should be the same regardless of whether we perform the experiment in system capital-K, or System small-k, or System S, or System S’, etc.; because, according to Special Relativity and the Lorentz transforms, we should always be able to swap a stationary system for a moving system, and vice versa.
So, for any given speed at which Clock A’ travels through System S’ toward Clock B’, we should always find Clocks A’ and B’ to report the same measurable difference in the readings when they unite, whether System S’ is considered moving or stationary.
According to Special Relativity, the laws of physics should be the same regardless of the inertial system.
So, let’s take our formula for the difference in clock readings, and make some substitutions so that we can determine if the difference in readings on Clocks A’ and B’ remains constant regardless of the speed of System S’ relative to System K.
\(d t^{\prime}{ }_{\left(\text {clocks } B^{\prime} v s \hspace{0.1cm} A^{\prime} \Delta\right)}=d t_K\left(\sqrt{1-\frac{v_{S^{\prime}}^2}{c^2}}-\sqrt{1-\frac{v_{A^{\prime}}^2}{c^2}}\right)-\frac{v_{S^{\prime}} d x^{\prime}}{c^2} \)
First, we note that the Lorentz time transform for elapsed time on Clock B’ can be written as, dt-sub-K measured on a System K clock times the square root of 1 minus v-sub-S’ squared over c-squared minus the clock offset term.
\(d t_{B^{\prime} \Delta}^{\prime}=d t_K \sqrt{1-\frac{v_{S^{\prime}}^2}{c^2}}-\frac{v_{S^{\prime}} d x^{\prime}}{c^2} \)
The difference in the readings on Clocks A’ versus B’ can then be written as, dt’-sub-B’ (as adjusted for clock offset), minus dt measured on Clock K times the square root of 1 minus the speed of Clock A’ with respect to System K squared over c-squared.
\(d t^{\prime}{ }_{\left(\text {clocks } B^{\prime} v s \hspace{0.1cm} A^{\prime} \Delta\right)}=d t_{B^{\prime} \Delta}^{\prime}-d t_K \sqrt{1-\frac{v_A^2}{c^2}} \)
And then, because, and only because, Clocks A’ and B’ were Einstein-synchronized at the outset, we can use the following identity,
\(\frac{\gamma_{v_A^{\prime}{\prime}}}{\gamma_{v_A{\prime}} \gamma_{v_{S^{\prime}}}}=1-\frac{v_A v_{S^{\prime}}}{c^2} \)
which can be derived from the invariant interval,
\(c^{\prime 2} d t^{\prime 2}-d x^{\prime 2}=c^2 d t^2-d x^2 \)
\(\frac{d t^{\prime}}{d t}=\frac{\gamma_{v_A^{\prime}{\prime}}}{\gamma_{v_{A^{\prime}}}} \)
in addition to the inverse of Einstein’s velocity addition formula,
\(v^{\prime}_{A^{\prime}}=\frac{v_{A^{\prime}}-v_{B^{\prime}}}{1-\frac{v_{A^\prime} v_{B^\prime}}{c^2}} \)
to arrive at the following intermediary formula for dt-prime-sub-B-prime-delta.
\(d t_{B_{\Delta}^{\prime}}^{\prime}=\frac{d x^{\prime}}{v^\prime_{A^{\prime}}}=d x^\prime \frac{\left(1-\frac{v_{A^\prime} v_{S^{\prime}}}{c^2}\right)}{v_{A^{\prime}-v_{S^{\prime}}}}=\frac{\gamma_{v_{A^{\prime}}^{\prime}}}{\gamma_{v_{A^{\prime}}} \gamma_{v_{S^{\prime}}}} \frac{d x^{\prime}}{v_{A^{\prime}}-v_{S^{\prime}}} \)
Please note that Einstein’s velocity addition formula, and its derivatives, require the use of clocks that have been offset using Einstein’s unusual synchronization protocol. Use of this formula is not appropriate for setups in which there is only one clock present, such as in a Sagnac experiment, or when clocks have been absolutely synchronized.
\(\frac{\color{#e97031}{d t^\prime_{B^{\prime}\Delta}}}{\color{#196b23}{\gamma_{v^{\prime}{ }_{A^{\prime}}}}}=\frac{1}{\color{#9f2b92}{\gamma_{v_{A^{\prime}}}}}\color{#01afef}{ \frac{\frac{d x^\prime}{\gamma_{v_{S^{\prime}}}}}{\left(v_{A^{\prime}}-v_{S^{\prime}}\right)}} \)
Now we can spot a formula for dt-sub-K, the term in the blue box, in this intermediate formula. The following is merely a variation of a formula that Einstein published in his 1905 relativity paper.
\(\color{#01afef}{d t_K=\frac{\frac{d x^{\prime}}{\gamma_{v_{S^{\prime}}}}}{\left(v_{A^{\prime}}-v_{S^{\prime}}\right)}} \)
The time elapsed on Clock K is equal to the length-contracted distance traveled by Clock A’, dx’ divided by gamma-sub-v-sub-S’, divided by the amount by which the speed of Clock A’ exceeds the speed of Frame S’.
\(\frac{\color{#e97031}{d t_{B^{\prime} \Delta}^{\prime}}}{\color{#196b23}{\gamma_{v^{\prime}{ }_{A^{\prime}}}}}=\frac{1}{\color{#9f2b92}{\gamma_{v_{A^{\prime}}}}}\color{#01afef}{ \frac{\frac{d x^\prime}{\gamma_{v_{S^{\prime}}}}}{\left(v_{A^{\prime}}-v_{S^{\prime}}\right)}}=\frac{1}{\color{#9f2b92}{\gamma_{v_{A^{\prime}}}}} \color{#01afef}{ d t_K}=\frac{\color{#01afef}{d t_K}}{\color{#9f2b92}{\gamma_{v_{A^{\prime}}}}} \)
We can then rearrange our formula for dt-prime-sub-B-prime-delta, to arrive at the conclusion that the time that elapses on Clock B’ times the inverse of the Lorentz factor evaluated at the speed of Clock A’ with respect to System S’, is equal to the time that elapses on Clock K times the inverse of the Lorentz factor evaluated at the speed of Clock A’ with respect to System K.
\(\color{#e97031}{d t_{B^{\prime} \Delta}^{\prime}} \color{#196b23}{\sqrt{1-\frac{v_{A^{\prime}}^{\prime 2}}{c^2}}}=\color{#01afef}{d t_K} \color{#9f2b92}{\sqrt{1-\frac{v^2_{A^{\prime}}}{c^2}}} \)
The formula for the difference in clock readings can then be rewritten as, dt-prime-sub-B’-delta times 1 minus the square root of 1 minus v-prime-sub-A’ squared over c-squared.
\(d t^{\prime}{ }_{\left(\text {clocks } B^{\prime} v s\hspace{0.1cm} A^{\prime} \Delta\right)}=d t_{B^{\prime} \Delta}^{\prime}-d t_{B^{\prime} \Delta}^{\prime} \sqrt{1-\frac{v_{A^{\prime}}^{\prime 2}}{c^2}}=\color{#4fa72d}{d t_{B^{\prime} \Delta}^{\prime}\left(1-\sqrt{\left.1-\frac{v_{A^{\prime}}^{\prime 2}}{c^2}\right)}\right.} \)
We can then approximate this to second order with a Taylor series expansion,
\(d t^{\prime}{ }_{\left(\text {clocks } B^{\prime} v s\hspace{0.1cm} A^{\prime} \Delta\right)} \approx d t_{B^{\prime} \Delta}^{\prime}\left(1-1+\frac{v_{A^{\prime}}^{\prime 2}}{2 c^2}\right) \approx \frac{1}{2} d t_{B^{\prime} \Delta}^{\prime} \frac{v_{A^{\prime}}^{\prime 2}}{c^2} \)
and arrive at Einstein’s formula written with respect to both System S’ variables and System K variables.
\(d t^{\prime}{ }_{\left(\text {clocks } B^{\prime} v s\hspace{0.1cm} A^{\prime} \Delta\right)} \approx \color{#e97031}{\frac{1}{2} d t_{B^{\prime} \Delta}^{\prime} \frac{v_{A^{\prime}}^{\prime 2}}{c^2}} \approx \color{#01afef}{ \frac{1}{2} d t_K \frac{v_{A^{\prime}}^2}{c^2}} \)
In other words, Einstein’s formula works whether we measure time and speed in System S’ or System K, regardless of the speed of either system with respect to the other.
And since dt’ for Clock B’ is equal to dx’ over v-prime-sub-A’, we see that the difference in clock readings will remain constant, provided that we choose a fixed v-prime-sub-A’, irrespective of the speed of System S’,
\(d t_{B^{\prime} \Delta}^{\prime}=\frac{d x^{\prime}}{v_{A^{\prime}}^{\prime}} \)
\(d t^{\prime}{ }_{\left(\text {clocks } B^{\prime} v s\hspace{0.1cm} A^{\prime} \Delta\right)} \approx \frac{1}{2} d x^{\prime} \frac{\color{#196b23}{v^\prime_{A^{\prime}}}}{c^2} \)
and also, and this is extremely important, provided that v-prime-sub-A’ was measured in System S’ using distant clocks that had been Einstein-synchronized at the outset.
Again, we find that the principle of relativity holds true under these conditions. The difference in clock readings is independent of the speed of System S’ provided that Clock A’ speed is a fixed quantity within System S’, and, that Einstein-synchronized clocks are used to measure times and to compute speeds in System S’.
So, once again, Einstein succeeds. He conjured up a method that appears to preserve the principle of relativity, provided we follow his rules regarding the use and synchronization of distant clocks.
But what if we could design an experiment that makes the offset of clocks irrelevant?
Would the principle of relativity still hold true? The clock offset is only required by Special Relativity Theory when we measure one-way trips in the moving system along the axis of motion, what we call the x’-axis in System S’. But what if we make round-trip measurements instead?
In which case the downstream and upstream clock offsets cancel each other exactly.
The answer, I promise you, is going to be fascinating.
But first, we must dispense with an objection typically raised in the story of The Twin Paradox, where a moving clock partaking in a round-trip journey must change direction at some point to return to its origin.
If we can avoid the changing of direction, or otherwise accelerating or decelerating our clocks, we can avoid these objections.
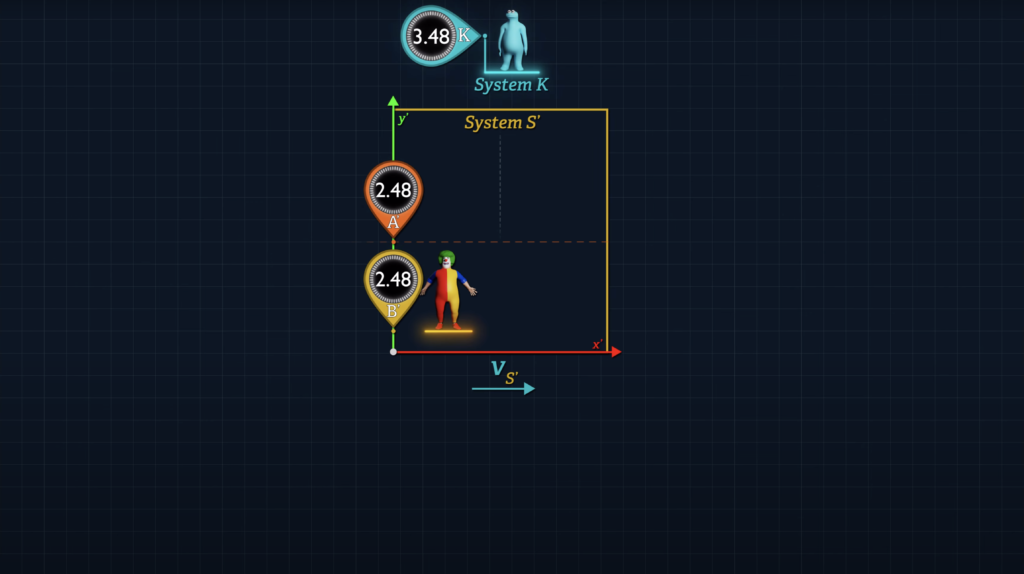
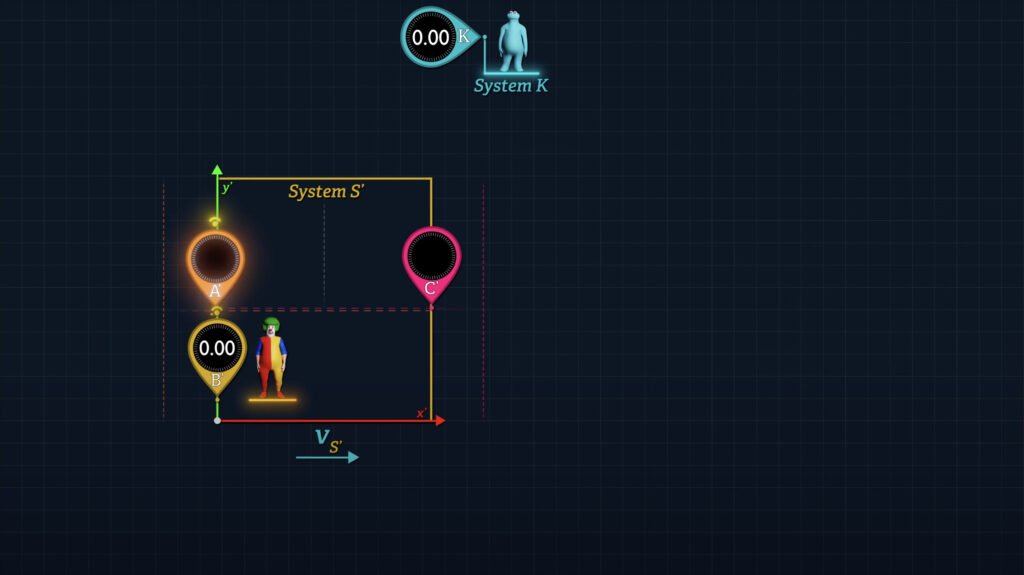
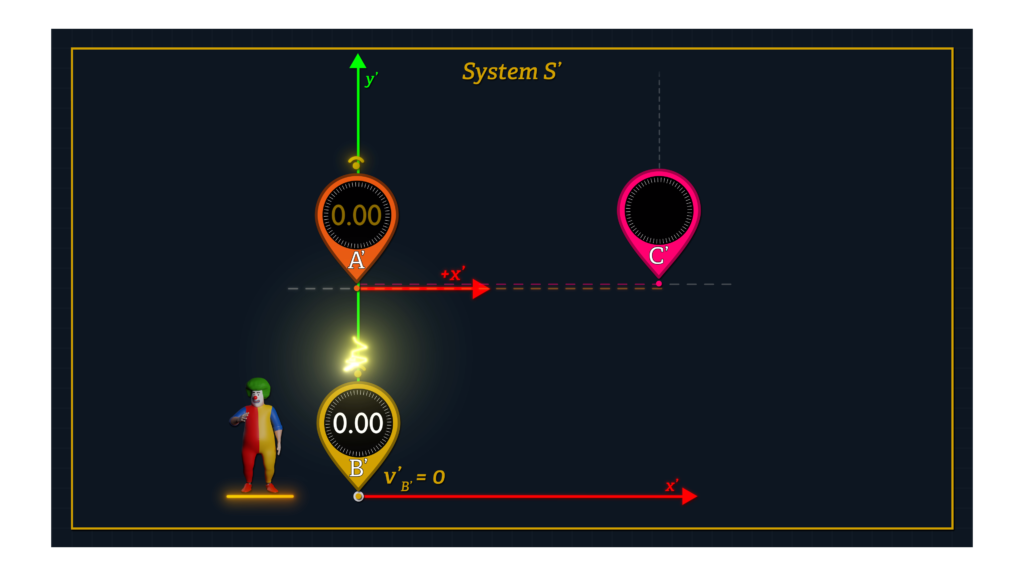
Let’s use a little creativity with Clocks A’ and B’. Let’s say that Clock B’ is stationary at the origin of System S’ as before. But now let’s consider a Clock A’ as moving along the x’-axis parallel to the direction of System S’ motion.
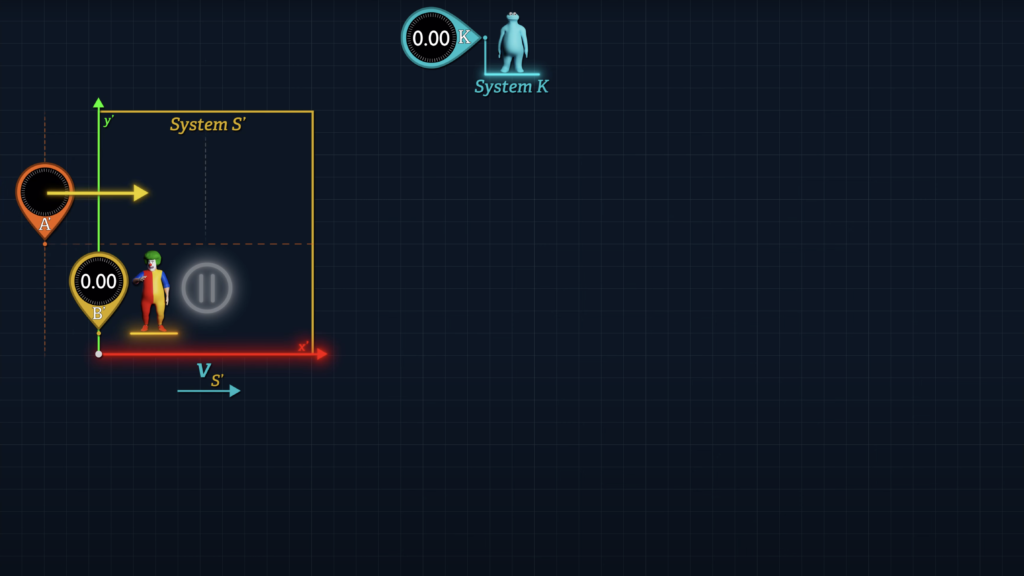
When Clock A’ reaches Clock B’ at the S’ origin, Clocks A’ and B’ are synchronized.
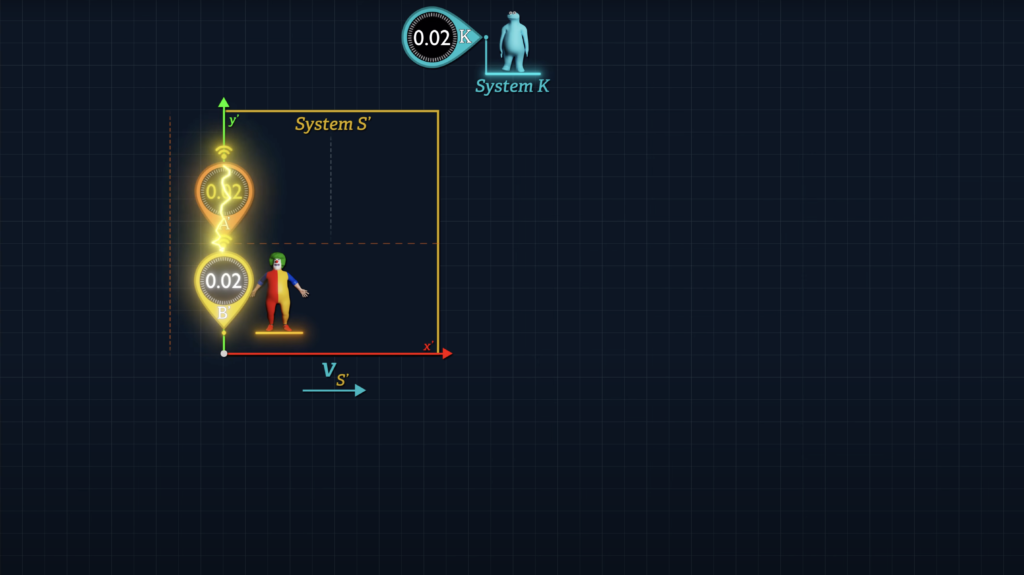
Note that if we use Einstein’s synchronization method under conditions where the distance between these clocks is zero, both clocks will report the same clock reading, regardless of the speed of System S’ relative to System K.
We can even reflect this in our master formula for determining the difference in clock readings.
\(d t^{\prime}{ }_{\left(B^{\prime} v s\hspace{0.1cm} A^{\prime}\right)}=d t_K\left(\sqrt{1-\frac{v_{B^{\prime}}^2}{c^2}}-\sqrt{1-\frac{v_{A^{\prime}}^2}{c^2}}\right)-\frac{v_{S^{\prime}}\color{#ea3324}{ * 0}}{c^2}=d t_K\left(\sqrt{1-\frac{v_{B^{\prime}}^2}{c^2}}-\sqrt{1-\frac{v_{A^{\prime}}^2}{c^2}}\right) \)
So, whether we use Einstein’s synchronization method, or the simple matching of clock readings at the origin, we’ve synchronized Clocks A’ and B’ to report exactly the same time reading at the instant they are side by side.
Next, we’d like to measure the speed of Clock A’ in System S’ without resorting to the use of distant clocks that have been offset with Einstein’s clock synchronization method.
Why? Well, it’s not widely appreciated, but use of such offset clocks will bias the computation of travel speeds.
The use of distant, offset clocks to measure elapsed time can deceive observers in System S’ into believing that identical downstream and upstream speeds are not identical; or that non-identical downstream and upstream speeds are identical – which is the trick that Einstein used to convince observers in moving systems that light travels at a constant speed c in either direction.
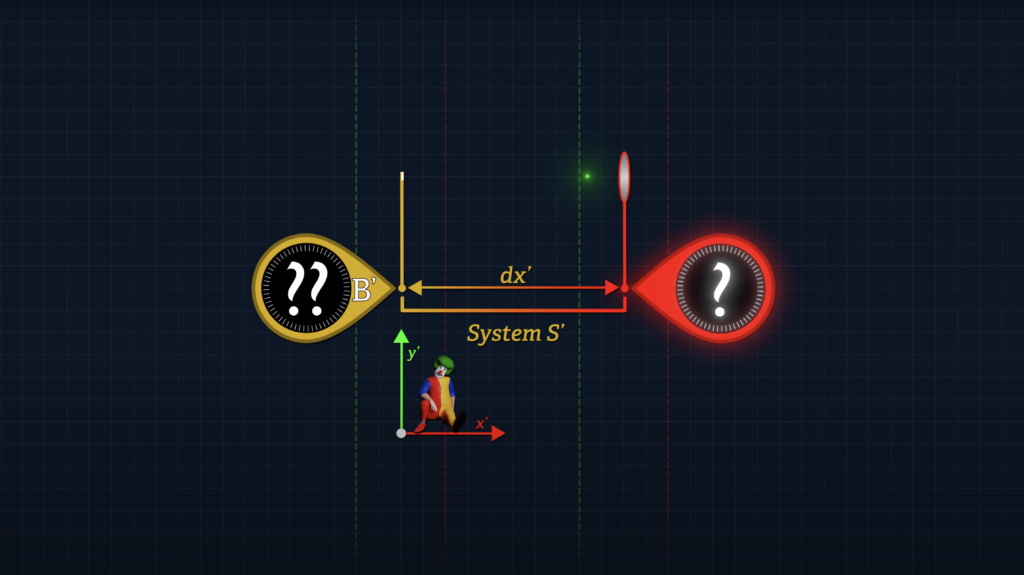
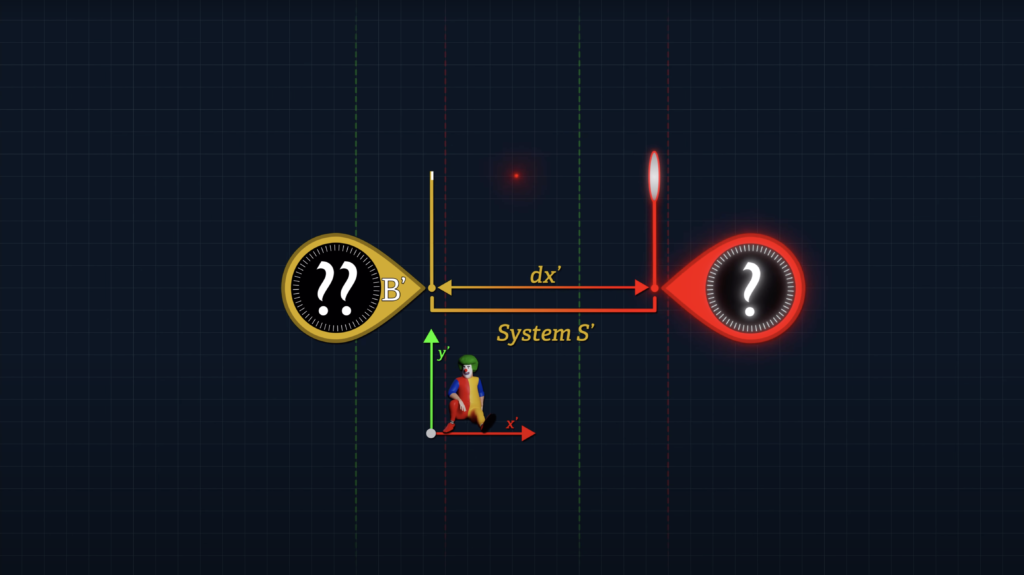
And unless one intends to manipulate time measurements to satisfy some pre-conceived postulates, there is no need to use distant, offset clocks to measure speeds and times, when local measurements will suffice.
Observers in Einstein’s stationary System K do not require distant, offset clocks to determine the speed v of another system. They can simply measure the speed of another system passing a single clock that is stationary in System K.
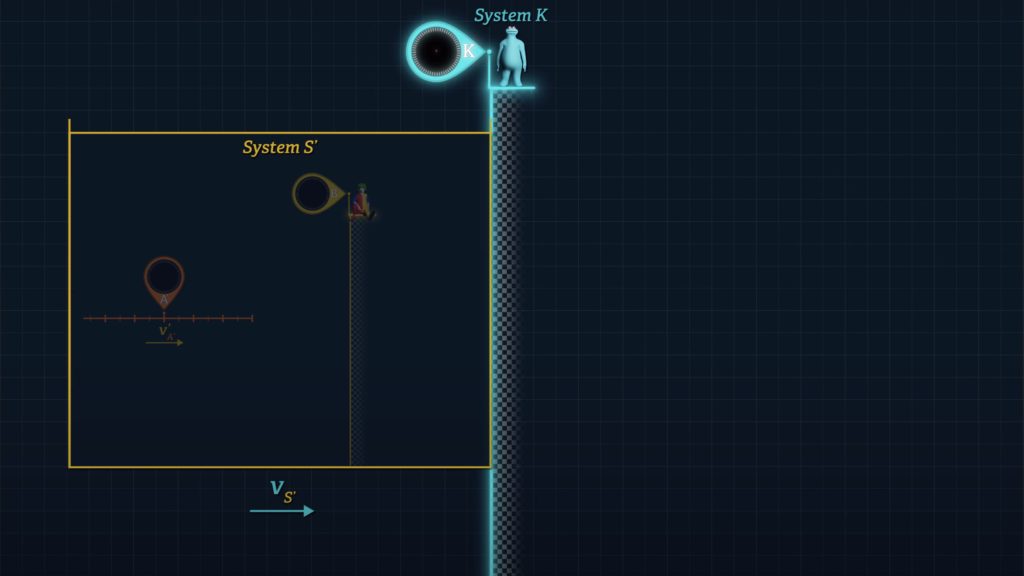
We can choose to do the same in System S’ such that a single clock in S’ is used to measure elapsed times in order to compute Frame S’ speeds. If Clock A’ were aboard let’s say a spaceship of known proper length in System S’, we can divide its proper length by the amount of time that elapses on Clock B’ from the instant the front of the ship passes Clock B’ to the instant the rear of the ship passes Clock B’.
So how do we measure round-trip durations without accelerating or decelerating any of the clocks? Let’s add another Clock, C’.
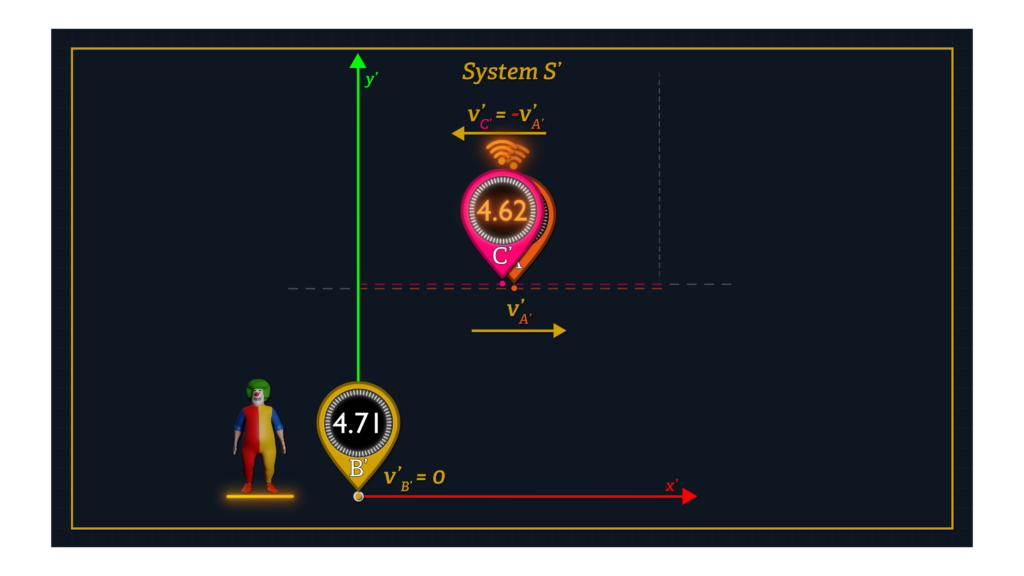
Clock C’ happens to be traveling within System S’ at the same speed as Clock A’, but in the opposite direction. As with Clocks A’ and B’, Clock C’ speed is measured using a single clock in System S’ and a single clock in System K.
When Clocks A’ and C’ cross paths, observers in System S’ can measure the proper distance dx’1 from that location to the S’ origin using System S’ measuring tools.
Furthermore, when Clocks A’ and C’ cross paths, Clock A’ sends a time-stamped signal to Clock C’. In other words, information is transferred from Clock A’ to Clock C’, communicating the reading on Clock A’ at that instant. Clock C’ records its own time reading at that instant and, in order to make our future computations slightly easier, re-sets its own clock reading to the exact time reported by Clock A’. Clock C’ has essentially been Einstein-synchronized with Clock A’ when they meet, again without producing a clock offset.
No clocks change direction or speed. No offsets are introduced into any of our clocks to distort or to artificially manipulate the outcome of time or speed measurements.
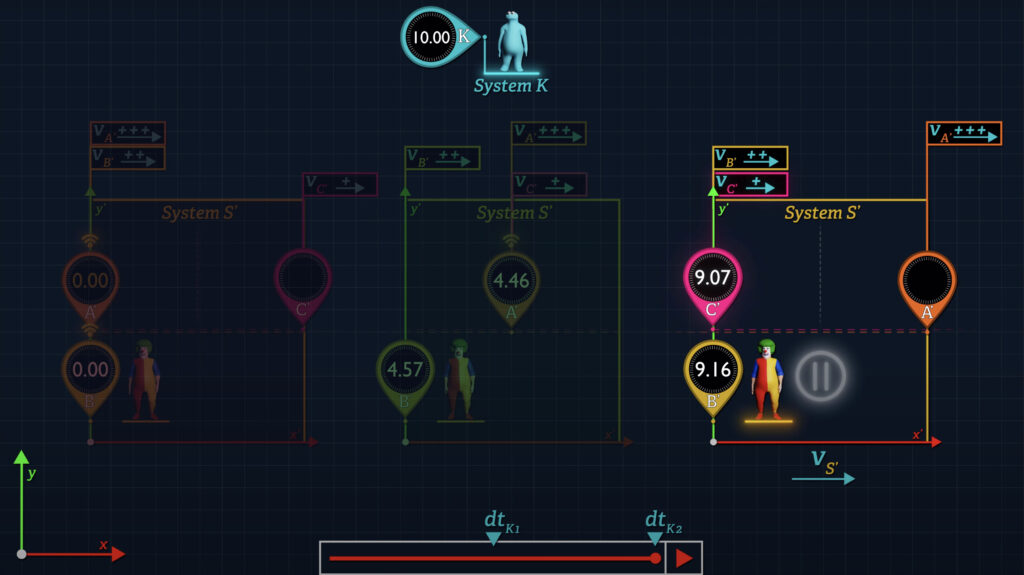
And as you can see in the animation, when all three clocks move in the positive x-direction in System K, Clocks A’ and B’ begin side by side, whereas Clock C’ begins slightly downstream. Clock A’ moves faster than Clock B’, which moves faster than Clock C’.
After time dt-sub-K1 Clock A’ reaches Clock C’, and Clock A’ shares its time reading with Clock C’. Clock B’ has not moved as far as Clock A’ during this period. But after additional time dt-sub-K2, Clock B’ approaches Clock C’, where they compare time readings.
In contrast, from the perspective of System S’, Clock B’ is stationary, Clock A’ moves in the positive x’-direction at speed v-prime-sub-A’, and Clock C’ moves in the negative x’-direction at the same speed as Clock A’. Again, offset clocks are avoided in the computation of Clock A’ and C’ speeds in System S’, and the use of Einstein’s relativistic velocity addition formula is also avoided since it requires that time measurements be made with the use of offset clocks.
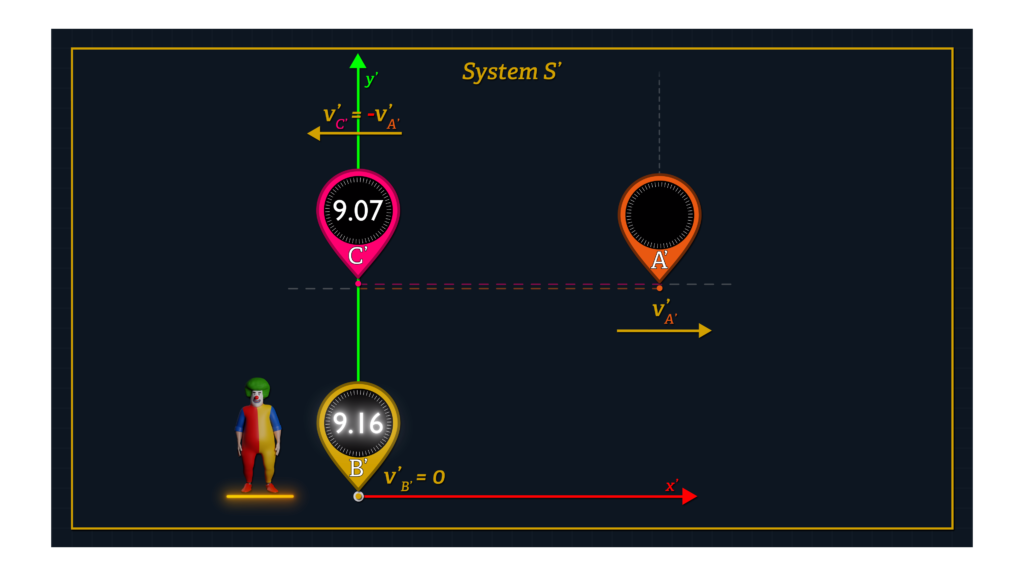
Clocks A’ and C’ meet after Clock A’ has traveled a distance dx’1 and then Clock C’ proceeds in the negative x’-direction until it meets Clock B’, where they compare clock readings.
The question we wish to ask is whether the difference in the time readings of clocks C’ versus B’ will be the same or different for any given speed of System S’. So, we need to solve for the readings on Clocks A’, B’, C’, and K.
When clock offset is not used, the formula for time in System K is, gamma-sub-v-sub-S’ times the round-trip time elapsed on Clock B’.
\(d t({ round trip })=d t_{K 1}+d t_{K^2}=\gamma_{v_{s^{\prime}}}\left(\frac{d x_1^{\prime}}{v_{A^{\prime}}^{\prime}}+\frac{d x_2^{\prime}}{v_{C^{\prime}}^{\prime}}\right)=\gamma_{v_{s^{\prime}}} d t_{B^{\prime} \text { round trip }}^{\prime} \)
And since dx’1 is equal to negative dx’2, and v-prime-sub-A’ is equal to negative v-prime-sub-C’, each leg of the trip is of equal duration in both systems K and S’. And so dtK1 is equal to dtK2.
In his 1905 relativity paper, Einstein gave us formulas that we can use for the time elapsed on Clock K for each leg of the trip.
\(d t_{K 1}=\frac{d x_1^{\prime}}{\gamma_{v_{S^{\prime}}}\left(v_{A^{\prime}}-v_{S^{\prime}}\right)} \)
\(d t_{K 2}=\frac{d x_2^{\prime}}{\gamma_{v_{S^{\prime}}}\left(v_{C^{\prime}}-v_{S^{\prime}}\right)} \)
We can solve for v-sub-A’ and v-sub-C’ using the following defined terms, keeping in mind that v-prime-sub-A’ and v’-prime-sub-C’ are determined using a single clock to measure elapsed time in System S’.
\(\color{#d86cca}{v_{A^{\prime}}^{\prime}=\frac{d x_1^{\prime}}{d t_{B^{\prime} 1}^{\prime}}} \text { and } \color{#9f2b92}{v_{C^{\prime}}^{\prime}=\frac{d x_2^{\prime}}{d t_{B^{\prime} 2}^{\prime}}} \)
\(\color{#34749d}{v_{A^{\prime}}}=d v_{A^{\prime}}+v_{S^{\prime}}=\frac{d x_1^{\prime}}{\gamma_{v_{S^{\prime}}} d t_{K 1}}+v_{S^{\prime}}=\frac{\color{#d86cca}{d x_1^{\prime}}}{\gamma_{S^{\prime}}^2 \color{#d86cca}{d t_{B^{\prime} 1}^{\prime}}}+v_{S^{\prime}}=\frac{\color{#d86cca}{v_{A^{\prime}}^{\prime}}}{\gamma_{S^{\prime}}^2}+v_{S^{\prime}} \)
\(\color{#e97031}{v_{C^{\prime}}}=d v_{C^{\prime}}+v_{S^{\prime}}=\frac{d x_2^{\prime}}{\gamma_{v_{S^{\prime}}} d t_{K 2}}+v_{S^{\prime}}=\frac{\color{#9f2b92}{d x_2^{\prime}}}{\gamma_{S^{\prime}}^2 \color{#9f2b92}{d t_{B^{\prime} 2}^{\prime}}}+v_{S^{\prime}}=\frac{\color{#9f2b92}{v_{C^{\prime}}^{\prime}}}{\gamma_{S^{\prime}}^2}+v_{S^{\prime}} \)
And since dtK1 is equal to dtK2, and dx’1 is equal to negative dx’1, the amount by which v-sub-A’ exceeds v-sub-S’ in System K will be the same as the amount by which v-sub-C’ is less than v-sub-S’ in System K. In other words, speeds v-sub-A’ and v-sub-C’ are symmetric around speed v-sub-S’ in System K.
Since no acceleration or deceleration takes place in our round-trip model, and since Clocks A’ and B’ were synchronized to exactly the same time reading at the start of the experiment, and Clocks A’ and C’ were synchronized to exactly the same time reading when they met, the difference in clock readings on clocks B’ and C’ when they eventually meet will be due solely to the differences in clock tempos, which according to Special Relativity are governed by the speeds of the clocks relative to System K.
\(d t^{\prime}{ }_{\left(B^{\prime}v s \hspace{0.1cm}C^{\prime}\right)}=d t_{K 1} \sqrt{1-\frac{v_{B^{\prime}}^2}{c^2}}+d t_{K 2} \sqrt{1-\frac{v_{B^{\prime}}^2}{c^2}}-d t_{K 1} \sqrt{1-\frac{v_{A^{\prime}}^2}{c^2}}-d t_{K 2} \sqrt{1-\frac{v_{C^{\prime}}^2}{c^2}} \)
When we require Clocks A’ and C’ to travel at the same speed relative to a single clock in System S’, for example relative to Clock B’, then dtK1 and dtK2 will be equal.
We can then condense this formula to the following formula,
\(d t^{\prime}{ }_{\left(B^{\prime} v s\hspace{0.1cm} C^{\prime}\right)}=2 d t_{K 1} \sqrt{1-\frac{v_{S^{\prime}}^2}{c^2}}-d t_{K 1} \sqrt{1-\frac{\left(v_{S^{\prime}}+d v_{A^{\prime}}\right)^2}{c^2}}-d t_{K 2} \sqrt{1-\frac{\left(v_{S^{\prime}}-d v_{C^{\prime}}\right)^2}{c^2}} \)
where dv-sub-A’ and dv-sub-C’ represent the differential System K speeds of Clocks A’ and C’ with respect to the speed of System S’ (which is also the speed of Clock B’).
\(d v_{A^{\prime}}=\frac{v_{A^{\prime}}^{\prime}}{\gamma_{S^{\prime}}^2}=\frac{v_{C^{\prime}}^{\prime}}{\gamma_{S^{\prime}}^2}=d v_{C^{\prime}} \)
We find that the formula for the difference in Clock B’ versus Clock C’ readings is not independent of the speed of System S’!
\(d t^{\prime}{ }_{\left(B^{\prime} v s\hspace{0.1cm} C^{\prime}\right)}=2 d t_{K 1} \sqrt{1-\frac{v_{S^{\prime}}^2}{c^2}}-d t_{K 1} \sqrt{1-\frac{\left(v_{S^{\prime}}+\frac{v_{A^{\prime}}^{\prime}}{\gamma_{S^{\prime}}^2}\right)^2}{c^2}}-d t_{K 2} \sqrt{1-\frac{\left(v_{S^{\prime}}-\frac{v_{C^{\prime}}^{\prime}}{\gamma_{S^{\prime}}^2}\right)^2}{c^2}} \)
\(d t^\prime_{\left(B^{\prime} vs\hspace{0.1cm} C^\prime\right)}=d t_{K 1}\left(2 \sqrt{1-\frac{v^2_{S^{\prime}}}{c^2}}-\sqrt{1-\frac{\left(v_{S^{\prime}}+\frac{v_{A^{\prime}}^{\prime}}{\gamma_{S^{\prime}}^2}\right)^2}{c^2}}-\sqrt{1-\frac{\left(v_{S^{\prime}}-\frac{v_{C^{\prime}}^{\prime}}{\gamma_{S^{\prime}}^2}\right)^2}{c^2}}\right) \)
Now let’s study this formula for a minute. When Clock C’ reaches Clock B’ it will report a different time than what is being displayed on Clock B’. In fact, Clock B’ will always be slightly ahead of Clock C’ since the formula must yield a positive number unless v-prime-sub-A’ and v-prime-sub-C’ are both zero.
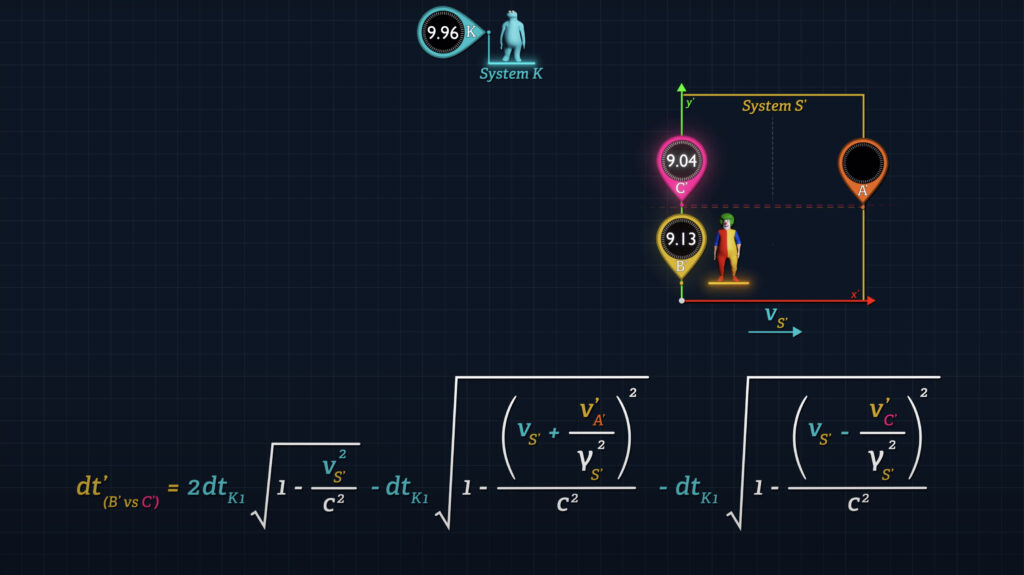
This is the real answer to “The Twin Paradox”, which is not really a paradox once one understands that the symmetry assumed in Special Relativity is a deeply flawed concept. Acceleration and deceleration are completely unnecessary for one clock to have “aged” less than another clock. The effect is greatest when v-prime-sub-A’ and v-prime-sub-C’ are large compared to v-sub-S’; and least when v-prime-sub-A’ and v-prime-sub-C’ are small compared to v-sub-S’.
Even when System S’ itself is stationary such that v-sub-S’ is zero, Clock C’ will display a reading that is behind Clock B’ when they meet. In fact, the effect is greatest when v-sub-S’ is zero.
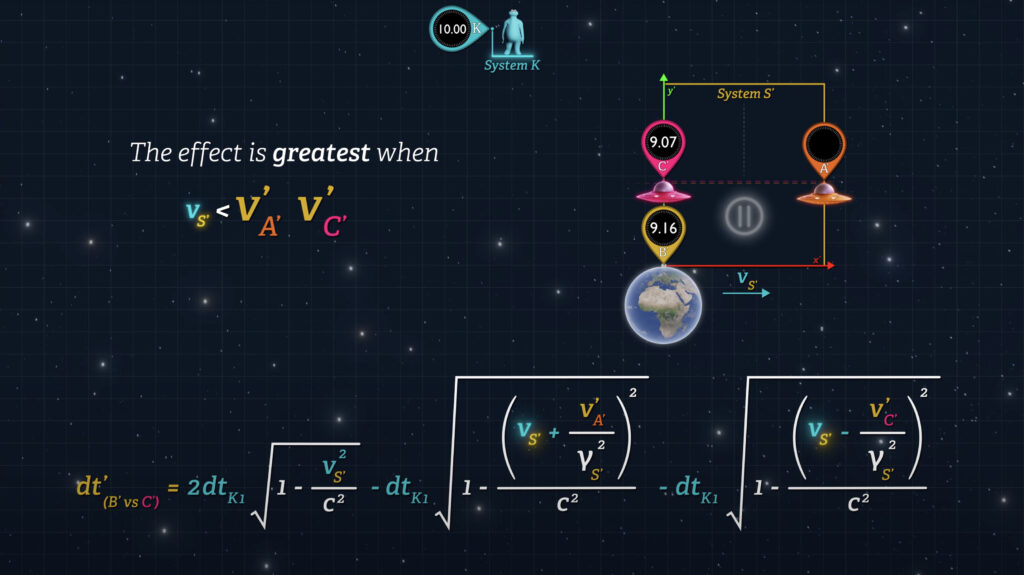
So, if the Earth is stationary in the universe (v-sub-S’ = 0) and an outbound spaceship (Spaceship A) synchronizes clocks with an inbound spaceship (Spaceship B) while they are both in space, the clocks on the inbound spaceship (Spaceship B) will lag behind Earth-clocks when it returns.
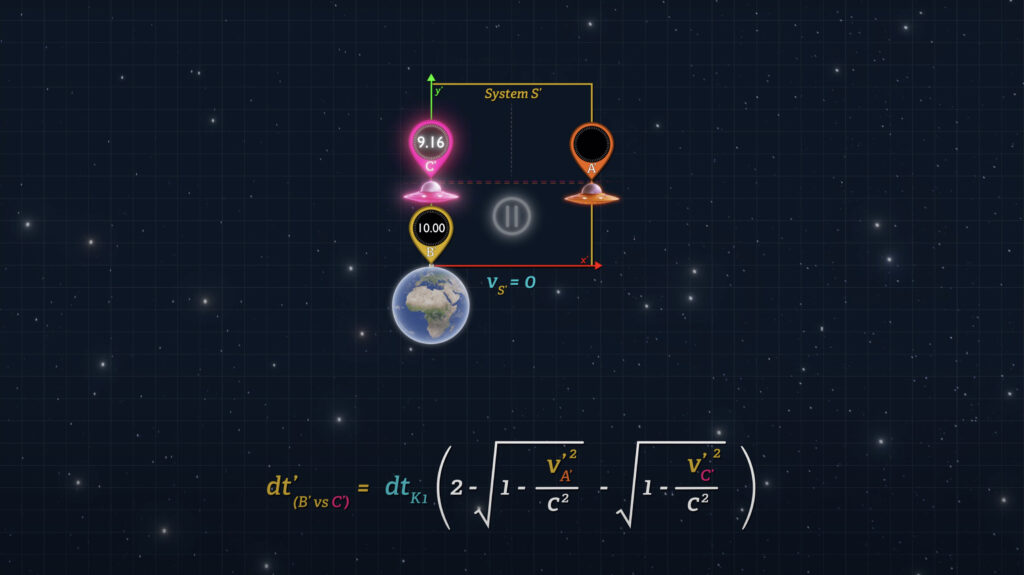
But if the Earth is moving rapidly through the universe, and the speeds of the spaceships are slow relative to Earth’s universal speed, then the clocks on the inbound spaceship will lag less than if the Earth were stationary in the universe.
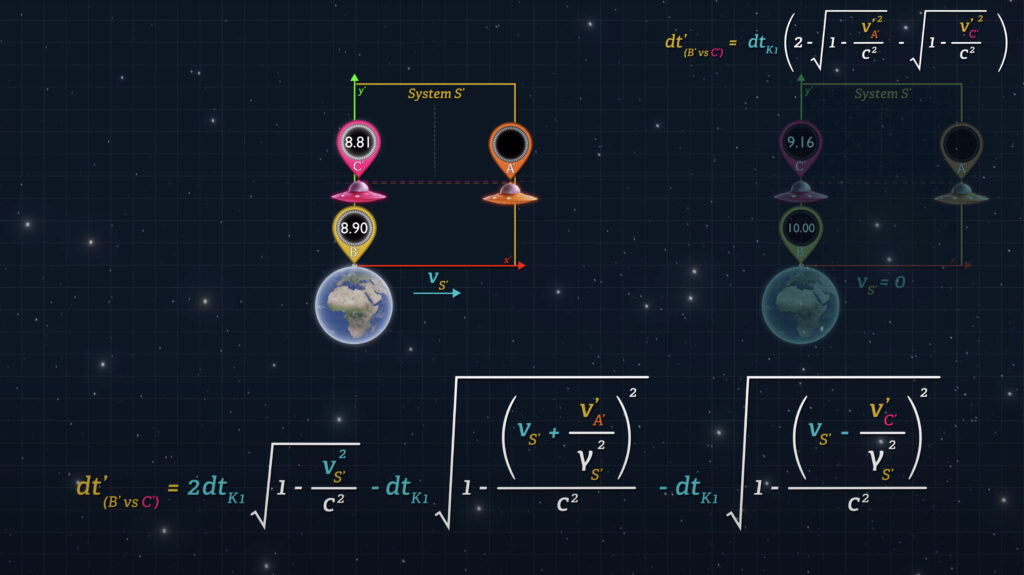
In other words, the difference between the readings on Clocks B’ and C’ when they meet will vary depending on the speed of System S’ with respect to our reference System K. This difference in clock readings is a measurable end-point within a single system. It’s not some illusion subject to the biases of the Relativity of Simultaneity. This unexpected result has been attained by adherence to the rules of Special Relativity, simply by choosing to measure System S’ clock speeds with a single reference clock rather than distant offset clocks.
I mean, obviously, observers in System S’ are free to use whatever tools are available to them in System S’. To force the use of offset clocks instead of a single reference clock is like choosing to dress oneself in front of a fun-house mirror. This might help one to purposely gain or lose weight, but have no doubt that this would be a deceptive trick to distort reality. Why distort reality when we don’t have to?
OK, what does this mean? Shockingly, it means that Special Relativity does not support the principle of relativity for all setups. It means that observers in System S’ will be able to determine an absolute speed for System S’. It means that in order for Relativity to make rational sense, the speed of any inertial system must be measured with respect to some universal, preferred system of reference, and not with respect to some arbitrary reference System K. And if one measures the speeds of Clocks A’ and C’ relative to System S’, one will be able to predict the speed of System S’ relative to that universal preferred inertial system.
This has enormous implications for our universe. If time dilation as described by Einstein is real, it means that there is some universal reference system that grounds the laws of physics.
The laws may be the same everywhere, but the measurements of the variables used in these laws must take into account the speed of the inertial system relative to the universal preferred system.
And that has enormous implications for any physical “constant” that includes time as one of its dimensional components. “Constants” such as Planck’s constant, electric permittivity, magnetic permeability, light speed etc. to name a few, are “constants” that will most likely require recalibration with respect to the speed of the inertial system in which they are measured.
Alright, that’s it for now. Please leave questions in the comments section. And please rate the video favorably if I at least made you think. I’m Joe Sorge, and thanks for watching.