In this episode we’re going to develop some new tools that will give us an intuitive understanding for how light propagates. We’re then going to use these tools to explain why the refractive index of a substance changes the outcome of a Fizeau experiment (see Episode 9.3 for the basics) but does not change the outcome of a Sagnac experiment (see Episode 7.3 for the basics). This will give us some valuable insight into how a refractive medium slows the overall speed of light.
Before we can understand why light travels more slowly through glass or water, we need to talk about one-way vs. two-way light speed measurements, and how Einstein made them come out to be the same speed c.
Now there’s a great Veritasium video where Derek explains why it’s so difficult, if not impossible, to measure the one-way speed of light. It’s called “Why Nobody Has Measured the Speed of Light”. I highly recommend it. The video points out that the challenge to measuring these speeds is not due to the sensitivity or precision of the measuring instruments. The problem has to do with clock synchronization.
So, let’s think about what it would take to measure the one-way speed of light.
Let’s say there is someone on that hilltop over there with a light detector, and we’re over here with a light source. And we want to record the time when we turn on our light signal, and we want the person over there to record the time that the light signal hits the receptor.
The challenge comes from the synchronization of our two clocks. How do we know that our clock and their clock are reporting exactly the same time of day? I mean after all its only going to take a few millionths of a second for light to go from here to there.
So, if the clocks do not report exactly the same time of day, we will not get an accurate measurement.
So, we need some way to coordinate the clocks.
If I yell over there, it’s going to take a few seconds for the sound to travel there. So that won’t work.
If I wave my hands, it’s going to take an unknown amount of time for my image to get over to that hilltop. So that won’t work.
I could shine a light at an agreed upon clock time; but again, there will be an unknown delay between emission and reception.
And no, we cannot start with two clocks side-by-side and transport one of the clocks over to the receiver there — for those of you who’ve watched Episode 9.7 you’ll know that differential time dilation will cause the readings on the two clocks to drift apart.And as far as I know, entanglement will not solve the problem either.
So, unless we have an instantaneous way of synchronizing the clocks, the problem seems insurmountable.
So, scientists in the 1800s came up with a different way to measure light speed, with two-way, round-trip measurements. They built a device with a spinning gear, and they shined light through the gear over to a mirror on a distant hilltop. The mirror reflected the light back through the spokes of the spinning gear to a detector.
And as they spun the gear faster and faster, it reached a speed at which the light that traveled between the spokes of the gear would always become blocked by a spoke when it returned from the distant mirror. And so, they calculated the speed of light based on the speed of the spinning gear. And they came up with about 300 million m/s, which is very close to the speed that we recognize light to travel at today.
But I have to emphasize, they were making round-trip measurements, not one-way measurements. The benefit of measuring a two-way, round trip is that you need only one clock, in this case the spinning gear. Clock synchronization is not a problem. But we have to recognize that such a round-trip measurement does not identify the one-way light speeds.
So, why do we even question whether the speed of light going from here to that distant hilltop might be different than the speed of light coming back from the hilltop? I mean, didn’t Einstein say that light travels at the same speed in all directions? Well, I’m not sure what he truly believed, but he needed light speed to be constant to support his Theory of Relativity, under which you could deem any inertial reference frame as a “stationary reference frame”.
In other words, under his Theory of Relativity, any inertial reference frame could be treated like any other inertial reference frame. You could assume that Frame B is in motion relative to Frame A; or you could assume that Frame A is in motion relative to Frame B.


So, he needed to guarantee that one-way light speed measurements, if they ever could be made, would also produce a speed of c.

Otherwise, it would suggest that the principle of relativity is false, and that the universe is comprised of some type of “universal frame of reference” — in other words, some type of “ether”. And that displeased him.
So, Einstein conceived of a way to make one-way light speed measurements come out to the same as two-way round-trip measurements, regardless of how fast any inertial system moves through space. He conjured up a set of equations that would force the computation of light speed to always yield a constant value — whether light truly moved at a constant one-way speed or not.
Frankly, I think this fudge was one of his greatest mistakes. You can learn more about that in Episode 9.8. But for now, let me show you how his light speed fudge works.
Here I am, struggling to get up this steep hill. I’m really moving very slowly. But if I were to turn around and go downhill, I can go much faster.
Now, the point we’re going to make has nothing to do with gravity. We are just using that as an analogy. We could have used a strong wind blowing in my face that way and blowing at my back this way… What we are really trying to point out is different one-way speeds, and then we are going to compute the time-weighted average to get the true speed over the entire round-trip.
Think of my slower uphill speed as being analogous to lightspeed in the direction that Earth moves through space.
And think of my faster downhill speed as being analogous to lightspeed when light travels against the Earth’s direction through space.
In other words, imagine that when I walk slowly, I’m like a light signal pointing in the direction that Earth travels when it orbits the Sun. So, if light is moving through space at speed c, in the same direction that Earth is moving through space, we might expect observers on the earth who possess a “magical”, one-way light speed measuring device, to measure the speed of that light signal to be slower than speed c, simply because the observers are moving together with the Earth in the same direction as the light signal.

Now, if that light bounces off a mirror on a distant hilltop and returns, it will travel opposite to the direction of Earth’s motion.

In this case, observers on the Earth holding our “magical”, one-way measuring device might observe light to move faster than c as it returns.
Let’s put some numbers to my hill example. Let’s say that I walk up the hill at one and one third miles per hour.
\({u’}_{uphill} = 1\frac{1}{3}mph\ = \ \frac{4}{3}mph \)
Well, it’s going to take, three quarters of an hour to hike 1-mile uphill.
\({dt’}_{uphill} = \ \frac{1\ mile}{\frac{4}{3}mph} = \frac{3}{4}hour \)
And let’s say that I walk downhill at 4 miles per hour.
\({u’}_{downhill}\ = \ 4\ mph \)
It’s going to take one quarter of an hour to hike downhill.
\({dt’}_{downhill}\ = \ \frac{1\ mile}{4\ mph} = \frac{1}{4}hour \)
And so, my total distance traveled is 2 miles, and my total time is 1 hour, so I conclude that I’ve walked a speed of 2 miles per hour.
\({u’}_{round\ trip\ average} = \frac{2\ miles}{1\ hour} = 2\ mph \)
But if we had taken a simple average of my two speeds it would be, two and two thirds miles per hour.
\({u’}_{simple\ average}\ = \frac{\frac{4}{3} + 4}{2} = \frac{\frac{16}{3}}{2} = \frac{8}{3} = 2\frac{2}{3} \approx 2.667\ mph \)
And at no point during my journey did I actually travel at that simple average speed of two and two thirds miles per hour. I spent much more time walking uphill slowly than I did walking downhill quickly. So, to get my overall, average speed, we need to compute the time-weighted average of my uphill and downhill speeds.
\({u’}_{TWA} = \frac{\frac{4}{3}mph\ x\ \frac{3}{4}hours\ \ + \ \ 4\ mph\ x\ \frac{1}{4}hours}{\frac{3}{4}\ hour + \frac{1}{4}hour} = 2\ mph \)
And that time-weighted average speed is 2 miles per hour. This is also true for computing the two-way, round-trip speed of light, as we will see shortly.
So, Einstein knew that he was not going to have a problem with round-trip, two-way light speed measurements. They would always yield a time-weighted average of speed c. But what if someone came up with a way to measure one-way light speeds?
Let’s run through an example where I can show you what he did with the clocks to make one-way light speed come out to be the same in all directions.
Let’s go back to our hill climb and I’ll show you how it works.
What if Einstein had adjusted a clock at the top of the hill to show a time 15 minutes earlier than a clock at the bottom of the hill?


In other words, if I started my climb at 12 noon according to the clock at the bottom, the clock at the top will show an adjusted time of 11:45 am at that instant.

I stated earlier that it requires 45 minutes to reach the top. So, when I reach the top of the hill, the clock at the bottom will report a reading of 12:45.

But since Einstein had set the clock at the top of the hill to report a time 15 minutes earlier than the bottom clock, the clock at the top will now report a time of 12:30 instead of 12:45.

This trick might fool me into thinking (if I didn’t have other ways to track time) that it only took 30 minutes for me to walk one-mile up hill. In other words, this would lead me to conclude that I was moving at a speed of one mile in 30 minutes, or 2 miles per hour.
Next, I turn around and walk downhill. I stated earlier that it only requires 15 minutes for me to reach the bottom.
And so, the clock at the bottom will have advanced from a reading of 12:45 (which it was displaying) at the instant I had reached the top of the hill to a reading of 1:00 pm when I return to the bottom.

But since the clock at the top led me to believe that I left the top at 12:30, and the clock at the bottom displayed a reading of 1:00 pm when I reached the bottom, I am again led to believe that 30 minutes elapsed during this leg of the trip. I am tricked into thinking that I traveled 1 mile downhill in 30 minutes, or again moved at a speed of 2 miles per hour.
Do you see how manipulation of the clocks can make it appear that one-way speeds are the same as two-way speeds?
You just have to manipulate the clocks and not really let your observers know that that’s what you did. It’s all there in Einstein’s 1905 relativity paper! Take a look. I know his writings are cryptic, and he tries not to give away his secret too easily, but if you look at the formulas and carefully read what he wrote, it’s crystal clear that he requires the clocks to be reporting different times of day.
In more mathematical terms, Einstein’s clock synchronization protocol creates a spatial gradient of clock readings against the direction of reference frame motion.
Alright, let’s go back to the studio. We’ll work out the math and I’ll prove it to you.
OK, with those basics in mind, it’s time to get back to Fizeau and Sagnac. They will provide the secret sauce to revealing Einstein’s clock trick, because they each have only one device for measuring elapsed travel times — a beam splitter. Sagnac essentially invented the “magical device” for measuring one-way light speeds.
As you may recall, light travels from the beam splitter, where it is split into two, counter-propagating signals that travel around a loop either clockwise or counterclockwise. The signals re-unite at the original beam-splitter and form an interference pattern.
If one signal travels faster than the other signal (with respect to the moving reference frame) the interference pattern shifts.
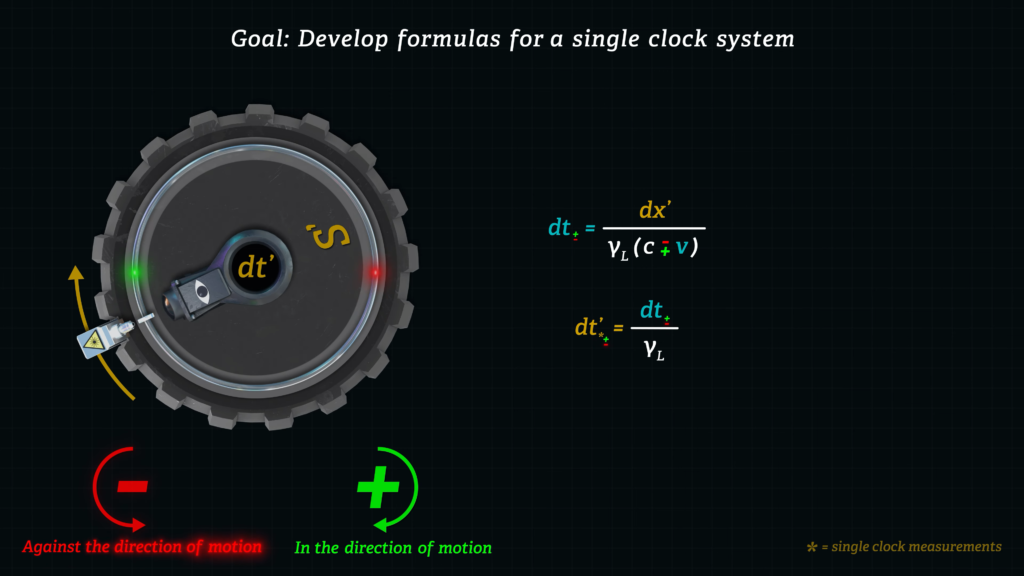
Since a Sagnac device has only one time-measurement mechanism, the beam splitter that produces the interference pattern, we need to develop some formulas that are similar to the Lorentz’s transforms, to keep track of lightspeed, distances, and times, but for a single-clock system.
We can start with one of Einstein’s formulas that does not depend on having two clocks.
\(\color{#01afef}{dt_{\pm} = \frac{dx’}{\gamma_{L}(c \mp v)}} \)
The time elapsed on a clock in what is deemed to be the stationary frame, dt, is equal to the path length in the moving frame, dx’ divided by the Lorentz gamma factor, times light speed, c, minus or plus the speed v of the moving frame through space.
Next, since we are using only one clock, we can assume that the duration measured with a single clock in a moving reference frame will report gamma-times fewer seconds than for the same duration measured with a clock in a stationary reference frame.
\(\color{#f08e37}{dt_{* \pm}^{‘}} = \frac{\color{#01afef}{dt_{\pm}}}{\gamma_{L}} \)
I use the star (*) symbol to alert us that this value of dt’ is for a single clock that has not been biased by Einstein’s clock synchronization convention. I use the plus or minus symbols to designate light traveling either a) in the direction of motion of the moving reference frame, or b) against the direction of motion of that frame.
And so, time elapsed on a single, Earth based-clock, will be the Earth-based proper distance, dx’, divided by the Lorentz gamma factor squared, times light speed, c, minus or plus the speed of the Earth through space, v.
\(\color{#f08e37}{dt_{* \pm}^{‘} = \frac{dx’}{\gamma_{L}^{2}(c \mp v)}} \)
Now, one-way light speed on the Earth, if it could be measured with a single clock, will be equal to distance dx’ divided by duration measured with that single, Earth-based clock. It is equal to speed c divided by one plus or minus the speed of the moving reference frame, v, in proportion to speed c.
\(c_{* \pm}^{‘} = \frac{dx^{‘}}{\color{#f08e37}{dt_{* \pm}^{‘}}} = \frac{{dx}^{‘}}{\color{#f08e37}{\frac{dx’}{\gamma_{L}^{2}(c \mp v)}}} \)
\(c_{* \pm}^{‘} = \gamma_{L}^{2}(c \mp v) \)
\(c_{* \pm}^{‘} = \frac{c}{1 \pm \frac{v}{c}} \)
\(\color{#01afef}{dt_{\pm} = \frac{dx’}{\gamma_{L}(c \mp v)}} \)
\(\color{#34749d}{dt_{* \pm}^{‘} = }\frac{\color{#01afef}{dt_{\pm}}}{\color{#34749d}{\gamma_{L}}}\ \ \ \ \ \ \ \ \ \ \ \ \ \color{#f08e37}{dt_{* \pm}^{‘} =}\color{#34749d}{ \frac{dx’}{\gamma_{L}^{2}(c \mp v)}} \)
\(c_{* \pm}^{‘} = \frac{dx^{‘}}{\color{#f08e37}{dt_{* \pm}^{‘}}}\ \ \ \ \ \ \ \ \ \ \ \ \ c_{* \pm}^{‘} = \frac{{dx}^{‘}}{\color{#f08e37}{\frac{dx’}{\gamma_{L}^{2}(c \mp v)}}}\ \ \ \ \ \ \ \ \ \ \ \ \ c_{* \pm}^{‘} = \gamma_{L}^{2}(c \mp v) \)
\(c_{* \pm}^{‘} = \frac{c}{1 \pm \frac{v}{c}} \)
This formula predicts that an observer with a single clock will measure light to travel slower than c in the moving-frame when it travels in the positive direction, which would be the same direction as Earth’s velocity through space. And it will be the speed of light in a Sagnac device when the light signal and the device move in the same direction.

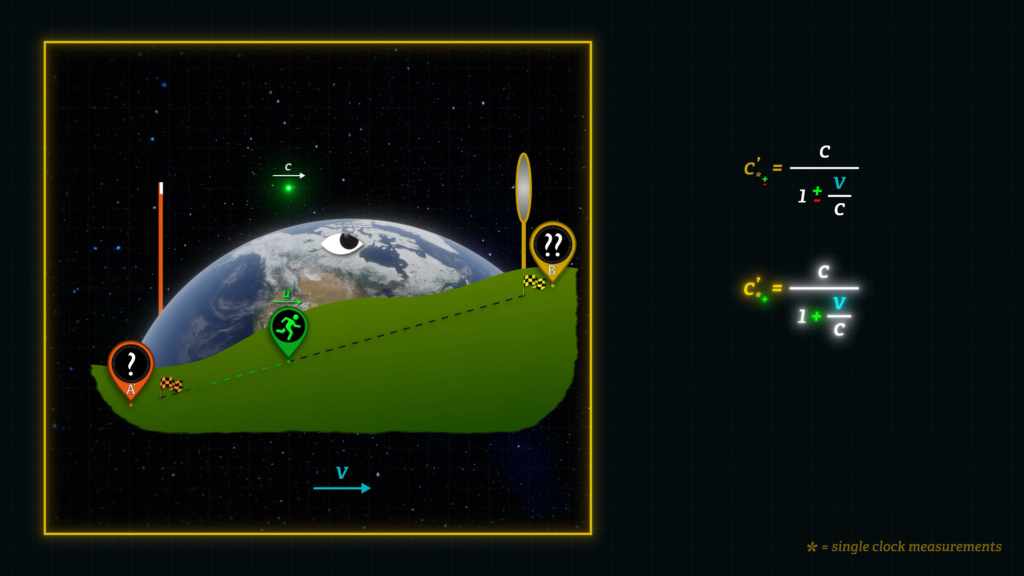
↓↓ \(\color{#e97031}{c_{* +}^{‘} = \frac{c}{1 + \frac{v}{c}}} \) ↓↓
And when light travels in the minus direction it will appear to travel faster than c in the Earth-frame or the moving Sagnac frame, when traveling opposite to the direction of reference frame motion.
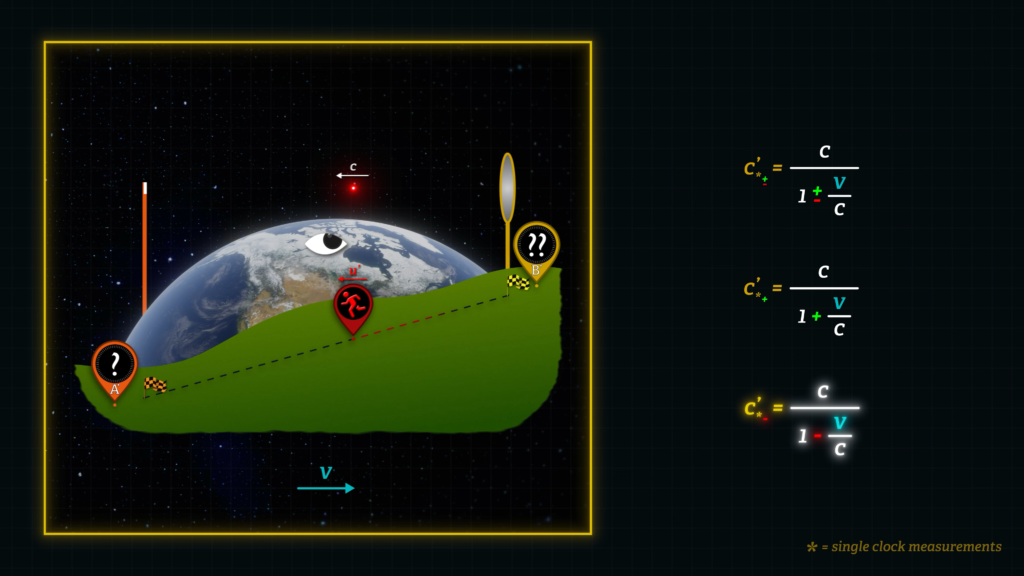
↑↑ \(\color{#e97031}{c_{* -}^{‘} = \frac{c}{1 – \frac{v}{c}}} \) ↑↑
In other words, if we could actually measure one-way light speeds, the difference between those two speeds might actually allow us to predict the speed of the Earth through space or the speed at which Sagnac device is moving.
Now, it’s very interesting to note why the time-weighted average of two-way light speed on the Earth is equal to c.
\(c_{twa}^{‘} = \frac{\color{#e97031}{c_{* +}^{‘}}\color{#34749d}{dt_{* +}^{‘}} + \color{#e97031}{c_{* -}^{‘}}\color{#34749d}{dt_{* -}^{‘}}}{\color{#34749d}{dt_{* +}^{‘}} + \color{#34749d}{dt_{* -}^{‘}}} \)
\(c_{t w a}^{\prime}=\frac{\frac{\color{#e97031}{c}}{\color{#e97031}{\left(1+\frac{v}{c}\right)}} \cdot \frac{\color{#34749d}{d x^{\prime}}}{\color{#34749d}{\gamma_L^2(c-v)}}+\frac{\color{#e97031}{c}}{\color{#e97031}{\left(1-\frac{v}{c}\right)}} \cdot \frac{\color{#34749d}{d x^{\prime}}}{\color{#34749d}{\gamma_L^2(c+v)}}}{\frac{\color{#34749d}{d x^{\prime}}}{\color{#34749d}{\gamma_L^2(c-v)}}+\frac{\color{#34749d}{d x^{\prime}}}{\color{#34749d}{\gamma_L^2(c+v)}}}\)
\(c_{twa}^{‘} = c \)
When we multiply speed in the positive direction by elapsed time in the positive direction, and add it to speed in the negative direction multiplied by elapsed time in the negative direction, and divide that sum by total elapsed time, we always get speed c.
This is why experiments that measure two-way light speed always yield a value of c.
This is true even when electric fields are used to transmit signals over part of the round-trip path. Scientists who think they have measured one-way time-of-flight almost always measure two-way information transfer, because we must include the transmission of electric field information as part of the information loop. This is why experiments to measure the speed of light always produce a speed of c, even if light is traveling at speed c’-star-plus in one direction and c’-star-minus on the return trip.
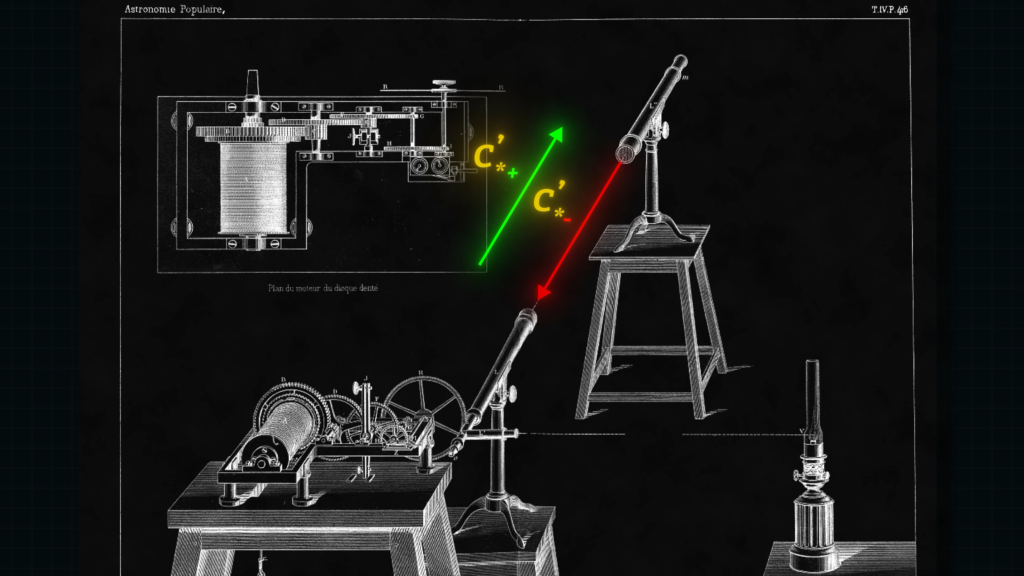
But a Sagnac device is unique, it does not measure 2-way light speed.

This is analogous to saying that we will approach a speeding vehicle from behind at a slower relative speed than if we crush into a similar vehicle in a head-on collision.


If we assume for the moment that the laboratory containing the Sagnac device is “stationary”, even though we know it is moving together with the Earth, we can work out the math to prove that it will reveal the one-way speed of light relative to the motion of the device.
Now I just have to say that scientists tried to discount the results of Sagnac’s experiment for many years, claiming that the rotation of the experimental apparatus disqualified it from being considered an inertial reference frame.
But in 2004 Wang, Zheng and Yao published a follow-on experiment in Physical Review Letters to remove these objections. They basically showed that light traveled at different speeds relative to the moving, linear portions of their device. And their results are consistent with the following formulas.

We can predict their results by removing the rightmost terms of the Lorentz Frame S’ time transform,
\(d t_{+}^{\prime}=\frac{d t_{+}}{\gamma_L}-\color{#ea3324}{\frac{v d x^{\prime}}{c^2}} \)
such that dt'(+) becomes,
\(dt_{\ast +}^{\prime}=\frac{dt_{+}}{\gamma_L} \)
dt (+) over the Lorentz gamma factor, and,
\(d t_{-}^{\prime}=\frac{d t_{-}}{\gamma_L}+\color{#ea3324}{\frac{v d x^{\prime}}{c^2}} \)
dt’ (-) becomes,
\(dt_{\ast -}^{\prime}=\frac{dt_{-}}{\gamma_L} \)
dt (-) over the Lorentz gamma factor.
This modification was proposed by Frank Tangherlini in 1961. The resulting formulas are called the Tangherlini transforms. They are similar to Lorentz transforms without Einstein’s clock adjustments and they work for experimental devices where the light signal travels in only one direction relative to the moving frame of the device, like a Sagnac device.
\(dx_{\pm} = \frac{dx^{‘}}{\gamma_{L}} \pm \frac{vdx^{‘}}{\gamma_{L}(c \mp v)} \)
\(dt_{\pm} = \frac{dx^{‘}}{\gamma_{L}(c \mp v)} \)
\(d x_{ \pm}^{\prime}=\gamma_L d x_{ \pm} \mp \gamma_L v d t_{ \pm} \)
\(dt_{* \pm}^{‘} = \frac{dt_{\pm}}{\gamma_{L}} = \frac{dx^{‘}}{\gamma_{L}^{2}(c \mp v)} \)
The Tangherlini transforms work perfectly to describe the Sagnac result, whereas the Lorentz transforms are inappropriate for measurements of one-way Frame S’ light speed in a Sagnac experiment. The bottom line is that a linear, one-way Sagnac experiment proves that light travels at different speeds relative to a moving inertial reference frame. The results of a Sagnac experiment disprove Einstein’s postulate that light travels at a constant speed relative to all inertial observers.
So, we’ve established the reality of different upstream and downstream light speeds when such speeds are measured with a single clock in a moving frame, such as in a Sagnac experiment. In other words, light does not always travel at speed c over a one-way path. That’s huge! And the established physics community simply does not want to admit it. With that attitude they’ll soon be less trusted than the legacy media.
Ok, we now need to take into consideration the refraction of light so that we can apply our theory to devices incorporating a refractive medium, such as a Fizeau water tube device.
Recall from Episode 9.3 that Max von Laue proposed that light would travel through a refractive medium at a constant speed relative to the medium, regardless of whether the medium was stationary or moving. Einstein further supported this notion, claiming that the assumption is validated by his principle of relativity.
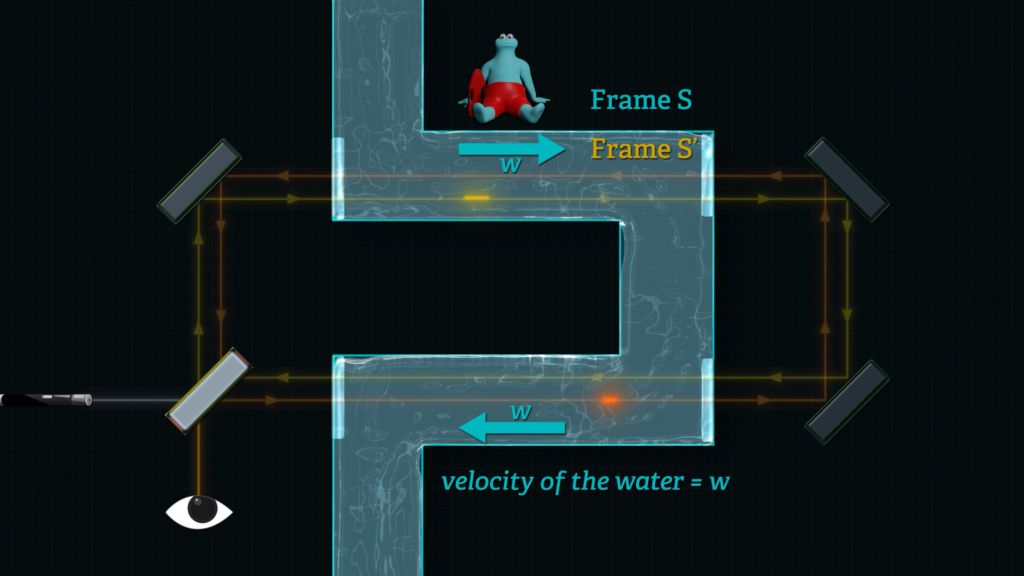
Well, they unknowingly were referring to the time-weighted average of two-way light speed through refractive media, not the one-way speed measured with a Sagnac device.
Von Laue concluded that light passing through a moving, refractive medium would travel at what we call speed c’-sub-twa divided by the refractive index of the medium, n.
\(u_x^{\prime}=\frac{d x^{\prime}}{d t_{\text {average }}^{\prime}} \quad u_x^{\prime}=\frac{c_{t w a}^{\prime}}{n} \quad c_{t w a}^{\prime}=c \)
Where the time-weighted-average, c’-sub-twa, is the two-way, round-trip speed of light, which we know numerically is always speed c.
\(u_x^{\prime}=\frac{d x^{\prime}}{d t_{\text {average }}^{\prime}} \quad u_x^{\prime}=\frac{c_{t w a}^{\prime}}{n}=\frac{c}{n} \quad c_{t w a}^{\prime}=c \)
\(\frac{d x^{\prime}}{d t_{\text {average }}^{\prime}}=\frac{c_{t w a}^{\prime}}{n} \)
From this we can derive the average value for dt’ for a refractive medium: n times dx’ divided by c’-sub-twa.
\(d t_{\text {average }}^{\prime}=\frac{n d x^{\prime}}{c_{t w a}^{\prime}} \)
Now we’re allowed to use the Lorentz transforms in the stationary frame even when there’s only one clock. So, if we use this average value of dt’ in a Lorentz dt-transform, we get a formula that solves for dt (±) in a refractive medium.
\(d t_{n \pm}=\gamma_L d t_{a v e r a g e}^{\prime} \pm \gamma_L \frac{v d x^{\prime}}{c^2} \)
\(d t_{n \pm}=\gamma_L \frac{n d x^{\prime}}{c_{t w a}^{\prime}} \pm \gamma_L \frac{v d x^{\prime}}{c^2} \)
\(d t_{n \pm}=\gamma_L \frac{d x^{\prime}}{c_{t w a}^{\prime}}\left(n \pm \frac{v}{c}\right) \)
And this allows us to compute one-way light speed through a refractive medium as measured with a single clock in a stationary frame.
\(c_{*n\pm}^{\prime}=\frac{\gamma_L dx^{\prime}}{dt_{n \pm}} \)
\(c_{*n\pm}^{\prime}=\frac{\gamma_L dx^{\prime}}{\gamma_L \frac{dx^{\prime}}{c_{twa}^{\prime}}\left(n \pm \frac{v}{c}\right)} \)
We see that light speeds in the moving frame of a refractive medium are equal to time-weighted-average speed c divided by the refractive index plus or minus v over c.
\(c_{\ast n\pm}^{\prime}=\frac{c_{twa}^{\prime}}{n \pm \frac{v}{c}} \)
That’s right, light also travels at different one-way speeds when a refractive medium is moving relative to a stationary reference frame.
We are now armed with the fundamentals that we will need in order to begin to understand how the passage of light through a refractive medium differs in a Fizeau versus a Sagnac experiment, and how this difference will give us insight into how light interacts with a refractive substance.
OK, that’s it for now. If you have any questions, please write them in the comments section. And if I’ve caused you to think outside the box, please rate this video favorably. I’m Joe Sorge, and thanks for watching.



