Welcome to Ask Us Whatever. I’m Joe Sorge.
In Episode 7.1, I pointed out that if Clock A is ticking slower than Clock B, then it’s impossible for Clock A to also be ticking faster than Clock B in the same setup.
I received a nice comment from Jonathan Doolin who pointed out that Herbert Dingle made similar arguments in the 1960s and 1970s, but after the journal Nature received rebuttals to Dingle’s arguments, the journal subsequently censored Dingle by not allowing him to publish anything more on the subject. Jonathan kindly pointed me to a 2022 Researchgate article of his own, a link to which we have put on the askuswhatever.com web site, explaining why Dingle’s argument was rejected.
So, this episode will focus on whether Dingle was wrong, whether I was wrong, or whether there is a way to reconcile the different positions of Dingle, Einstein, Doolin, and myself.
Prior to getting into the details, the answer is that one must distinguish between a clock’s tick rate and the impact of Einstein clock synchronization on its time reading. Dingle and I were talking about tick rates. I am certain that Einstein did not believe that one could simply snap one’s fingers and cause the tick rates of clocks to change, or that the tick rates of clocks would somehow telepathically respond to each observers’ mental perceptions of relative motion. Anyone who believes that this is how Special Relativity works, doesn’t understand it. You can certainly have one frame moving relative to another frame, but you cannot create a setup in which the clocks of one frame are dilated and offset differently, and then just wave a magic wand and assume that the time dilations and clock offsets will magically flip so that you can use the inverse Lorentz transformation to solve a problem on a physics exam.
As we learned in the prior two episodes, Einstein used his unique clock synchronization method to alter the readings of clocks, based on their physical location. The method either “adjusts forward” or “adjusts backwards” the time reported by clocks based on their location along the axis of reference frame motion. His method creates a spatial gradient of clock readings in the direction of motion. In this episode we’ll show how Einstein clock synchronization can create the illusion that less time passes in an another inertial reference frame.
Let’s bring back a couple of the characters from Episode 7.2. Our snarky clown is on a spaceship, which let’s say is in Frame \(S^\prime \), moving at speed \(v \) relative to what we jokingly called the cosmic train station, which resides in Frame \(S \). Our playful Master of the Universe observes the clown’s spaceship from the perspective of the cosmic train station, and vice versa.
We will call the taking of a reading from a clock an “event”. The question that we will ask is whether the Clown will perceive the clocks in Frame \(S \) to record less time between certain events than the clocks in Frame \(S^\prime \); while the Master will perceive the clocks in Frame \(S^\prime \) to record less time between the same events than the clocks in Frame \(S \).
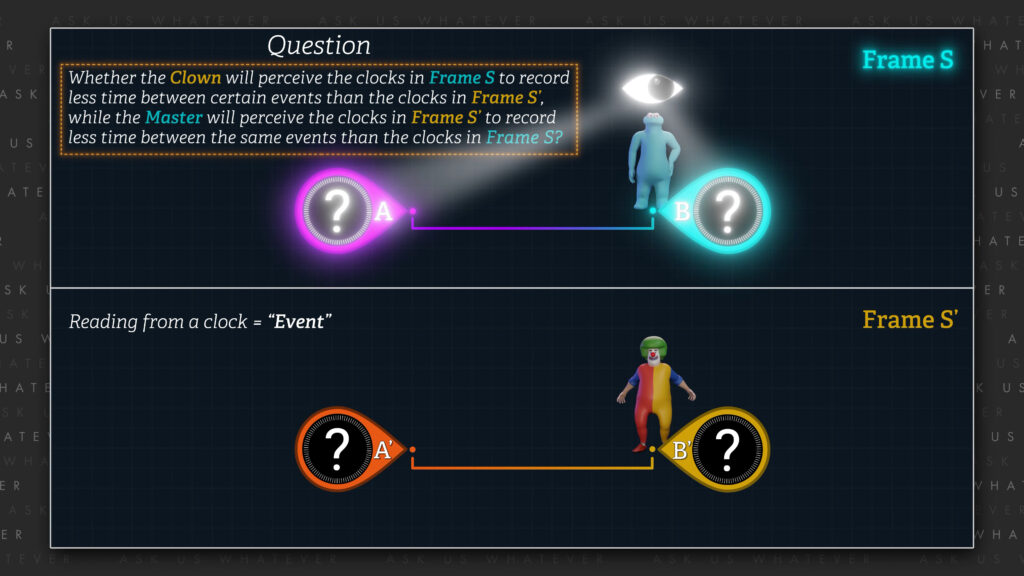
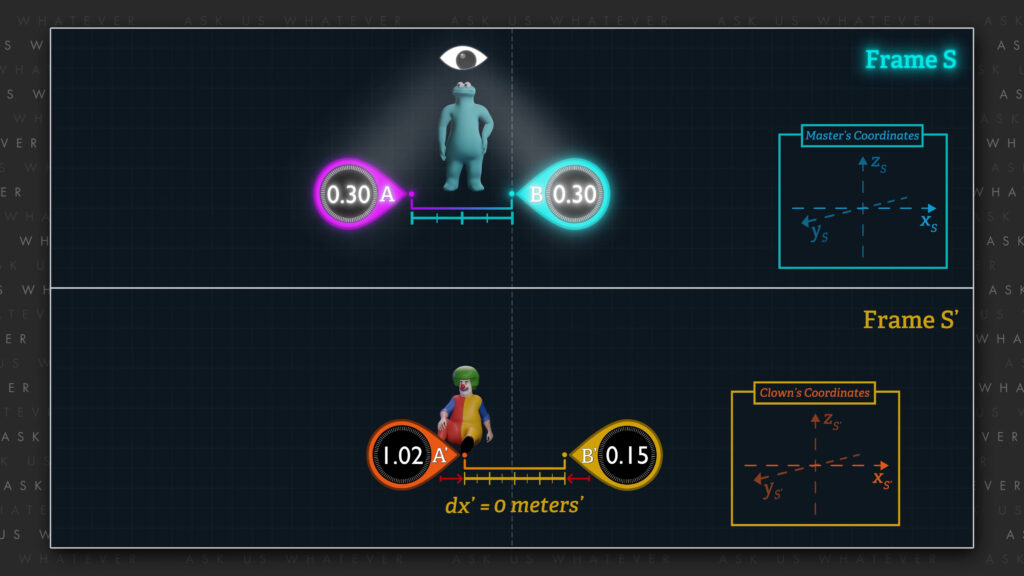
Recall that the Clown helped to synchronize the spaceship clocks \(A \) and \(B \) in Episode 7.2. We will now rename these clocks \(A^\prime \) and \(B^\prime \) to signify that they and the Clown are in Frame \(S^\prime \). In Episode 7.2, the spaceship clocks were separated by a distance of 1 light-second\(^\prime \) (about 300 million meters\(^\prime \)). We will call the distance that the Clown’s position changes while taking readings at clocks \(A^\prime \) and/or \(B^\prime \): \(dx^\prime \) If the clown’s position does not change within Frame \(S^\prime \) and the clown takes readings from only one clock within Frame \(S^\prime \), then \(dx^\prime \) will be zero, even if clocks \(A^\prime \) and \(B^\prime \) remain one light-second’ apart.
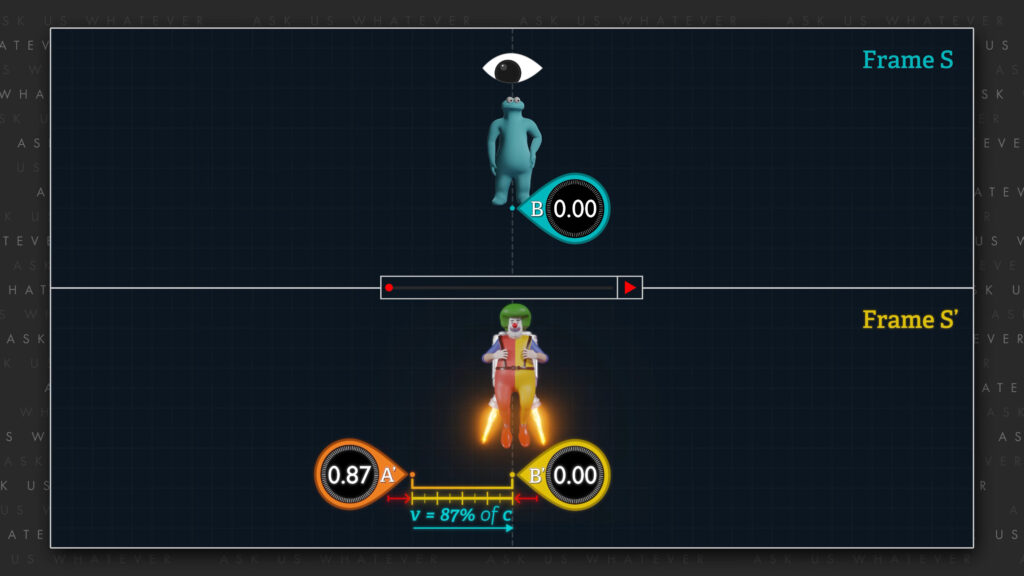
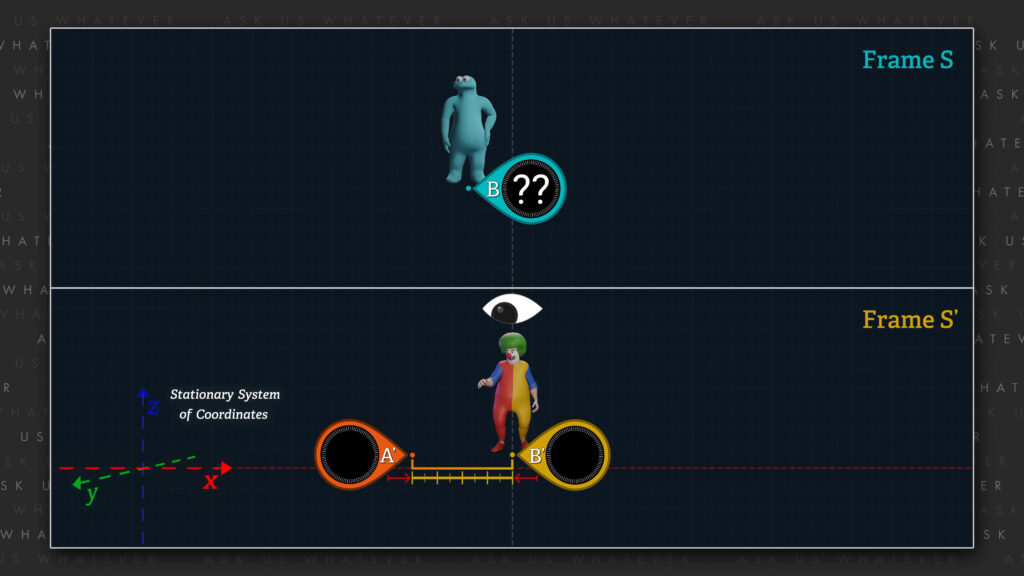
We assumed in Episode 7.2 that Frames \(S \) and \(S^\prime \) move relative to each other at about 87% of speed \(c \). We illustrate that here with Frame \(S^\prime \) moving in the positive x-direction at about 87% of speed \(c \) relative to the stationary Frame \(S \). Einstein’s theory requires us to establish what he called “a stationary system of coordinates” (that is, x, y, and z axes that he deemed to be stationary in “space”), and to deem one of the two reference frames as having zero speed with respect to that stationary system of coordinates. In other words, we cannot have one frame moving at speed \(v \) relative to the x-axis of the stationary system of coordinates while the other frame moves at speed \(v \) in the negative x-direction with respect to the same stationary system of coordinates. In that case, the reference frames would not be moving at speed \(v \) relative to each other.
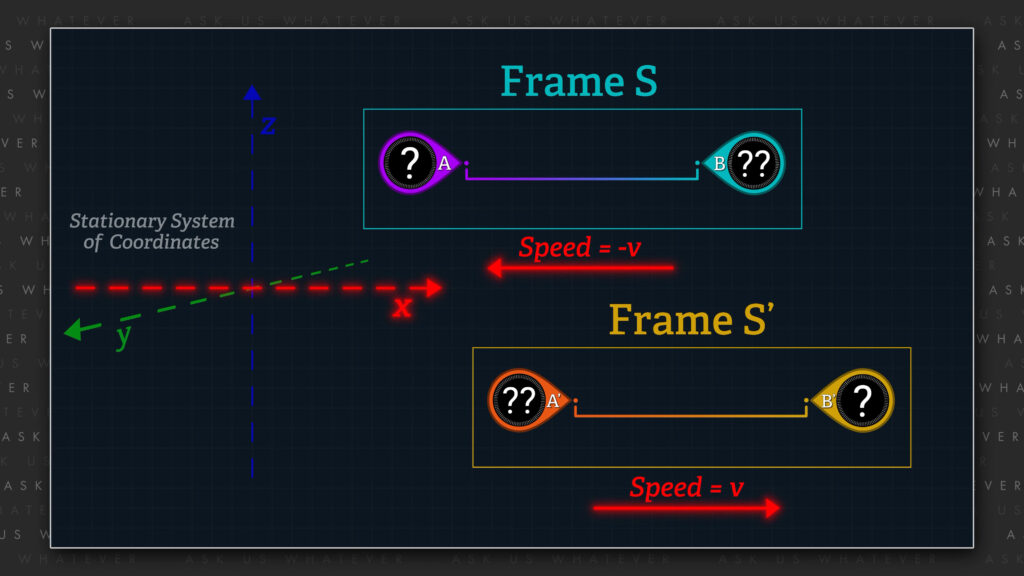
We must assign a zero speed to one of the reference frames; which I believe causes Special Relativity to be deeply rooted in the concept of a universal, preferred frame in which there is no offset between its clocks. But that’s a debate for another day.
The symbol \(dx \) will represent the distance traveled, if any, by the Master when taking clock readings in Frame \(S \), as measured in Frame \(S \) meters. In our initial scenario, we will assume that the Master and Frame \(S \) do not move with respect to the cosmic train station, and that the Master stands beside clock \(B \) When the Master is stationary in Frame \(S \), the Master uses only one Frame \(S \) clock to measure time, and \(dx \) is equal to zero.
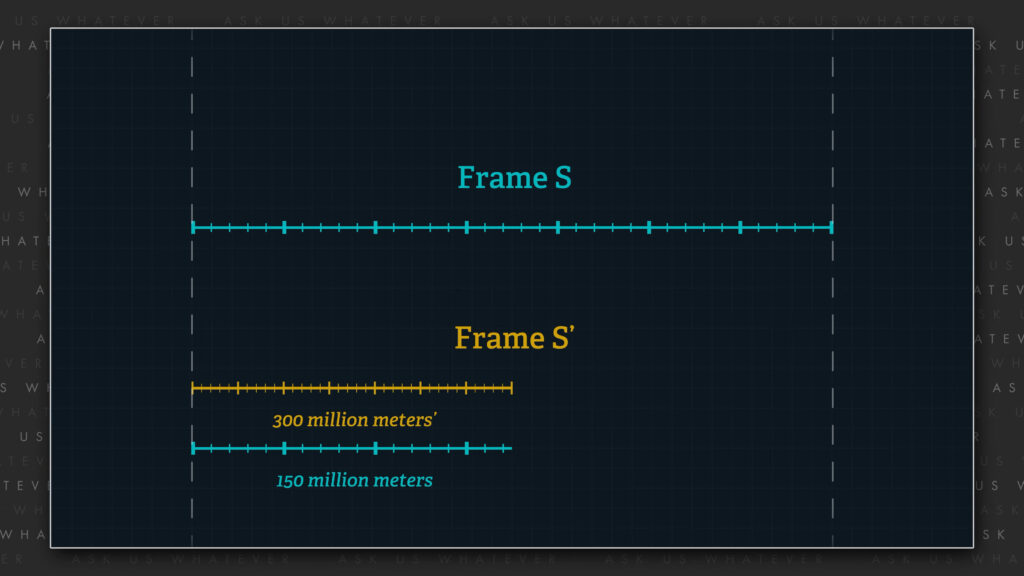
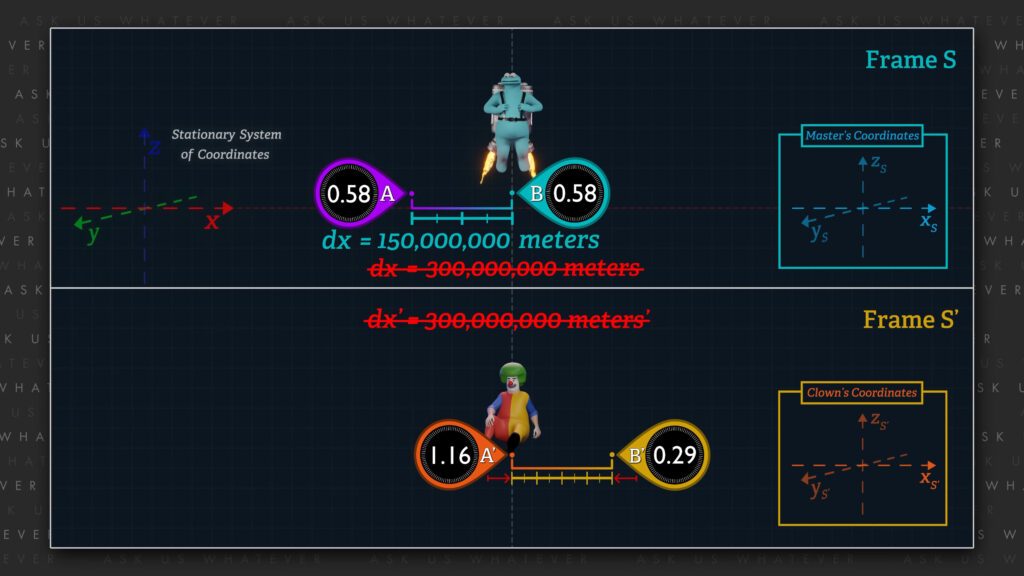
Now, Special Relativity assumes that an observer in the stationary frame will perceive the length of objects in the moving frame to contract by the Lorentz gamma factor. So, from the perspective of Frame \(S \), the objects within Frame \(S^\prime \) will contract. And at about 87% of speed \(c \), Frame \(S^\prime \) will appear to contract by about a factor of 2.
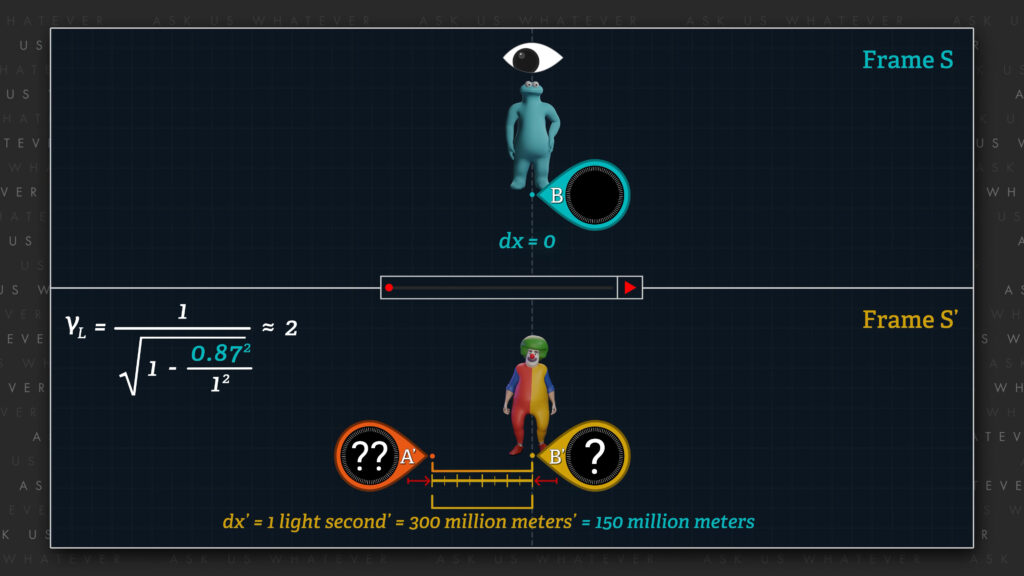
So, if, the \(S^\prime \) clocks are separated by a distance equal to 1 light-second\(^\prime \) (or about 300 million meters\(^\prime \)), observers in Frame \(S \) will observe the clocks to be separated by about a 150 million uncontracted, non-primed meters. To be clear, at this relative speed, meter\(^\prime \)-sticks in Frame \(S^\prime \) will be about half the length of the meter-sticks of Frame \(S \), and so 300 million meter\(^\prime \)-sticks lined up end to end would be comparable to 150 million meter-sticks lined up similarly.
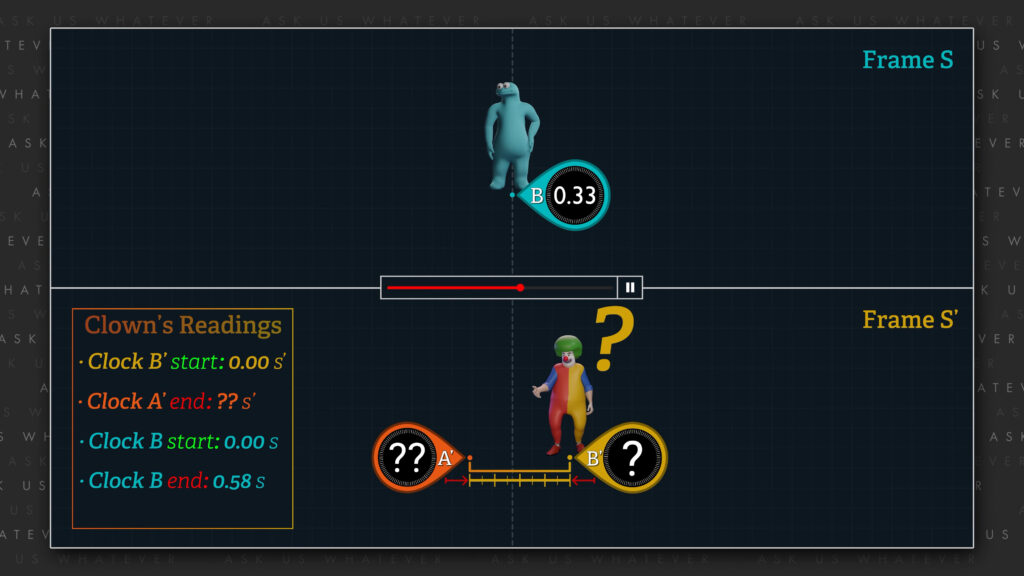
In our first scenario, we will assume that the Clown takes a reading at clock \(B^\prime \) when clock \(B^\prime \) is aligned with clock \(B \), and then takes a reading at clock \(A^\prime \) when clock \(A^\prime \) becomes aligned with clock \(B \). The two clock readings will be separated in Frame \(S^\prime \) by 300 million meters\(^\prime \) in the negative x-direction.
In order to calculate \(dt \), which is the time that elapses in Frame \(S \) while Frame \(S^\prime \) moves such that the alignment of clock \(B \) (and the Master) change from being aligned with clock \(B^\prime \) to being aligned with clock \(A^\prime \), we take \(dx^\prime \) divided by gamma (which is now the length-contracted distance between clocks \(A^\prime \) and \(B^\prime \) as measured from Frame \(S \)), and divide by the speed, \(v \), of the \(S^\prime \) Frame relative to Frame \(S \). We get \(dt \) equals 300 million meters\(^\prime \) divided by a gamma factor of 2 meters\(^\prime \) per meter times 1 over 261 million meters per second. This produces a time of about 0.58 seconds.
\(dt\ on\ clock\ B=\frac{\left|dx^\prime\right|}{\gamma}\times\frac{1}{v} \)
\(dt\ on\ clock\ B=\frac{\left|dx^\prime\right|}{\gamma}\times\frac{1}{0.87c} \)
\(dt\ on\ clock\ B=\frac{\left|-300\ million\ meters^\prime\right|}{2meters^\prime/meter}\times\frac{1\ }{261\ million\ meters/second} \)
\(dt\ on\ clock\ B\approx\frac{1.15}{2}\ s\approx0.58\ s \)
Clock \(B \) will show that about 0.58 seconds elapse from being aligned with clock \(B^\prime \) to being aligned with clock \(A^\prime \), because 1/2 light-second\(^\prime \) traversed at 87% of \(c \) will require about 0.58 seconds.
Let’s confirm this result with a Lorentz transformation. When dx is zero, gamma is 2, v is 261 million meters per second, and, as we just calculated, \(dt \) is 0.58 seconds, \(dx^\prime \) equals 2 times zero minus 2 meters\(^\prime \) per meter times 261 million meters per second times 0.58 seconds.
\(dx^\prime=\gamma_Ldx-\gamma_Lvdt \)
\(dx^\prime\approx2\times0-2\frac{meters^\prime}{meter}\times261,000,000\frac{meters}{second}\times0.58\ seconds \)
\(dx^\prime\approx-300,000,000\ meters^\prime \)
We get about negative 300 million meters\(^\prime \) (about 1 light-second\(^\prime \)) as predicted. The value is negative because the Clown moved in the negative x-direction within Frame \(S^\prime \) between taking the first clock reading at clock \(B^\prime \) and taking the second clock reading at clock \(A^\prime \). This implies that the Clown will compute the value of \(dt^\prime \) using readings from both clocks \(A^\prime \) and \(B^\prime \).
Let’s think about it: if the Clown remained at the location of clock \(B^\prime \) while Frame \(S^\prime \) moved, the Clown would not know when clock \(A^\prime \) became aligned with clock \(B \). Afterall, clocks \(A^\prime \) and \(B^\prime \) are 300 million meters\(^\prime \) apart in the Clown’s Frame. So, the Clown would not be able to measure the time elapsed during the interval starting with clock \(B^\prime \) being aligned with clock \(B \) and ending with clock \(A^\prime \) being aligned with clock \(B \).
However, if the Clown were to strap on a rocket pack and hover in space while clocks \(B^\prime \) and \(A^\prime \)were to whiz by, the Clown could observe the difference in readings reported between clocks \(B^\prime \) and \(A^\prime \).

So, can we predict the difference in readings between clocks \(B^\prime \) and \(A^\prime \) observed by the clown? Yes! We can do it in two ways. The first approach is by using the Lorentz dt’ transformation.
\(dt^\prime=\gamma_Ldt-\gamma_L\frac{vdx}{c^2}\ \ \ \ \ \ \ \ dx=0 \)
\(dt^\prime=2\times0.58-2\frac{0.87\times0}{1^2} \)
\(dt^\prime=2\times0.58\approx1.16\ seconds^\prime \)
Gamma times \(dt \) minus gamma times \(v \) times \(dx \) over \(c \) squared. Since \(dx \) is zero in our first scenario, \(dt^\prime \) is simply 2 times \(dt \), or about 1.16 seconds\(^\prime \).
But the Lorentz \(dt^\prime \) transformation formula doesn’t really give us a very good insight into what’s actually happening, and it requires us to ignore some convoluted unit analysis challenges.
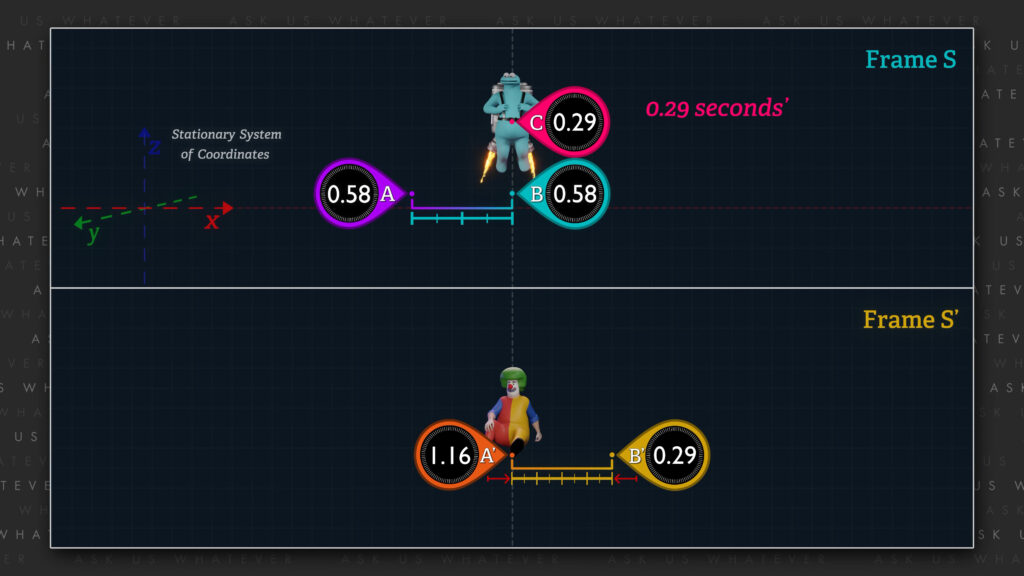
A more intuitive approach is to use what we learned about the spatial gradient of clock offsets in Episodes 7.1 and 7.2. We learned that, from the perspective of Frame \(S \), the reading on clock \(A \) will be ahead of clock \(B^\prime \) by about 0.87 seconds\(^\prime \) due to Einstein’s clock synchronization protocol (see Episode 7.2 if that’s not clear). And so, when clock \(B^\prime \) is aligned with clock \(B \), clock \(B^\prime \) will report a reading of zero, and clock \(A^\prime \) will report a reading of 0.87 seconds\(^\prime \)
We can also say that since Frame \(S^\prime \) moves at 87% of speed \(c \) relative to Frame \(S \), the tick rate of clocks in Frame \(S^\prime \) will be slower than the tick rate of the clocks in Frame \(S \) by the Lorentz gamma factor, which, at 87% of \(c \), is about a factor of 2 slower. So instead of reporting an elapsed time of 0.58 Frame \(S \) seconds, as reported by the clocks in Frame \(S \), the clocks in Frame \(S^\prime \) will each report an elapsed time of about half that, or about 0.29 seconds\(^\prime \). This means that clock \(A^\prime \) will advance from an initial reading of 0.87 seconds\(^\prime \) to a final reading of 1.16 seconds\(^\prime \). And clock \(B^\prime \) will advance from an initial reading of zero to a final reading of 0.29 seconds\(^\prime \).
So, if the Clown hovers in space, and compares the reading on clock \(B^\prime \) at the beginning of these events (a reading of zero) to the reading on clock \(A^\prime \) at the end of these events (a reading of 1.16 seconds\(^\prime \)) the Clown will be led to believe, erroneously, that 1.16 seconds\(^\prime \) elapsed in Frame \(S^\prime \) during the interval beginning with clock \(B \) aligning with clock \(B^\prime \) to clock \(B \) aligning with clock \(A^\prime \).
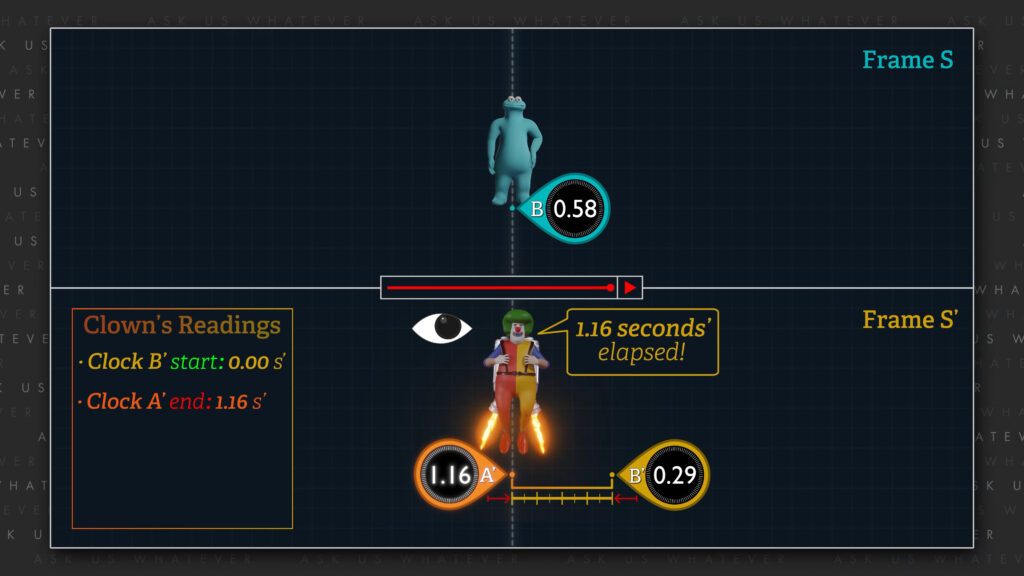
This 1.16 seconds\(^\prime \) is in perfect agreement with a rearranged version of the Lorentz transformation for time \(dt^\prime \).
\(dt^\prime=\frac{dt}{\gamma_L}-\frac{v\left(-dx^\prime\right)}{c^2} \)
In other words, the Lorentz transformation for time \(dt^\prime \) does not merely compute the time elapsed on a single clock in Frame \(S^\prime \). The Lorentz formula for \(dt^\prime \) also adjusts the value of \(dt^\prime \) by the spatial gradient of clock readings between clocks \(A^\prime \) and \(B^\prime \); or in other words, by the clock offset between clocks \(A^\prime \) and \(B^\prime \) caused by the synchronization of these clocks using Einstein’s protocol.
So, what do the Clown and the Master observe in the first scenario?
Well, the Master and the Clown are able to observe that 0.58 seconds elapse on a single clock in Frame S, while the clown observes that clocks \(B^\prime \) and \(A^\prime \) differ by 1.16 seconds’ if clock \(B^\prime \) is read when it is aligned with clock B and then clock \(A^\prime \) is read when it becomes aligned with clock B.
Since the Clown was able to look over at clock \(B \) when clock \(B \) was aligned with clock \(B^\prime \), and also later when clock \(B \) was aligned with clock \(A^\prime \), the Clown would have noticed that 0.58 seconds had elapsed on clock \(B \) in that interval.
And so, the Clown would have concluded that half as many seconds elapsed in Frame \(S \) (0.58 seconds) as compared to the number of seconds\(^\prime \) (1.16 seconds\(^\prime \)) that the Clown was led to believe had elapsed in Frame \(S^\prime \).
Let’s now confirm the Clown’s observation of 0.58 seconds using the Lorentz transformation for \(dt \), which is gamma times \(dt^\prime \) plus gamma times \(v \) times \(dx^\prime \) over \(c \)-squared. The numerical value is about 0.58 seconds, which is the Frame \(S \) time we computed earlier. So far, our analysis is consistent with commonly held beliefs about Special Relativity.
\(dt=\gamma_Ldt^\prime+\gamma_L\frac{vdx^\prime}{c^2} \)
\(dt\approx2\frac{seconds}{second^\prime}\times1.16seconds^\prime \)
\(+\ 2\ meters/meter^\prime \times \ 261,000,000\ meters/second \)
\(\times \ \frac{-300,000,000\ meters^\prime}{{300,000,000}^2\frac{meters^2}{second^2}} \)
\(dt\approx0.58\ seconds \)
But what if the Master had noted the time on clock \(B^\prime \) when clock \(B^\prime \) was aligned with clock \(B \), and then later noted the time on clock \(A^\prime \) when clock \(A^\prime \) became aligned with clock \(B \)? Oops, the Master would observe a time difference of 1.16 seconds\(^\prime \) in Frame \(S^\prime \). And during that same interval, the Master would observe only about 0.58 seconds to elapse on clock \(B \).
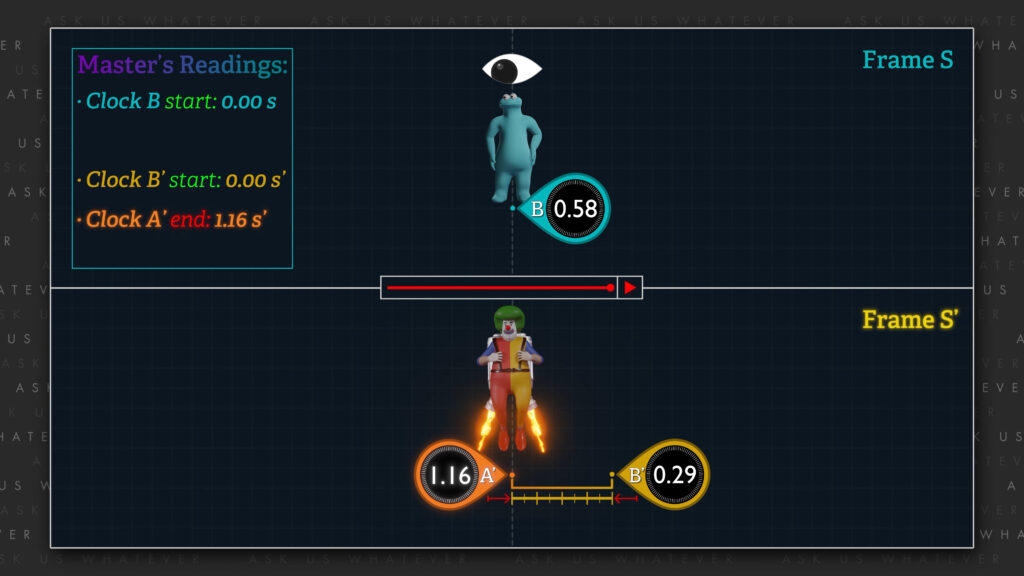
Thus, the Master would conclude that twice as much time had elapsed in the Clown’s Frame \(S^\prime \) as compared to the Master’s own Frame \(S \). This is the opposite of what we’re told should happen in Special Relativity.
This is an inconvenient truth for the commonly held beliefs about Special Relativity, but not one that is ever discussed.
Alright, let’s poke the tiger a little more.
The Clown didn’t tell anyone, but just to be safe the Clown took a personal clock on the rocket pack journey as well.

And guess how much time elapsed on the Clown’s personal clock? The same amount of time as had passed on the Frame \(S \) clock! The Clown’s speed relative to Frame \(S \) was zero, and so the Clown’s personal clock ticked at the same rate as the clock in Frame \(S \). 0.58 seconds elapsed on the Clown’s personal clock, not 1.16 seconds.

So which clock and which observer’s perspective is the one that counts? Well that depends on whether you want to believe in the myths of Special Relativity or not.
Special Relativity and the Lorentz transformations direct the Clown to compare the time readings on the two clocks in Frame \(S^\prime \) and then compare that presumed elapsed time to the readings of a single-clock in Frame \(S \), ignoring the Clown’s own personal clock. What’s more, the Clown cannot tell the Master how much time the Clown believes had elapsed in Frame \(S^\prime \), and the Master cannot look at the clocks in Frame \(S^\prime \), otherwise the Master would be led to believe that more (not less) time elapsed in Frame \(S^\prime \)!
Special Relativity restricts information and constrains observations to steer the narrative. It’s like Facebook!
Okay! Well, that was fun, so let’s poke the tiger some more.
Defenders of Special Relativity claim that both observers will observe less time to elapse in the opposite frame. Let’s find out what the observers need to do to make this work.
There’s a common misperception that the formula symmetry that exists between the two sets of Lorentz transformations represents reference frame symmetry.
\(x=\gamma_Ldx^\prime+\gamma_Lvdt^\prime \)
\(dt=\gamma_Ldt^\prime+\gamma_L\frac{vdx^\prime}{c^2} \)
\(dx^\prime=\gamma_Ldx-\gamma_Lvdt \)
\(dt^\prime=\gamma_Ldt-\gamma_L\frac{vdx}{c^2} \)
In other words, that the second two equations represent a relativistic symmetry when events are observed from Frame \(S^\prime \) instead of being observed from Frame \(S \). And that this perceived symmetry somehow causes the clocks in the opposite frame to change their tempo through the powers of mental perception.
Einstein contributed to some of the confusion when he stated, in his 1907 paper on Special Relativity:
If one solves the [transformation] equations with respect to x, y, z, t, one obtains the same equations, except that the “primed” quantities are replaced by the corresponding “unprimed” quantities-and conversely, and \(v \) is replaced by \(-v \). This also follows directly from the principle of relativity…
This statement is more complicated than it first seems. What does it mean when we “replace” the “primed” quantities with the “unprimed” quantities, and vice versa?
Well, since Einstein references the principle of relativity, he is describing a reversal of perspectives.
In other words, from the perspective of observers in Frame \(S^\prime \), it will appear that Frame \(S \) is moving. He is effectively re-anchoring the stationary system of coordinates to Frame \(S^\prime \) instead of Frame \(S \), and then measuring Frame \(S \) motion relative to it.
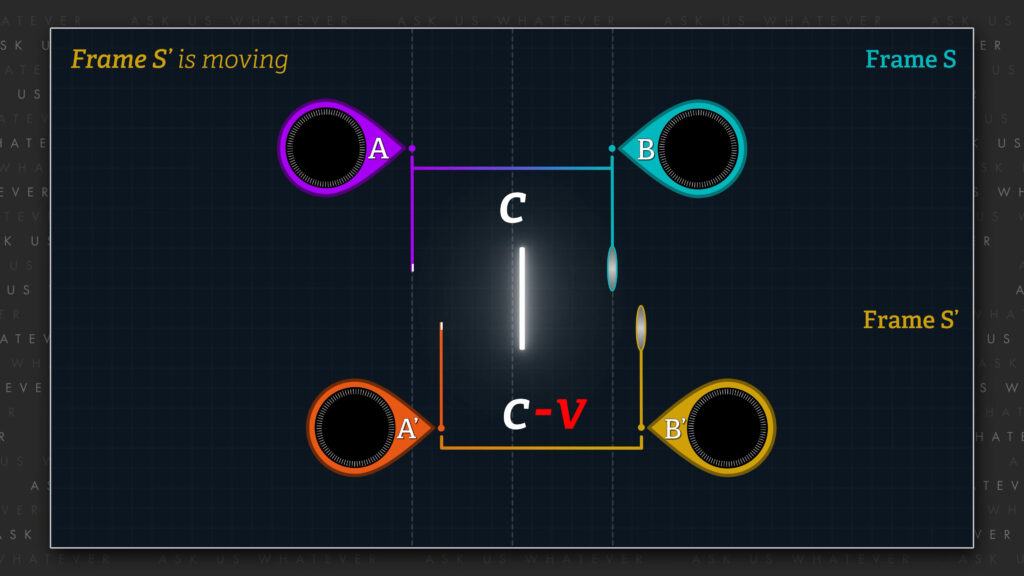
So, let’s carry out a simple numerical swap of distance and time values and also reverse the polarity of \(v \). The Lorentz transformations yield… A perfect numerical symmetry! Which is what one would expect since the formulas themselves are symmetric. Very nice. But what does it mean to the setup and to the real world?
\(dx=\gamma_Ldx^\prime+\gamma_Lvdt^\prime=2\times0+2\times\left(-260\right)\times0.58\approx-300\ million\ meters \)
\(dt=\gamma_Ldt^\prime+\gamma_L\frac{vdx^\prime}{c^2}=2\times0.58+2\times\left(-260\right)\times\frac{0}{{300}^2}\approx1.16\ seconds \)
\(dx^\prime=\gamma_Ldx-\gamma_Lvdt=2\times\left(-300\right)-2\times\left(-260\right)\times1.16=0\ meters^\prime \)
\(dt^\prime=\gamma_Ldt-\gamma_L\frac{vdx}{c^2}=2\times1.16-2\times\left(-260\right)\times\frac{-300}{{300}^2}\approx0.58\ seconds^\prime \)
Let’s start by looking at the formula for \(dx \). We’ve substituted the new values for \(dx^\prime \), \(v \), and \(dt^\prime \) into the formula, and sure enough it yields the new \(dx \) value of negative 300 million meters. As you might recall, negative 300 million meters\(^\prime \) was the original value for \(dx^\prime \). Now negative 300 million meters is the value for \(dx \). The same swapping of values works for the \(dx^\prime \) formula, and we get a new value of zero, which is the original value for \(dx \).
So, what does it mean to our setup that \(dx^\prime \) is now zero? It means that the Clown now does not move with respect to the \(x^\prime \) axis of Frame \(S^\prime \). Which means that the Clown now remains stationary beside only one clock in Frame \(S^\prime \).
And the new value of negative 300 million meters for \(dx\) means that the Master must move negative 300 million meters with respect to the x-axis of Frame \(S \). We’ll get to what that means to the setup after we examine \(dt \) and \(dt^\prime \).
The Lorentz formulas for dt and dt’ have swapped their inputs and outputs as well. We see that the Frame \(S \) clocks now yield a \(dt \) value of 1.16 seconds instead of the original value of 0.58 seconds.
Who of you thinks that is due time dilation? In the first setup Frame \(S \) was stationary and now Frame \(S \) is presumably moving. So, do moving clocks tick faster than stationary clocks? No! Obviously that line of reasoning leads to the letter F, in more ways than one. So, there must be a different explanation.
Let’s explore the meaning of changing the sign of \(v \) to negative \(v \).
Intuitively we think of this as now observing the setup from the perspective of the Clown in Frame \(S^\prime \) instead of from the original perspective of our playful Master of the Universe in Frame \(S \).
In his 1905 relativity paper, Einstein defined v using the phrase, “a uniform motion of parallel translation with velocity \(v \) along the axis of x in the direction of increasing x”.
In our original setup, the Master observed Frame \(S^\prime \) moving in the positive x-direction, relative to the x-axis of Frame \(S \).
But now, after we swap all of the values and change \(v \) to negative \(v \), the Clown remains stationary and Frame \(S \) moves in the negative x\(^\prime \)-direction. Speed \(v \) is now negative as viewed from the perspective of the Clown in Frame \(S^\prime \), and is measured in Frame \(S^\prime \) units of meters\(^\prime \) per second\(^\prime \).
Remember that speed \(v \) is the speed at which an observer measures another Frame to be moving using the axes and dimensional units of the observer’s Frame. So, \(v \) is now the speed that the Clown measures Frame \(S \) to be moving relative to the Clown’s x\(^\prime \) axis, as measured in units of meters\(^\prime \) per second\(^\prime \).
OK, here’s where Special Relativity plays a little fast and loose with the setup.
Originally the x-axis was pointing in the direction of Frame \(S^\prime \) motion, since \(v \)was originally positive. But now the Master must move negative 300 million meters with respect to the x-axis of Frame \(S \), since \(dx \) is negative 300 million meters. If the x-axis remains unchanged relative to the orientation of Frame \(S \), then the Master would have to race from clock \(B \) to clock \(A \) while Frame \(S \) moves in the negative x \(^\prime \)-direction. And as we will see, this will not produce the new value of 1.16 seconds for \(dt \).
As you may recall from our discussions of clock offset, if Frame \(S \) is now moving, the clocks in Frame \(S \) will need to be Einstein synchronized using a light signal as described in his 1905 paper and reviewed in our Episode 7.2.
Fortunately, the \(dt^\prime \) transformation shows us how the Frame \(S \) clocks must change. Let’s use some fast algebra to re-arrange the \(dt^\prime \) transformation to solve for \(dt \).
\(dt^\prime=\gamma_Ldt-\gamma_L\frac{vdx}{c^2} \)
\(dt^\prime+\gamma_L\frac{vdx}{c^2}=\gamma_Ldt \)
\(dt=\frac{dt^\prime}{\gamma_L}+\frac{vdx}{c^2} \)
We know that the new value of \(v \) is negative, and the new of \(dx \) is negative. So, the second term of the rewritten \(dt \) formula shows that we will be adding time to the first term, \(dt^\prime \) divided by gamma. In other words, Frame \(S^\prime \) is now stationary and so we have to divide \(dt^\prime \) by gamma to convert stationary Frame \(S^\prime \) seconds\(^\prime \) to moving Frame \(S \) seconds (it’s the reverse of what we’re used to because we have swapped values and perspectives). And then we must add \(v \) times \(dx \) over \(c \)-squared seconds when moving against the direction of Frame \(S \) motion. Why? Because now we have a clock-offset to consider in Frame \(S \). Why? Because Frame \(S \) is now moving at speed negative v and the Master is moving 300 million meters and reading from two clocks.
The second term of the rewritten \(dt \) formula shows us that the frame \(S \) clock offset is 0.866 seconds.
\(\frac{vdx}{c^2}=\left(-260,000,000\right)\times\frac{-300,000,000}{\left(300,000,000\right)^2} \)
\(=0.866\ seconds \)
And as always, the rear clock reports a time that is ahead of the front clock, so clock \(B \) will read 0.866 seconds when clock \(A \) reports zero. Which means that the Master must read clock \(A \) first and then read clock \(B \) second in order to pick up 0.866 seconds from the clock offset. Which means that the Master must move opposite to the direction of motion of Frame \(S \) (which, as you may recall, is what the Clown did in frame \(S^\prime \) in the original setup). Which means the Master will now move from left to right in our setup.
But doesn’t the x-axis point from left to right, in which case the Master will be moving positive 300 million meters instead of negative 300 million meters?
As I said earlier, this is another occasion where Special Relativity plays fast and loose with the setup.
The inverted Lorentz transformations require an inversion of the x-axis when \(v \) is swapped with negative \(v \). In other words, the x-axis now needs to point in the direction of Frame \(S \) motion so that the Master’s trip from clock \(A \) to clock \(B \) causes \(dt \) to gain time.
Awkwardly, Special Relativity does not dictate an inversion of the y or z axes.
According to Einstein’s 1907 paper, y = y\(^\prime \), not negative y\(^\prime \); and z = z\(^\prime \), not negative z\(^\prime \). So, by changing perspective from the Master to the Clown in our setup, while we would not expect an inversion of the z-axis, we should expect an inversion of both the y and the x-axes. Yet, Einstein does not change the sign of either the y or z values.
That’s an interesting contortion of the real world, don’t you think? There’s no universal logic to it, just expediency to attempt to create an imaginary symmetry. There are even more problems with Lorentz symmetry in the real world!
If Frame \(S \) is now moving and Frame \(S^\prime \) is now stationary with respect to the stationary system of coordinates, the lengths in Frame \(S \) must now contract by a factor of gamma and the lengths in Frame \(S^\prime \) now must expand by a factor of gamma.
Really? How and when did this happen? If Special Relativity describes the real world and not some fantasyland, what caused Frame \(S \) to suddenly contract? The repositioning of the stationary system of coordinates? The mental perceptions of the clown in Frame \(S^\prime \)? It’s silly, but without it the Lorentz math doesn’t work out. As I said, it’s a false symmetry.
Moreover, the clocks of Frame \(S \) will now need to beat at half their original rate, and the clocks of Frame \(S^\prime \) will need to beat at double their original rate. And the clock offsets that were originally in Frame \(S^\prime \) now need to be established in Frame \(S \). Which gets Special Relativity into even more trouble.
If the same light signal is used to synchronize clocks in Frames \(S \) and \(S^\prime \), the relationships between the speed of the coordinating light signal and the relative speeds of the Frames will remain the same.
Please recall Einstein’s 1905 equations for computing elapsed time as observed from the Frame that is deemed stationary with respect to the stationary system of coordinates.
\(dt\left(downstream\right)=\frac{dx}{c-v} \)
and
\(dt\left(upstream\right)=\frac{dx}{c+v} \)
In our first scenario, Frame \(S^\prime \) was deemed to be moving such that the synchronizing light signal travels in the direction of Frame \(S^\prime \) motion at a speed \(v \) slower (relative to Frame \(S^\prime \)) than the same light signal travels with respect to Frame \(S \), and opposite to the direction of reference Frame \(S^\prime \) motion at speed \(v \) faster (relative to Frame \(S^\prime \)) than the same light signal travels with respect to Frame \(S \).
This fixed relationship has a real-world impact on the clocks of each of the inertial reference frames, and this impact cannot be reversed by changing coordinate systems.
So, by exchanging the numerical values of the “primed” and “unprimed” quantities and by reversing the polarity of \(v \), we cause Frames \(S \) and \(S^\prime \) to exchange their relative speeds with respect to the synchronizing light signal. In other words, we change the physical setup. And this will require the resynchronization of the clocks in both Frames.
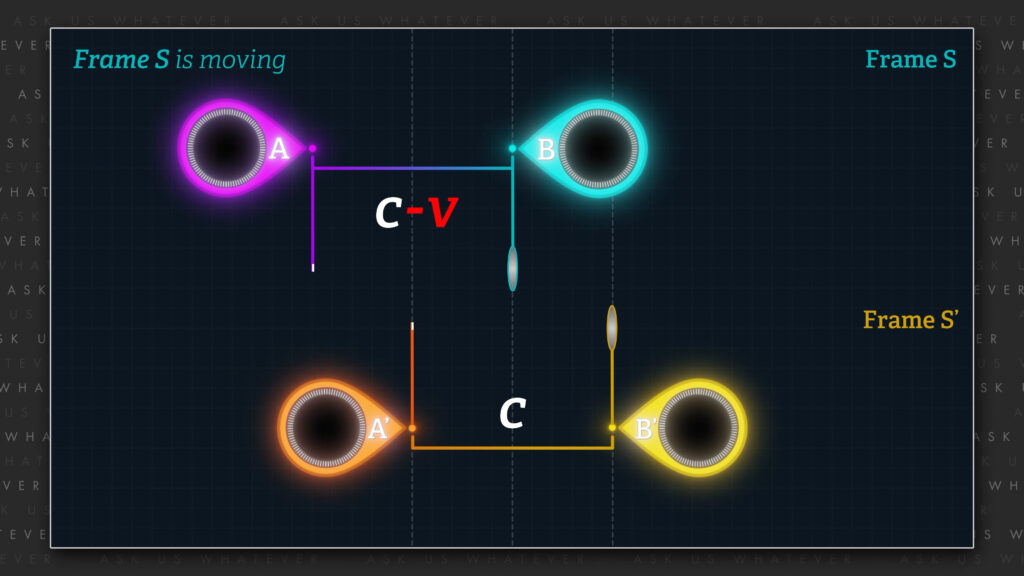
That’s not Relativity, that’s Act 1 and Act 2 of a play!

Einstein incorrectly assumed that the term “\(v \)” was simply the relative speeds of two inertial reference frames, and did not realize that his very own formulas implied a specific, polar relationship between the synchronizing light signal and each frame. His misinterpretation has created a great deal of confusion.
So how do we fix this mess? How do we cause an observer in Frame \(S \) to observe half as much time to elapse in Frame \(S^\prime \) as in Frame \(S \), and vice versa while still holding a straight face?
We will change the behavior of the observers, but we will not change the coordinate systems or the motions of the reference frames relative to those coordinate systems.
We will continue to anchor the stationary system of coordinates to Frame \(S \), and will continue to view Frame \(S^\prime \) as moving with respect to those coordinates. We can still address the principle of relativity from the perspectives of the observers in Frames \(S \)and \(S^\prime \), but we must do so with the understanding that the fundamental measurements of distances, clock rates, and clock readings remain unchanged.
With that in mind, let’s have the Master take readings from two clocks in Frame \(S \). If the Master’s movement in Frame \(S \) tracks a single clock in Frame \(S^\prime \), the offset between clocks in Frame \(S^\prime \) becomes irrelevant. So, the Master will observe the true time elapsed on a single clock in Frame \(S^\prime \) without the distortion associated with the spatial gradient of clock readings in Frame \(S^\prime \).
And since Frame \(S \) is linked to the stationary system of coordinates, meaning that the speed of Frame \(S \) with respect to those coordinates is zero, then clock synchronization in Frame \(S \) produces no clock offset, since the amount of time required for light to travel a distance \(dx \) in either direction in Frame \(S \) is simply equal to \(dx \) divided by \(c \)
\(dt\left(light\ rays\ from\ A\ to\ B\right)=\frac{dx}{c\pm0}=\frac{dx}{c}in\ both\ directions \)
\(no\ need\ for\ \left(c-v\right)\ and\ \left(c+v\right) \)
And so, there is no need to adjust clocks in Frame \(S \) to force light speed to be constant.
Which means that the Master can travel through Frame \(S \) and read from multiple clocks in Frame \(S \), and the differences in clock readings will be due solely to the time elapsed on all of the clocks in Frame \(S \), without any distortions, since there is no clock offset in Frame \(S \).
But in order for the Master to take these clock readings while tracking clock \(A^\prime \), the Master is going to need a rocket pack.
So, let’s set up a meeting between the Master and the Clown in the demilitarized reference frame zone, where the Master borrows the rocket pack from the Clown.

Which means that we can let the Clown take a break and enjoy a cool drink next to clock \(A^\prime \).

So, how far must the Master travel through Frame \(S \) to keep pace with the single clock in Frame \(S^\prime \)?
Well, the Master must fly the distance that one of the Frame \(S^\prime \) clocks moves in 0.58 Frame \(S \) seconds. If Frame \(S^\prime \) moves at about 87% of speed \(c \) for 0.58 seconds, Frame \(S^\prime \) and the clocks within it will have moved, 0.5 light seconds (which is about 150 million meters).
\(dx=v\times dt \)
\( =0.87\times0.58=0.5\ light\ seconds \)
\(=150,000,000\ meters \)
In other words, the Master must fly 150 million meters in Frame \(S \) to keep pace with one of the clocks in Frame \(S^\prime \).
Note that this is not the numerical value of \(dx^\prime \) in the first scenario. That value was 300 million. The distance the Master must move between clocks is not 300 million meters, its 150 million meters, which is the actual physical distance between clocks \(A^\prime \) and \(B^\prime \) in the first scenario. In other words, we are not performing a coordinate system rotation, and we are not changing the setup, nor the distances; we are merely changing the behavior of the observers.
This can also be confirmed with the Lorentz \(dx^\prime \) transformation, provided that we use the new value for \(dx \), which is 0.5 light seconds (150 million meters).
\({dx}^\prime=\gamma_Ldx-\gamma_Lvdt \)
\({dx}^\prime=2\times0.5-2\times0.87c\times0.58 \)
\({dx}^\prime=0 \)
And what, under these new constraints is the value of \(dx^\prime \), which is the time the Master observes elapsing on a single clock in Frame \(S^\prime \)?
\(dt^\prime=\gamma dt-\frac{\gamma vdx}{c^2} \)
\(dt^\prime=2\times dt-\frac{2\times0.87\times0.5}{1^2} \)
\(dt^\prime=2\times0.58-0.87 \)
\(dt^\prime=0.29\ seconds^\prime \)
Well, the Lorentz \(dt^\prime \) transformation shows us that it is 0.29 seconds’ when \(dx \) is 0.5 light seconds. This is the time that elapses on a single Frame \(S^\prime \) clock.
So, the Master measures an elapsed time of 0.58 seconds in Frame S and an elapsed time of 0.29 seconds’ in Frame S’. And so, the Master concludes that half as much time elapsed in Frame S’ as in Frame S.
Which is the result that adherents to Special Relativity want you to learn!
Note, that we did not change the speed of Frames \(S \) or \(S^\prime \) relative to a synchronizing light signal, and thus we did not change the synchronization of clocks or the lengths of measuring tools in Frames \(S \) and \(S^\prime \). We simply changed the actions of the observers.
But, in order to keep the “opposite clock is slower” myth alive, the Clown cannot ask the Master how much time, \(dt \), elapsed in Frame \(S \), since the Master would say 0.58 seconds, and the Clown, now resting next to a single clock in Frame \(S^\prime \), would observe only 0.29 seconds\(^\prime \). And so, the Clown would conclude that twice as much time elapsed in Frame \(S \) as compared to the Clown’s own Frame \(S^\prime \), which is an inconvenient truth that must be ignored by fans of Special Relativity.
What if the Master had taken a personal clock on the trip from clock \(A \) to clock \(B \) while staying aligned with clock \(A^\prime \)? That personal clock would have recorded only 0.29 seconds\(^\prime \) because time dilation would have caused the Master’s personal clock to beat at the same rate as the clocks in Frame \(S^\prime \).
That’s also an inconvenient fact for Special Relativity, and therefore one that’s ignored.
So, by ignoring certain facts and focusing only on others, we’re able to concoct a scenario that’s consistent with the myths of Special Relativity. But we had to use expediency rather than transparency to set up the ground rules for communication.
And so, we return to Dingle’s original objection to Special Relativity and to my claim in Episode 7.1 that if a clock in Frame \(S \) ticks faster than a clock in Frame \(S^\prime \), it is not possible for the clock in Frame \(S^\prime \) to also tick faster than the clock in Frame \(S \). And if you made it this far without falling asleep, I assume you now understand what I was talking about.
Tick rate (or tempo) never changes for clocks that remain at the same location within a non-accelerating inertial reference frame, regardless of whether an observer in Frame \(S \) believes that Frame \(S \) is stationary, or an observer in Frame \(S^\prime \) believes that Frame \(S^\prime \) is stationary. The observers do not telepathically control clock tempo.

Most of the debate between Dingle and his detractors took place in the journal Nature in the 1960s and 1970s. And although Dingle had some of the same misunderstandings as his detractors, and the debate wandered into irrelevant tangents, the editors of Nature cut Dingle off and sided with the detractors. But if the editors had not been so adherent to Einstein and Special Relativity, perhaps the debate could have led to the truth.
Fortunately, for us, we no longer need the scientific establishment to mediate our communications. I can speak to you directly, and you can pick apart my arguments in the comments section. So, have at it! If you see a flaw in what I’ve just said, write it in the comments section. Of course, if you like what you just saw, please let me know. The goal here is to get to the truth.
Alright, I’m Joe Sorge, and thanks for watching.
References
Jonathan Doolin – Is there a solid counter-argument against Dingle’s old objection to Relativity Theory? (Researchgate)
https://www.researchgate.net/publication/352998464_Is_there_a_solid_counter-argument_against_Dingle’s_old_objection_to_Relativity_Theory