Hey! Welcome to Ask Us Whatever. I’m Joe Sorge.
So, we’ve been posting our videos, nicely trying to show that Lorentz and Einstein made some mistakes; and of course, we’ve begun to get some expected blowback.
Here’s an excerpt from a comment from someone called AnticitizenX:

“You seem to be under the naive impression that physicists just postulated this stuff out of nothing. That’s entirely untrue, and it shows that you really haven’t studied this stuff formally. The Lorentz transformation is the only logical way to satisfy basic assumptions about motion and time… I hate to break this to you, but your entire video series is the logical equivalent to an argument that 2+2=5.”
Hah! OK, you succeeded in getting my attention! And you know, I was once at a comedy show by the late Sam Kinison, and there was a heckler in the audience. And Sam said, “You know the last thing in the world you wanna do is get my attention.”
Well, it turns out that I had read several derivations of your beloved longitudinal Lorentz transformations prior to making these videos, and I did just now read what I presume is your paper on the subject, posted in 2015. So, let’s get into it!
But first, I must apologize to our viewers, I haven’t covered the longitudinal Lorentz transformations yet. So, if you don’t want to watch me skewer the Lorentz transformations using a very technical (I mean mathematical) approach, it’s ok to skip to the next episode, where we’ll take it a little more slowly and less intensely. But if you’d like to see a chapter from the bible of physics go up in flames right in front of your eyes, then please enjoy the next few minutes.
Alright, so I hope you enjoy the rest of this video where we set a chapter from the bible of physics up in flames.
Alright, most of the derivations of the longitudinal Lorentz transformations go like this.
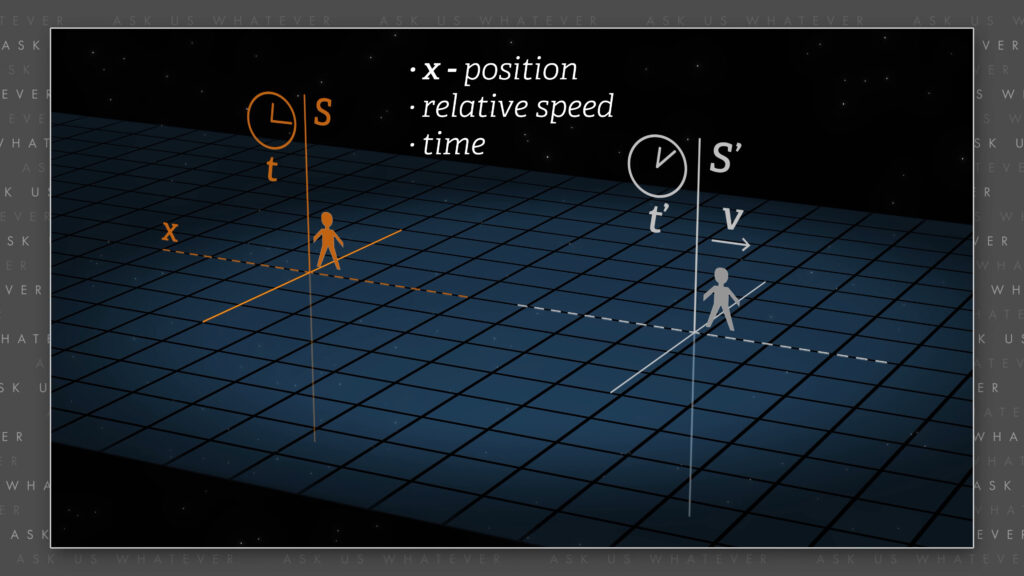
There are two inertial frames of reference, let’s call them \(S \) and \(S^\prime \) moving relative to one another along the \(x \)-axis. We assume that observers in the two frames see things a bit differently, but that we can transform their position and time coordinates into those observed by those in the other frame, by tracking \(x \)-position, relative speed, and time in both systems. The Lorentzians believe that these transformations take on a general form,
\(dx=Adx^\prime+Bdt^\prime \)
\(dt=Cdt^\prime+Ddx^\prime \)
whereby, the change in position of an object (or light ray) along the \(x \)-axis in the \(S \) frame, \(dx \), equals a variable \(A \) times the change in position along the \(x^\prime \)-axis in the \(S^\prime \) frame, \(dx^\prime \), plus a variable \(B \) times the change in time in the \(S^\prime \) frame, \(dt^\prime \).
And the change in time \(dt \) in the \(S \) frame is equal to the variable \(C \) times the change in time in the \(S^\prime \) frame, \(dt^\prime \), plus a variable \(D \) times the change in position along the \(x^\prime \)-axis in the \(S^\prime \) frame.
The goal is to then solve for variables \(A \), \(B \), \(C \), and \(D \), assuming that the variables depend only on \(x \) or \(x^\prime \)-position, \(v \) or \(v^\prime \) speed, and \(t \) or \(t^\prime \)-time so that one can predict \(x \), \(v \), and \(t \) from \(x^\prime \), \(v^\prime \), and \(t^\prime \), and vice versa.
Before we start the derivation, it’s important to review the way measurements are made in special relativity in the \(S^\prime \) frame. As we pointed out in Episode 5, even though lengths in the \(S^\prime \) frame are presumed to contract along the x-axis, the observers in \(S^\prime \) are presumed to not notice because their measuring devices also contract proportionally. I know, that sounds like circular logic; and it is. But that’s one of the basic assumptions made by Lorentz and Einstein.
We also learned in Episode 2 that clocks may need to be offset to different readings in order for events to appear to happen simultaneously in the \(S^\prime \) frame.
For light, we call the process that creates these offsets in time, Einstein synchronization, which means that the time between events in \(S^\prime \) is measured with clocks that not only beat in time-dilated seconds\(^\prime \), but that also have been adjusted to read differently at different locations.
So \(dt^\prime \) does not represent the number of seconds\(^\prime \) that elapse between events that occur at different locations in \(S^\prime \). Instead, it represents the number of seconds\(^\prime \) elapsed, as further modified by the difference in clock settings between the starting clock and the ending clock.
As covered in Episode 3, I believe that time dilation is caused by the speed at which a clocks move relative to electromagnetic radiation—a natural process. But in contrast, please recognize that Einstein synchronization is due to human intervention.
Someone, or some process, must adjust the clock readings so that events that are not simultaneous in the \(S \) frame might appear to be simultaneous in the \(S^\prime \) frame. If the setup changes—for example the moving frame changes speed—some process needs to be carried out to essentially manually adjust the clocks so that they report in a format compatible with the Lorentz transformations. The clocks don’t adjust themselves automatically; and if one were to take readings from the unadjusted clocks, the Lorentz transformations would produce erroneous results.
So that should raise your level of skepticism: Einstein synchronization, not nature, causes clocks to be adjusted so that light appears to be moving at a constant speed, and so that the principle of relativity appears symmetric. Without that manual intervention, Einstein’s postulates fall apart.
Now, armed with these weird clocks, the typical first step in the derivation of the Lorentz transformations is to set \(dx^\prime \) (which, recall, is the distance that an observer in the “moving frame” moves within the moving frame) to zero, and then to solve for \(\frac{dx}{dt} \),
\(dx=Adx^\prime+Bdt^\prime \)
\(dt=Cdt^\prime+Ddx^\prime \)
\(dx=A\cdot0+Bdt^\prime \)
\(dt=Cdt^\prime+D\cdot0 \)
\(dx=Bdt^\prime \)
\(dt=Cdt^\prime \)
\(\frac{dx}{dt}=\frac{Bdt^\prime}{Cdt^\prime}=\frac{B}{C} = v \) (when \(dx^\prime = 0\))
The change in \(x \) divided by the change in \(t \) is equal to \(B \) times \(dt^\prime \) divided by \(C \) times \(dt^\prime \), which is equal to \(B \) divided by \(C \). Since \(dx^\prime \) is zero, meaning an observer in the \(S^\prime \) frame does not move along the \(x^\prime \) axis, that observer has zero \(\frac{dx^\prime}{dt^\prime} \) speed. But when viewed from the stationary frame, that observer is moving in space because their frame \(S^\prime \) is moving, so \(\frac{dx}{dt} \) is equal to the speed of the \(S^\prime \) frame, which we call \(v \). If the observer were to move around within the \(S^\prime \) frame, \(\frac{dx}{dt} \) would have to factor in the observer’s \(\frac{dx^\prime}{dt^\prime} \) speed as well. But for this first step, \(dx^\prime \) and \(\frac{dx^\prime}{dt^\prime} \) are zero.
We measure \(v \), the speed of moving frame \(S^\prime \) in units of meters per second, since stationary observers measure \(v \) with clocks in the “stationary frame”. Since the speed of the moving frame, \(v \), is independent of the speed of objects or observers within the moving frame, we may conclude that,
\(B=C \frac{dx}{dt}=Cv \)
\(B \) equals \(C \) times \(v \), regardless of whether \(dx^\prime \) is zero or not. Careful to note that this is capital \(C \), a variable, not light speed \(c \).
So, we can rewrite the two transformations as,
\(dx=Adx^\prime+Cvdt^\prime \)
\(dt=Cdt^\prime+Ddx^\prime \)
\(dx \) equals \(A \) times \(dx^\prime \) plus \(C \) times \(v \) times \(dt^\prime \); and \(dt \) equals \(C \) times \(dt^\prime \) plus \(D \) times \(dx^\prime \). So far, so good. I agree with the logic until now.
However, here’s where the Lorentzians make a big assumption that’s not justified on its face. They will typically set \(dx \) to zero, which means that events occur at a specific location in the stationary frame,
\(0=Adx^\prime+Cvdt^\prime \)
and then write the equation \(A \) times \(dx^\prime \) plus \(C \) times \(v \) times \(dt^\prime \) to equal zero. This equation can be rearranged to yield,
\(\frac{dx^\prime}{dt^\prime}=\frac{-Cv}{A} \)
the change in \(x^\prime \) with respect to the change in \(t^\prime \) equals negative \(C \) divided by \(A \) times \(v \).
The unsupportable assumption that the equal-speed Lorentzians make is to wrongly assume that \(\frac{dx^\prime}{dt^\prime} \) must equal \(-v \) when \(dx \) is equal to zero. In other words, if an object within frame \(S^\prime \) is moving at speed \(\frac{dx^\prime}{dt^\prime} \) meters per second\(^\prime \), but that object appears to be stationary from the perspective of frame \(S \) (that is, \(dx \) equals zero), the Lorentzians wrongly conclude that capital \(C \) must equal capital \(A \), so that capital \(C \) divided by capital \(A \) is \(1 \),
\(\frac{dx^\prime}{dt^\prime}=\frac{-Cv}{A}=-1\cdot v \)
and that
\(\frac{dx^\prime}{dt^\prime} = -v \)
\(\frac{dx^\prime}{dt^\prime} \) is equal to negative \(v \).
To help illustrate their logic, picture a clown walking backwards on a moving walkway in an airport, at the same speed as the walkway moves forward.
The people in the hallway, laughing at the clown, will see him as stationary with respect to the hallway. In other words, \(dx \) equals zero even though \(\frac{dx^\prime}{dt^\prime} \) and \(v \) are both non-zero.
\(\frac{dx^\prime}{dt^\prime} \) meters/second\(^\prime \neq-v \) meters/second
But think about it, \(\frac{dx^\prime}{dt^\prime} \) is measured in meters per second\(^\prime \) in frame \(S^\prime \) and speed \(v \) is measured in meters per second as seen from frame \(S \). This should immediately hoist a huge red flag 🚩. One of the lynchpins of special relativity as you know, is that clocks will tick at different rates when moving at different speeds.
The clocks in frame \(S^\prime \) are moving along with the moving walkway. They tick slower than the clocks in the hallway, and their tick rate is measured in units of seconds\(^\prime \).
The stationary observers in the hallway measure the speed of the moving walkway, \(v \), using the stationary clocks hanging on the walls of the hallway.
Those clocks tick faster than the clocks associated with the moving walkway, and they measure time in units of seconds, which are of shorter duration than seconds\(^\prime \). And so, when these two sets of observers compute speeds, they will be doing so using different units of time. Therefore, if the clown appears stationary to the observers in the hallway, then\(\frac{dx^\prime}{dt^\prime} \) meters per second\(^\prime \)
\(\frac{dx^\prime}{dt^\prime} \) \(^\prime \)meters/second\(^\prime\neq-v \) meters/second
cannot equal \(-v \) meters per second unless something more complex is going on, which it is. So, let’s find it.
AnticitizenX wrote another comment to Episode 6.1 and suggested that I look up, “Getting the Lorentz transformations without requiring an invariant speed.”
So, I searched for the title and found an article by Andrea Pelisseto and Massimo Testa online.
The approach in their paper, like many papers on special relativity, is mathematically elegant, but, again, conceptually flawed.
They point out that in the \(S \) from \(S’ \) distance and time transformations that the variable \(C \) is associated with the proper time \(dt^\prime \).
\(dx=Adx^\prime+Cvdt^\prime \)
\(dt=Cdt^\prime+Ddx^\prime \)
In fact, when \(dx^\prime=0 \) in the original time transformation,
(When \(dx^\prime=0 \)) \(dt=Cdt^\prime \)
\(dt \) equals \(C \) times \(dt^\prime \), which by definition makes capital \(C \) a time-dilation factor, which the Lorentzians typically call gamma,
\(C=\gamma \)
(When \(dx^\prime=0 \)) \(dt=\gamma dt^\prime \)
Now the Lorentz transformations not only purport to provide equations for determining the time and location of an observer in a second reference frame as measured from a first frame, but they also purport to provide the symmetrical inverse, whereby an observer in the second reference frame can determine the time and location of an observer in the first frame.
Pelisetto and Testa begin their derivation by applying Cramer’s rule to derive these inverse equations using matrices and determinants. I think this is an elegant approach. If you do not know Cramer’s rule, please search for it online. There are many good descriptions.
By applying Cramer’s rule to the \(S \) from \(S^\prime \) transformations, in which variable \(C \) is replaced with gamma, \(B \) is replaced with gamma times \(v \), and in which we just change the order of terms in the second equation, we can begin to derive the inverse transformations:
\(S \) from \(S^\prime \) Transformations
\(dx=Adx^\prime+\gamma vdt^\prime \)
\(dt=Ddx^\prime+\gamma dt^\prime \)
You can see the logic for deriving these inverse transformations here:

\(S^\prime \) from \(S \) Inverse Transformations
\(dx^\prime=\frac{\gamma dx-\gamma vdt}{A\gamma-\gamma vD}=\frac{dx-vdt}{A-vD} \)
\(dt^\prime=\frac{Adt-Ddx)}{\gamma(A-vD)} \)
Again, please review Cramer’s rule on line if this went too fast for comfort. It’s an elegant method and well worth knowing.
But then Pelisetto and Testa apply the questionable logic of most Lorentzian derivations, and equate \(\frac{dx^\prime}{dt^\prime} \) with \(-v \), leading them to conclude that \(A \) equals \(C \). Which means that they then will rewrite the transformations as,

\(S \) from \(S^\prime \) Transformations
\(dx=\gamma dx^\prime+\gamma vdt^\prime \)
\(dt=Ddx^\prime+\gamma dt^\prime \)
\(S^\prime \) from \(S \) Inverse Transformations
\(dx^\prime=\frac{dx-vdt}{\gamma-vD} \)
\(dt^\prime=\frac{\gamma dt-Ddx}{\gamma(\gamma-vD)} \)
You can pause the video to study them.
Pelisetto and Testa, after deriving their formulas for \(dt \) and \(dt^\prime \) which explicitly show that \(dt \) does not simply equal \(dt^\prime \), and \(dt^\prime \) does not simply equal \(dt \), they then propose that \(dt \) equals \(dt^\prime \)!
What?! Where does that come from?! But that erroneous assumption will lead to the erroneous Lorentz transformations. Somehow Lorentzians convince themselves that clock A can be slower than clock B, AND clock B can be slower than clock A, AND that both clocks can also tick at the same rate, all concurrently and all in the same setup. No, it’s not like two distant observers seeing each other as smaller than themselves. That’s a simple phenomenon related to distance and light rays, but not time. The Lorentz transformations rely on clocks, which requires an exquisite appreciation of time dilation to understand fully. And since you’ve been watching this video series, you have that exquisite appreciation!
Pelisetto and Testa also bring mathematical group theory into their derivation and try to eliminate the typical reliance on assuming a constant light speed. But the group theory they refer to assumes a symmetry that’s not there! That symmetry may be useful in pure mathematics, but it does not apply to real world clocks.
Unfortunately, this logic led Pelisetto and Testa to conclude that the value of Cramer’s determinant
\(\gamma(\gamma-vD)=1 \)
is 1, which led them to erroneously conclude that \(A \) and \(C \) equal the Lorentz gamma factor, and that \(D \) is equal to the Lorentz gamma factor times \(v \) divided by \(c \) squared.
\(dx=\gamma dx^\prime+\gamma vdt^\prime \)
\(dt=\frac{\gamma v}{c^2} dx^\prime+\gamma dt^\prime \)
\(dx^\prime=\gamma dx-\gamma vdt \)
\(dt^\prime=\gamma dt- \frac{\gamma v}{c^2} dx \)
You can pause the video here to confirm that these are the standard Lorentz transformations.
Let’s confirm the formula for capital \(D \) and, while we’re at it, capital \(A \), using a different path of logic. Special relativity relies on the assumption that lengths contract in the moving frame, and that this can be seen from the stationary frame. Which means that when \(dt \) equals zero,
(When \(dt=0 \)) \(dx^\prime=\gamma dx \)
the numerical value of \(dx^\prime \), as measured with contracted meter sticks by observers in the moving frame \(S^\prime \), will be greater than the corresponding numerical value \(dx \), as measured with normal meter sticks from the stationary frame, by a factor of gamma. Earlier we found the general formula for \(dx^\prime \) using Cramer’s rule to be,
\(dx^\prime=\frac{Adx-\gamma vdt}{\gamma(A-vD)} \)
capital \(A \) times \(dx \) minus gamma times \(v \) times \(dt \), all divided by gamma times the quantity, capital \(A \) minus \(v \) times capital \(D \). When \(dt = 0 \), this simplifies to
(When \(dt=0 \)) \(dx^\prime=\frac{Adx}{\gamma(A-vD)} \)
capital \(A \) times \(dx \) divided by gamma times the quantity, capital \(A \) minus \(v \) times capital \(D \). This formula will satisfy special relativity’s length contraction requirement,
(When \(dt=0 \)) \(dx^\prime=\gamma dx \)
when both capital \(A \) equals gamma,
(When \(dt=0 \)) \(dx^\prime=\frac{\gamma dx}{\gamma(\gamma-vD)} =\frac{\gamma dx}{1} \)
and the denominator equals \(1 \). So, provided we can find a value of \(D \) such that the denominator is equal to \(1 \), we can satisfy the length contraction requirement of special relativity. If we plug in Lorentz’s formula for gamma into the equation,
\(\gamma(\gamma-vD)=1 \)
gamma times the quantity gamma minus \(v \) times capital \(D \), and then use some fast algebra to solve for \(D \), we find that,
\(D=\frac{\gamma v}{c^2} \)
capital \(D \) equals gamma times \(v \) divided by \(c \) squared.
You might be wondering, if they made the unsupportable assumption that \(\frac{dx^\prime}{dt^\prime} \) equals \(-v \), then how do these equations reconcile the dimensional unit mismatch between the \(S \) frame and the \(S^\prime \) frame? It’s a real mismatch and it creates a real error if not fixed! Well, the capital \(D \) term fixes it.
The capital \(D \) term in the Lorentz derivation is,
\(D=\frac{\gamma v}{c^2} \)
gamma times \(v \) divided by \(c \)-squared.
It can be referred to as the clock-offset term, and it’s the result of the manual Einstein clock synchronization I referred to earlier. Again, it’s not something that occurs naturally; it requires human intervention. The degree of clock adjustment changes with the speed difference between reference frames, so it must be carried out differently for each pair of reference, which creates an impossible conflict in logic as we will see in a few minutes.
So let’s explore how Einstein clock synchronization works.
If you recall in Episode 2 we talked about clock synchronization, with a drummer, a singer, and a guitarist on a train. Now, there we didn’t explicitly derive the capital \(D \) term in that episode, but for sound waves it would equal,
\(t_{drummer}-t_{guitarist}=\frac{1}{2}(\frac{dx^\prime}{c-v}-\frac{dx^\prime}{c+v})\)
\(=\frac{vdx^\prime}{c^2 -v^2}=\frac{\gamma^2 v}{c^2}dx^\prime \)
gamma squared times \(v \) divided by \(c \)-squared, where \(c \) is the speed of sound in air.
Notice that for sound waves, the analog of capital \(D \) contains a gamma-squared term. However, Einstein claimed that light is different, and that the fantasies of special relativity allow one to contract lengths by a factor of gamma, which allows the capital \(D \) term to be contracted by one factor of gamma, yielding a capital \(D \) term of:
\(t_{front}-t_{rear}=\frac{1}{2}(\frac{dx^\prime}{\gamma (c-v)}-\frac{dx^\prime}{\gamma (c+v)}) \)
\(=\frac{\gamma vdx^\prime}{\gamma^2(c^2 -v^2)}=\frac{\gamma v}{c^2}dx^\prime \)
gamma times \(v \) divided by \(c \)-squared. That’s what you get when you perform Einstein synchronization on a contracted length.
In other words, you have to adjust the readings on clocks depending on where they lie along the \(x^\prime \) axis. Clocks that lie in the positive \(x^\prime \) direction, that is, in the direction of reference frame motion, must be set to an earlier time reading than clocks that lie away from the direction of reference frame motion. Textbooks on special relativity that talk about clocks at the rear of a moving train car being set ahead of a clock at the front of a moving train car.
If such adjustments are made to the clocks, the Lorentzians can then equate \(\frac{dx^\prime}{dt^\prime} \) meters per weirdly adjusted second\(^\prime \) with \(-v \) meters per stationary second, provided that their clocks are offset by capital \(D \) times \(dx^\prime \). We’ll save the math behind this statement for our future episode on relativistic velocity addition, but in words, when \(dx = 0 \), the clock offset term perfectly balances the difference between the reading on the clown’s personal clock with the readings on the Einstein-synchronized moving walkway clocks.
This means that the observers in the hallway must see the clocks that are riding along on a length-contracted moving walkway, to report different times depending on the clocks’ length-contracted positions along the walkway, and the clown must use these screwy, Einstein-synchronized clocks to compute his elapsed time, as denominated in meters per second’. Otherwise, he will not find that the numerical value of \(\frac{dx^\prime}{dt^\prime} \) meters per screwy seconds\(^\prime \) is equal to the negative \(v \) meters per second speed of the moving walkway.
Now, Lorentzians will argue that although the clocks have been rigged to give the desired results, such results reflect what observers actually experience within each reference frame. But I don’t agree that this is valid, because the theory creates some irreconcilable conflicts. Let’s explore those:
The clown is moving relative to the clocks on the moving walkway in frame \(S^\prime \). According to special relativity, his clock should beat slower than the clocks on the moving walkway, because from the perspective of those clocks, the clown is the one who is moving relative to frame \(S^\prime \). But the math of the Lorentz transformations requires that the clown’s clock beat at the same rate as the stationary clocks on the walls of the hallway, which beat faster than the clocks on the moving walkway, not slower than the moving walkway clocks. So, there is an irreconcilable conflict.
And here’s the one that really nails it, if there are two moving walkways in the airport hallway, each moving at different speeds, then the hallway wall clocks must be Einstein-synchronized differently for each moving walkway! If the principle of relativity is truly symmetric, as special relativity claims, and there is no preferred frame of reference, then Einstein synchronization must be unique for each pair of moving clocks; hallway clocks moving relative to walkway 1; and hallway clocks moving at a different speed relative to walkway 2.
So, what happens when people on the different walkways look at the same wall clocks? How would Einstein slow them down to offset their times differentially to suit the requirements of each set of moving-walkway observers? The answer is he can’t! I’m sorry Anticitizen X, but special relativity and the Lorentz transformations require unique physical objects to be in multiple, conflicting configurations at the same time.
And if that impossibility isn’t devastating enough, consider this: in the frame of reference of the moving walkway clocks, special relativity requires the clown’s distance traveled and the airport hallway to both contract, even though the clown is still in frame \(S^\prime \), which now needs to expand. So, the clown must walk a contracted distance on a walkway that just got longer!
It all appears to me like a bass-ackwards, convoluted, and mutually inconsistent way of making observations and computing speeds. I’m sorry, but Lorentz should get an F, and if Einstein looked over Lorentz’s shoulder at exam time, then he should go stand at the back of the room and face the wall.
So, why would Einstein and Lorentz conjure up such a convoluted way of computing distances and times? Well, it was the only way that they could think of to preserve the speed of light to be c in all frames of reference while remaining consistent with the Michelson Morley result. But it required them to propose that lengths magically contract and that clocks that would otherwise be offset by a gamma-squared term when measuring the speed of sound waves would only be offset by a gamma term while measuring the speed of light waves. And so, physics took a turn toward fantasy land. Well, we’re not going to head down the same path. Instead, we are going to re-derive the time and distance transformations, while staying grounded in reality.
So, in the next episode we’ll derive those transformations, and then we will begin to rewrite the relativistic Doppler equations, explain stellar aberration, rescind the universal speed limit, and possibly revise the thinking about stellar red shifts.
Alright, if you have any questions, please write them in the comments section. I’m Joe Sorge, and thanks for watching.
Further Reading
NIH: Relativity in the Global Positioning System
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5253894/



