In Episode 9.1 we learned about relativistic velocity addition according to the Special Theory of Relativity. And although the textbook formula is simple, the details behind the formula reveal its dependence on length contraction and Einstein-synchronized clocks. And since these lengths and clocks must be adjusted for each observer, the conflicting constraints that would be imposed by multiple observers in multiple reference frames makes the velocity addition formula, and the underlying Special Theory of Relativity, unworkable.
To bring some reality to velocity addition, we are going to derive the Alternative Model velocity addition formula, and base it on velocities with respect to a Preferred Reference Frame.
We’ll first start with two reference frames. Using the alternative \(dx \) and \(dt \) transformations that you’ve seen in earlier episodes, and then we’ll expand the analysis to multiple reference frames.
\(dx=\gamma_s^2dx^\prime+\gamma_svdt^\prime \)
\(dt=\gamma_sdt^\prime+\frac{vdx^\prime}{c^2} \)
\(\gamma_s \) is computed using the speed, \(v \), of a given moving Frame relative to our Preferred Reference Frame \(S \), as measured in Frame \(S \) meters per second.
\(\gamma_s=\sqrt{1+\frac{v^2}{c^2}} \)
The distance \(dx^\prime \) is how far an object or observer in Frame \(S^\prime \) moves between events within Frame \(S^\prime \). Recall that meter sticks in the Alternative Model do not contract. So, a meter\(^\prime \) is a meter and a meter is a meter.
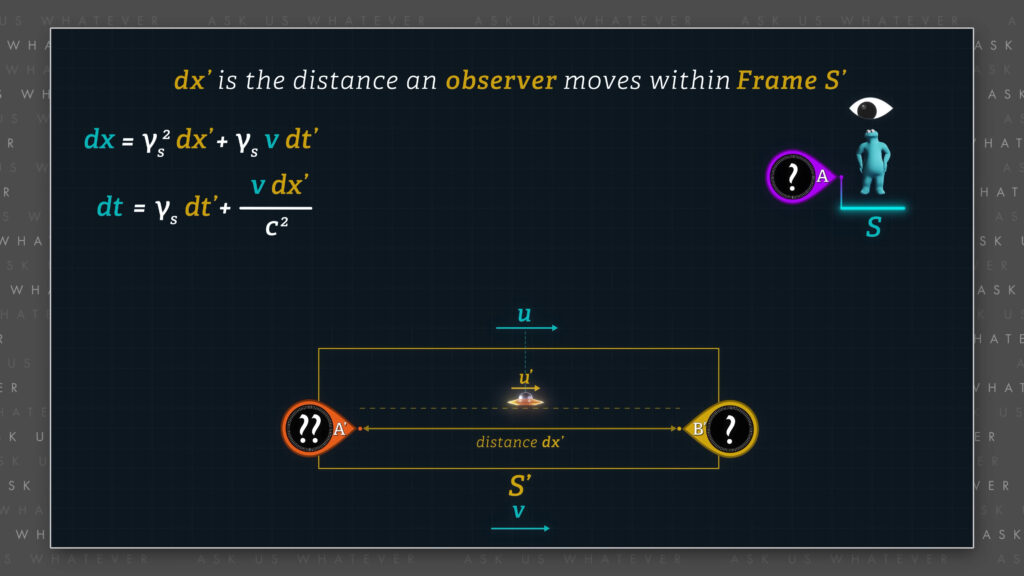
\(dt^\prime \) is the time that elapses while the object or observer moves distance \(dx^\prime \) within Frame \(S^\prime \), as measured with two Frame-\(S^\prime \) clocks separated by that distance \(dx^\prime \).
Note that the two clocks in Frame \(S^\prime \) are Einstein-synchronized, which means that Clock \(B^\prime \) will report an earlier “time of day” than Clock \(A^\prime \). Therefore, the computation of elapsed time \(dt^\prime \) will be affected not only by the time-dilated tempo of Clocks \(A^\prime \) and \(B^\prime \), but also by the difference between the readings being displayed by Clocks \(A^\prime \) and \(B^\prime \).
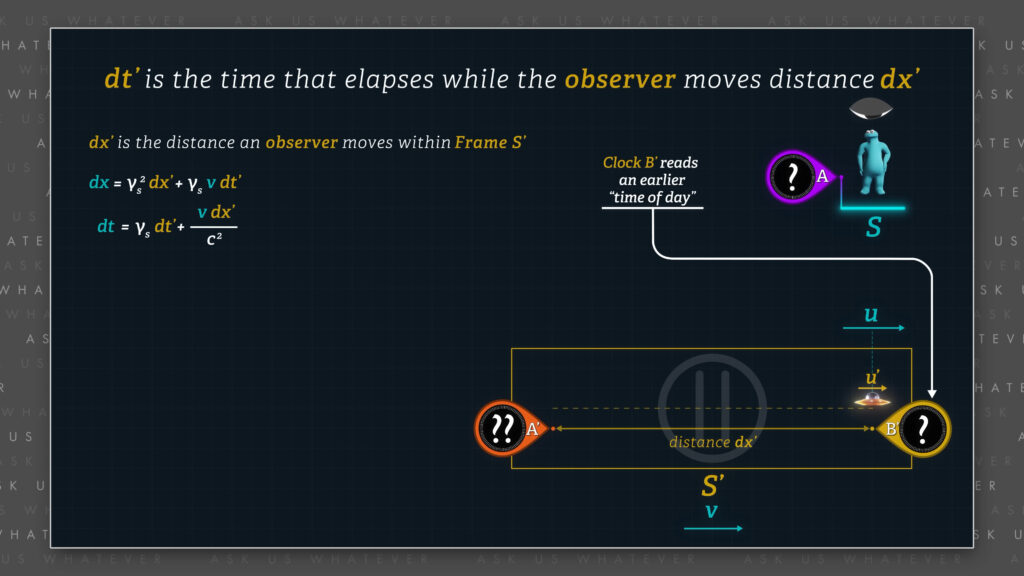
Since clock-offset amounts are computed using reference frame speed relative to a universal, preferred reference frame, clocks will not need to be re-adjusted for different observers, as must be done for Special Relativity. If this does not make sense, please watch Episode 7.2 for an explanation.
The speed of an observer who is moving within Frame \(S^\prime\), as observed and measured from Frame \(S\), is then computed by dividing the alternative \(dx \)-transformation by the alternative \(dt \)-transformation.
\(\frac{dx}{dt}=\frac{\gamma_s^2dx^\prime+\gamma_svdt^\prime}{\gamma_sdt^\prime+\frac{vdx^\prime}{c^2}}\ \ \ \ \ \ \ \ \ \ \ \frac{dx}{dt}=u \)
\(u=\frac{\gamma_s^2dx^\prime+\gamma_svdt^\prime}{\gamma_sdt^\prime+\frac{vdx^\prime}{c^2}} \)
For simplicity we will call speed \(\frac{dx}{dt} \), \(u\). If we divide numerator and denominator by \(\gamma_s \) times \(dt^\prime \) we get the following…
\(u=\frac{\frac{\gamma_s^2dx^\prime}{\gamma_sdt^\prime}+\frac{\gamma_svdt^\prime}{\gamma_sdt\prime}}{\frac{\gamma_sdt^\prime}{\gamma_sdt^\prime}+\frac{vdx^\prime}{c^2\gamma_sdt^\prime}} \)
\(=\frac{\frac{\gamma_s^2dx^\prime}{\gamma_sdt^\prime}+\frac{\gamma_svdt^\prime}{\gamma_sdt^\prime}}{\frac{\gamma_sdt^\prime}{\gamma_sdt^\prime}+\frac{vdx^\prime}{c^2\gamma_sdt^\prime}} \)
\(u=\frac{\gamma_s\frac{dx^\prime}{dt^\prime}+v}{1+\frac{v(\frac{dx^\prime}{dt^\prime})}{\gamma_sc^2}} \)
The speed \(\frac{dx^\prime}{dt^\prime} \) is the speed of the object or observer relative to Frame \(S^\prime \) as measured in meters per second\(^\prime \). Let’s call that speed, \(u^\prime \).
We then have speed \(u \) being equal to \(\gamma_s \) times \(u^\prime \) plus \(v \) all divided by \(1 \) plus \(v \) times \(u^\prime \) over \(\gamma_s \) times \(c \)-squared.
This formula resembles the relativistic velocity addition formula from Special Relativity, except for the \(\gamma_s \) factors. It allows us to compute the speed, \(u \), of a Frame \(S^\prime \) object or observer relative to Frame \(S \).
We can rearrange the formula to find the speed of the Frame \(S^\prime \) object or observer, \(u^\prime \), as observed from within Frame \(S^\prime \), provided that we know the speed \(v \) of Frame \(S^\prime \), and the speed of the object or observer, \(u \) with respect to Frame \(S \).
\(u^\prime=\frac{u-v}{\gamma_s-\frac{uv}{\gamma_sc^2}} \)
\(u^\prime \) is equal to \(u \) minus \(v \) all divided by \(\gamma_s \) minus \(u \) times \(v \) over \(\gamma_s \) times c-squared.
Note that both \(u \) and \(v \) are measured using a single clock in Frame \(S \), and so this formula does not require the synchronization of Clocks in Frame \(S \).
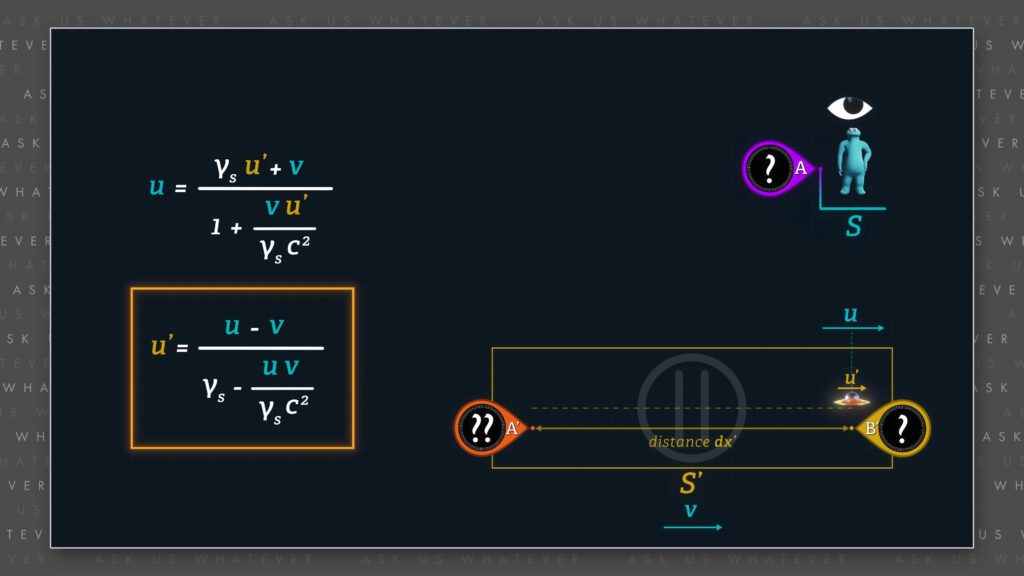
However, the output of this formula, \(u^\prime \), if actually measured in Frame \(S^\prime \) would involve two Einstein-synchronized clocks in Frame \(S^\prime \). This is because the Alternative \(dt \) and \(dt^\prime \) transformations assume synchronized clocks in Frame \(S^\prime \), as do the \(dt \) and \(dt^\prime \) transformations in Special Relativity.

We could write the \(dt \) and \(dt^\prime \) transformations assuming absolutely synchronized clocks in Frame \(S^\prime \) but that’s for a future episode.
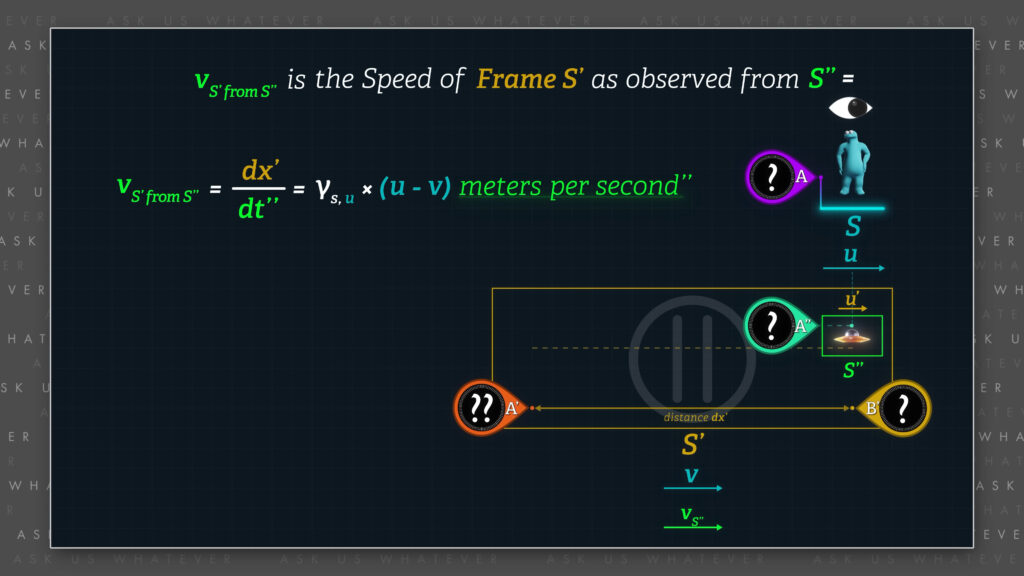
There’s another formula that will become handy when we begin to look at symmetries between multiple frames. Let’s assume that a frame that we call Frame \(S^{\prime\prime} \) (or some object within Frame \(S^\prime\)) moves at speed \(u \) with respect to Frame \(S \), then its speed relative to Frame \(S^\prime\), denominated in Frame \(S \) meters per second, can be computed by simply subtracting \(v \) from \(u \).
Speed of Frame \(S^{\prime\prime} \) relative to \(S^\prime \) (in Frame \(S \) meters per second) \(=\frac{dx^\prime}{dt}=u-v \)
This speed is the distance that \(S^{\prime\prime} \) (or an object moving within Frame \(S^{\prime} \)) moves with respect to Frame \(S^{\prime} \) divided by elapsed time measured with clocks in Frame \(S \).
If we are interested in the speed at which observers in Frame \(S^{\prime\prime} \) observe Frame \(S^\prime \) to be moving, we need to convert \(dt \) to \(dt^{\prime\prime} \).
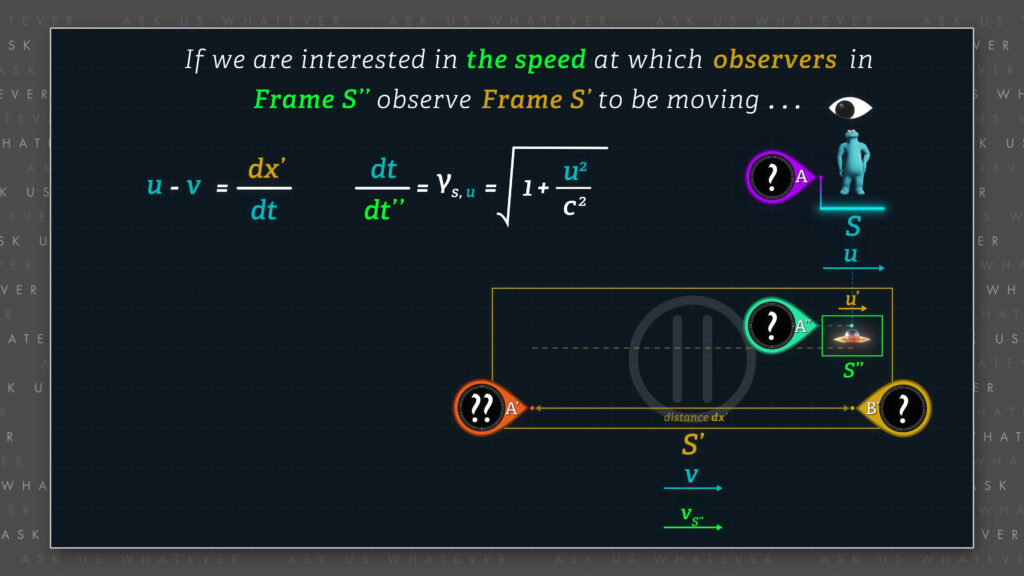
If we use only one clock in Frame \(S \) and one clock in Frame \(S^{\prime\prime} \), the time dilation factor between Frames \(S \) and \(S^{\prime\prime} \) will be equal to \(\gamma_s \) computed using their relative speeds, \(u\).
\(\frac{dt}{dt^{\prime\prime}}=\gamma_{s,u}=\sqrt{1+\frac{u^2}{c^2}} \)
And so, the speed difference between Frames \(S^{\prime\prime} \) and \(S^{\prime} \), as measured by observers who are stationary within Frame \(S^{\prime\prime} \), is, \(\gamma_{s,u} \) times \(u \) minus \(v \) meters per second\(^{\prime\prime} \).
\(u^\prime \) (speed of Frame \(S^\prime \) observed from \(S^{\prime\prime} \)) \(= \frac{dx^\prime}{dt^{\prime\prime}} \)
\(=\gamma_{s,u}\left(u-v\right)\ meters\ per\ second^{\prime\prime} \)
OK, that lays the groundwork for velocity addition in the Alternative Model. In the next episode we will generalize the concepts so that we can compute relative velocities between multiple objects in multiple reference frames.
So, if you have any questions, please write them in the comments section. I’m Joe Sorge, and thanks for watching.



